Показательные неравенства

Показательные неравенства
Определение
Простейшие неравенства
Решение неравенств

Определение
Показательные неравенства –
это неравенства, в которых неизвестное содержится в показателе степени.
Примеры:

Простейшие показательные неравенства – это неравенства вида:
где a > 0, a ≠ 1, b – любое число.

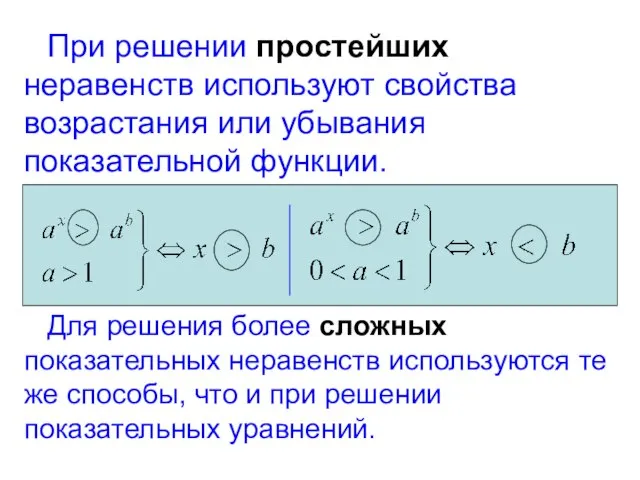
При решении простейших неравенств используют свойства возрастания или убывания показательной функции. Для решения более сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.

Простейшие показательные неравенства
Двойные неравенства
Неравенства, решаемые вынесением за скобки степени с меньшим показателем
Неравенства, решаемые заменой переменной
Решение показательных неравенств

Простейшие
показательные неравенства

Двойные неравенства
Ответ: (- 4; -1).
3 > 1, то

Решение
показательных неравенств
Метод: Вынесение за скобки степени с меньшим
показателем
Ответ: х >3
Т.к.
3 > 1, то знак неравенства остается прежним
: 10