Содержание
- 2. Немецкий ученый, математик, создатель теории множеств Родился в Петербурге в 1845г. В 1867 г. окончил Берлинский
- 3. Цели: 1) описать способы хранения информации о принадлежности элемента множеству, 2) описать алгоритмы для вычисления результатов
- 4. Один и тот же объект может быть представлен разными способами. Выбор представления зависит от многих факторов:
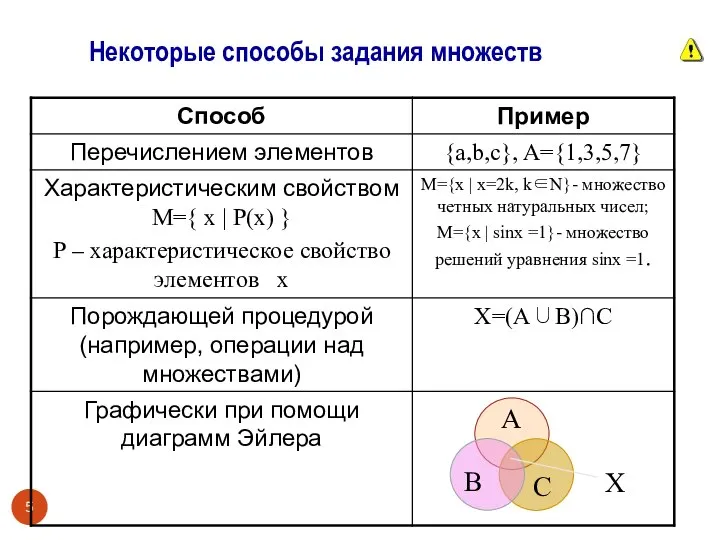
- 5. Некоторые способы задания множеств
- 6. Булеан – множество всех подмножеств данного множества M Обозначение: B(M) Пример: дано множество A={a,b,c}. Найти В(А).
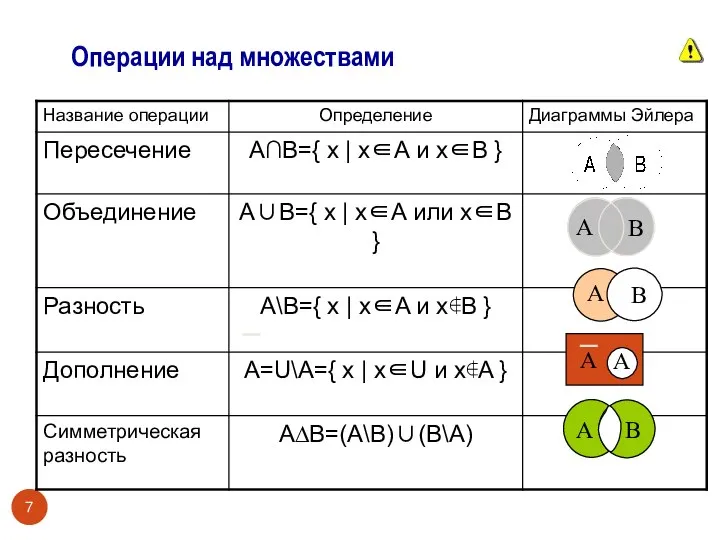
- 7. Операции над множествами А В A B A A A B
- 8. Представление множества машинным словом или битовой шкалой Пусть универсальное множество конечно и число п его элементов
- 9. Если универсум очень велик или бесконечен, а рассматриваемые подмножества не очень велики, то представление с помощью
- 10. Множества будем хранить как массив с нумерацией элементов, начинающейся с единицы. Обозначим через i номер текущего
- 11. Положить i = j = 1 и k = 0. Если в A и B (одновременно)
- 12. Алгоритм нахождения объединения слиянием Обозначим через i номер текущего рассматриваемого элемента в множестве A, через j
- 14. Скачать презентацию









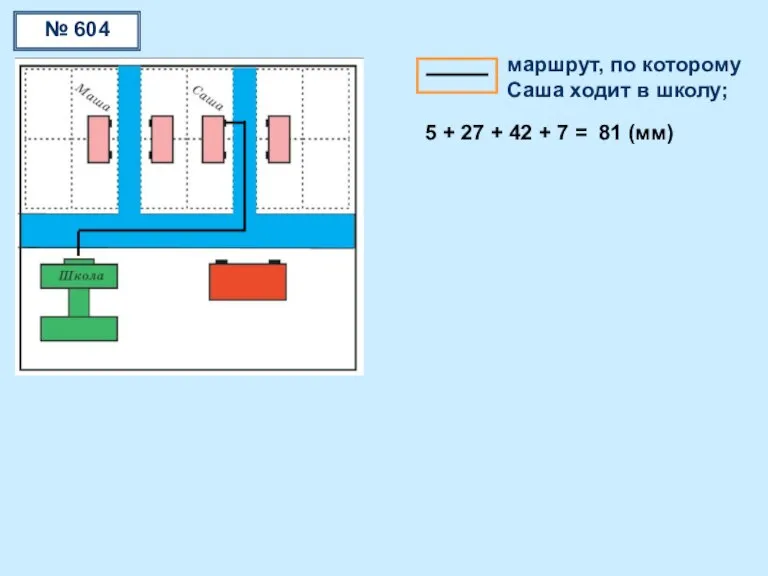 Задачи на расстояние
Задачи на расстояние Присчитывание и отсчитывание по 2
Присчитывание и отсчитывание по 2 Первое появление понятия многогранников
Первое появление понятия многогранников Письмове додавання трицифровий чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам. Урок 82
Письмове додавання трицифровий чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам. Урок 82 Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4)
Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4) Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Выполни тест в электронном дневнике. Устный счёт
Выполни тест в электронном дневнике. Устный счёт Графы. Пути с таблицами
Графы. Пути с таблицами Метрологические основы анализа
Метрологические основы анализа Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Тригонометрия в биологии и медицине
Тригонометрия в биологии и медицине Тригонометрический круг
Тригонометрический круг Пифагоровы тройки чисел
Пифагоровы тройки чисел Презентация на тему Деление двузначного числа на однозначное
Презентация на тему Деление двузначного числа на однозначное  Степень с целым показателем. Блиц-опрос
Степень с целым показателем. Блиц-опрос Диаграммы
Диаграммы Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Повторение изученного материала, 1 класс
Повторение изученного материала, 1 класс Многонранники в нашей жизни
Многонранники в нашей жизни Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Многоугольники в нашей жизни
Многоугольники в нашей жизни Формулы приведения. Математический диктант
Формулы приведения. Математический диктант Направления и лучи
Направления и лучи Современная финансовая математика
Современная финансовая математика Метод комплексных амплитуд при моделировании радиосистем. Лекция 12
Метод комплексных амплитуд при моделировании радиосистем. Лекция 12 Оригами. Проект по математике
Оригами. Проект по математике Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью