Описательная статистика

Робастные показатели
Робастный означает устойчивый (не зависящий от предположения о типе распределения, от наличия вылетающих наблюдений)
Простейшие робастные показатели центральной тенденции
Усеченное среднее
Винзоризированное среднее
Медиана
Пример:
> x<-c(8,8,8,8,8,8,8,8)
> central(x)
Медиана 8
Арифметическое среднее 8
Геометрическое среднее 8
Гармоническое среднее 8
> mean(x,trim=0.2)
[1] 8
> x<-c(8,8,8,8,8,8,8,80)
> central(x)
Медиана 8
Арифметическое среднее 17
Геометрическое среднее 10.66817
Гармоническое среднее 9.014085
> mean(x,trim=0.2)
[1] 8

Робастные показатели
В теории оценок принято анализировать чувствительность показателя центральной тенденции к вылетающим наблюдениям по проценту таких наблюдений, который необходим, чтобы "сместить" показатель центральной тенденции (оценка станет нестабильной - небольшие изменения не в счет).
Показатель носит название "точки разрушения" (breakpoint/ breakdown point), но лучше называть его показателем устойчивости.
Вторым важнейшим показателем является эффективность, под которой понимают наименьшую дисперсию данных вокруг показателя (поскольку дисперсия - это показатель "близости" данных к показателю, то чем она меньше, тем лучше, точнее, суммарное описание данных, предлагаемое этим показателем).
У арифметического среднего точка разрушения (устойчивость) нулевая (первое же вылетающее значение непредсказуемо меняет его), зато высокая эффективность.
У медианы точка разрушения 50%, зато эффективность невысока.

Робастные показатели
Лучше иметь возможность отсекать наблюдения не симметрично (потеря данных) – М-оценки
Одношаговый метод: определить количество вылетающих наблюдений по обе стороны от медианы - рассчитать разности всех значений с медианой и поделить их на медиану абсолютных различий
MAD, взятую с поправочным коэффициентом для уравнивания со стандартным отклонением (надо умножить на 1,4826)
Предположим , что есть следующий набор из 19 наблюдений:
77 81 88 114 151 210 219 246 253 262 296 299 306 376 428 515 666 1310 2611.
Медиана равна 262, а MAD - 169. Для каждого значения рассчитываем разность с медианой, отнесенную к MAD и получаем следующий набор значений:
-1,09 -1,04 -1,035 -0,88 -0,66 -0,31 -0,25 -0,095 -0,05 0,00 0,20 0,22 0,26 0,67 0,98 1,50 2,39 6,2 13,90.
Далее необходимо найти вылетающие значения, которые по модулю превышают 1,28.
отрицательных значений -нет
положительные - четыре наибольших значения.
Теперь надо подсчитать сумму всех значений, которые не являются вылетающими.
Сумма равна 3406.
М-оценка центральной тенденции определяется как произведение константы К (равной 1,28) на MAD и на разность количества вылетающих наблюдений (положительные минус отрицательные) в сумме со значениями, не являющимися вылетающими и все это делится на количество не вылетающих наблюдений.
М-оценка центральной тенденции равна (формула):
М=[K*MAD*(n+-n-)+S]/(N-n+-n-),
где n+ - количество вылетающий наблюдений справа (наибольшие вылетающие наблюдения); n- - количество вылетающих наблюдений слева (наименьшие вылетающие наблюдения); S – сумма не вылетающих наблюдений и N – общее количество наблюдений.
В анализируемом примере числитель будет равен 1,28*169*(4-0)+3406=4271,28, а знаменатель - (19-4)=15.
М-оценка составит 4271,28/15=285.

Робастные показатели
М-оценка (R)
library(MASS)
xs<-c(77, 81, 88, 114, 151, 210, 219, 246, 253, 262, 296, 299, 306, 376, 428, 515, 666, 1310, 2611)
huber(xs, k=1.28)
$mu
[1] 284.7575
$s
[1] 169.0164

Робастные показатели
МОМ (малые группы)
Аналогичен обычным М-оценкам, но не включает в числителе произведения, содержащего MAD и использует К равное 2,24
В разобранном выше примере при оценке МОМ вылетающими будут признаны только 3 наибольших значения.
Сумма не вылетающих значений (числитель) будет равна 3406+515=3921.
Количество не вылетающих наблюдений равно 16
МОМ равна 3921/16=245,1

Робастные оценки
data xs;
input xs @@;
gr=1;
cards;
77 81 88 114 151 210 219 246 253 262 296 299 306 376 428 515 666 1310 2611
;
run;
proc robustreg method=M(wf=talworth(c=2.24));
class gr;
model xs=gr;
run;

Как описывать показатели центральной тенденции
Количественные переменные:
Симметричное распределение данных - среднее арифметическое
Скошенное распределение данных (длинный "хвост" в одну сторону) - среднее геометрическое
Распределение с длинными "хвостами" - среднее гармоническое
Неизвестное распределение, с необычными (скошенными, тяжелыми) «хвостами» или наличием необычных (вылетающих) наблюдений - обрезанное или винзоризированное среднее, M-оценки, МОМ
Теоретически известное распределение, в котором средние плохо описывают центральную тенденцию – максимально правдоподобный параметр (MLE)
Полуколичественные переменные
Количество наблюдений примерно равно или меньше количества классов - медиана
Количество наблюдений значительно больше количества классов - мода
Качественные переменные
Данные получены на всех объектах одновременно - доля объектов каждого класса
Данные получены в результате разной продолжительности наблюдения за объектами (выживаемость)
Скорость наступления исходов предполагается постоянной - численность исходов в единицу времени
Скорость наступления исходов не может приниматься постоянной - эмпирическая функция выживаемости, медиана выживаемости

Методы описания показателей разброса данных

Простейшие
Разброс (амплитуда)
Дисперсия (стандартное отклонение)

Робастные
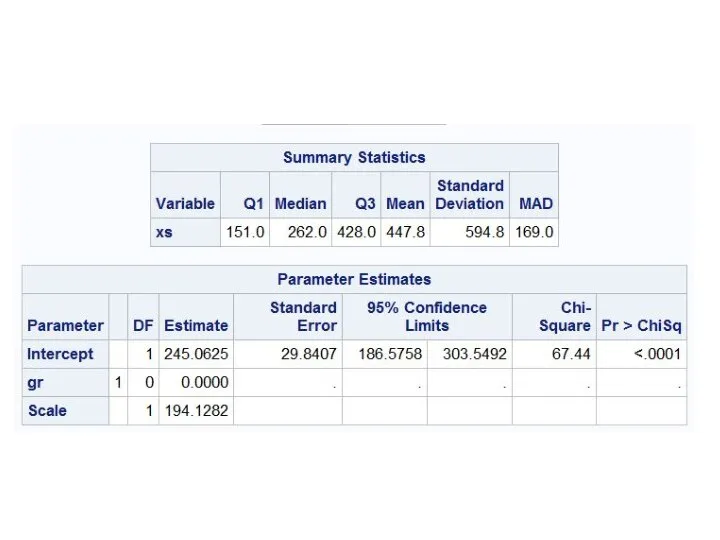
Стандартное отклонение для усеченных и винзоризированных средних
Для винзоризированных средних стандартное отклонение считается аналогичным образом, как и для арифметического среднего, а вот для обрезанного среднего используется винзоризированное, деленное на дополнение до единицы удвоенной доли «обрезания», т.е. для 20% отбрасывания значений знаменатель будет равен (1-2*0,2)=0,6.
Пример.
Пусть есть следующий набор данных, представленный суммарным баллом при заполнении анкеты:
7, 9, 10, 10, 13, 13, 13, 14, 17, 18
Среднее значение равно 12,4.
Дисперсия равна сумме квадратов разности каждого значения с 12,4, деленной на 9.
Сумма квадратов разности равна 108,4,
Дисперсия равна 12,04, а стандартное отклонение – 3,47.
Если использовать удаление 10% наблюдений, то обрезанное среднее все равно будет 12,4.
После винзоризации набор данных будет выглядеть так:
9, 9, 10, 10, 13, 13, 13, 14, 17, 17
Поэтому винзоризированное среднее будет равно 12,5, а стандартное отклонение – 2,99.
Стандартное отклонение обрезанного среднего оценивается путем деления винзоризированного на (1-2*0,1)=0,8 и будет равно 3,74.

Робастные
Межквартильное расстояние
MAD
Tn Rousseeuw и Croux, (1993)
Более эффективный, но мало где рассчитывается автоматом

Tn в SAS
data xs;
input xs @@;
gr=1;
id=_n_;
cards;
77 81 88 114 151 210 219 246 253 262 296 299 306 376 428 515 666 1310 2611
;
run;
PROC SQL;
CREATE TABLE _ntab AS
SELECT prim.xs, ABS(prim.xs - sec.xs) AS diff
FROM xs AS prim, xs AS sec
WHERE prim.id<>sec.id;
QUIT;
PROC MEANS NOPRINT NWAY;
CLASS xs;
VAR diff;
OUTPUT OUT=_n MEDIAN=MEDIAN;
RUN;
DATA _null_;
IF 0 THEN SET _n nobs=nobs;
CALL SYMPUTX("nobs",nobs);
STOP;
RUN;
DATA _n;
SET _n;
h=&nobs/2+1;
IF _n_
RUN;
PROC MEANS NWAY NOPRINT;
OUTPUT OUT=_Tn SUM(median)=MED MEAN(h)=h;
RUN;
DATA _Tn;
SET _Tn;
Tn=1.3800*MED/h;
RUN;
proc print; run;

Tn в R
library(RMySQL)
xs<-c(77, 81, 88, 114, 151, 210, 219, 246, 253, 262, 296, 299, 306, 376, 428, 515, 666, 1310, 2611)
id<-seq(1:length(xs))
new<-data.frame(id,xs)
con<-dbConnect(dbDriver("MySQL"),dbname="test")
dbWriteTable(con,"new",new)
xtab<-dbGetQuery(con,"
SELECT prim.xs, ABS(prim.xs - sec.xs) AS diff
FROM new AS prim,
new AS sec
WHERE prim.id<>sec.id;
")
dbRemoveTable(con,"new")
dbDisconnect(con)
foo<-tapply(xtab$diff,xtab$xs,median)
h<-length(foo)/2+1
Tn<-1.3800*sum(foo[seq(1:h)])/h
Tn

Tn

Как описывать разброс
Для количественных данных - стандартное отклонение (включая стандартное отклонение винзоризированных и обрезанных средних)
Для полуколичественных данных - межквартильное расстояние или MAD

Бивариантный анализ
Как описывать связи

Количественная зависимая
Количественная зависимая переменная и количественная независимая переменная
Коэффициент линейной регрессии в случае нормальности распределения остатков
Робастный коэффициент регрессии (Thiel) в случае наличия вылетающих наблюдений
Связь между двумя количественными переменными
Коэффициент корреляции Спирмена
Количественная зависимая переменная и ординальная независимая переменная
Коэффициент ранговой регрессии или робастный коэффициент регрессии
Связь между количественной и ординальной переменными
Коэффициент корреляции Спирмена или тау Кендала

Ординальная зависимая
Ординальная зависимая переменная и количественная или ординальная независимая переменная (большое количество классов независимой переменной)
Коэффициент ранговой регрессии или робастный коэффициент регрессии
Ординальная зависимая переменная и количественная или ординальная независимая переменная (малое количество классов независимой переменной)
Коэффициенты ординальной логистической регрессии
Связь между ординальными переменными
Коэффициент корреляции Спирмена, тау Кендала