Презентация на тему Движение

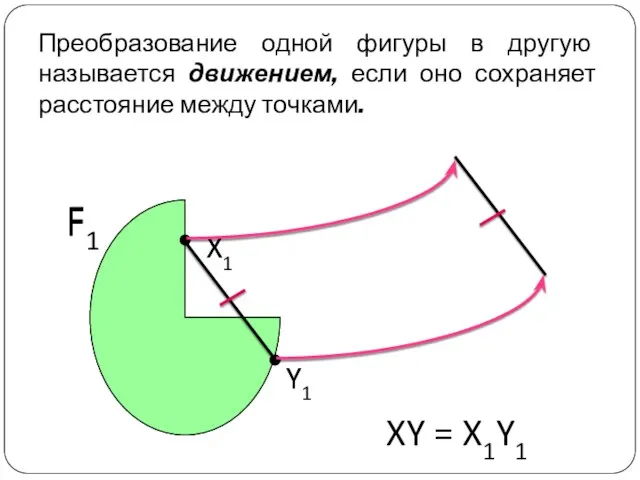
Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками.
Y1
XY = X1Y1

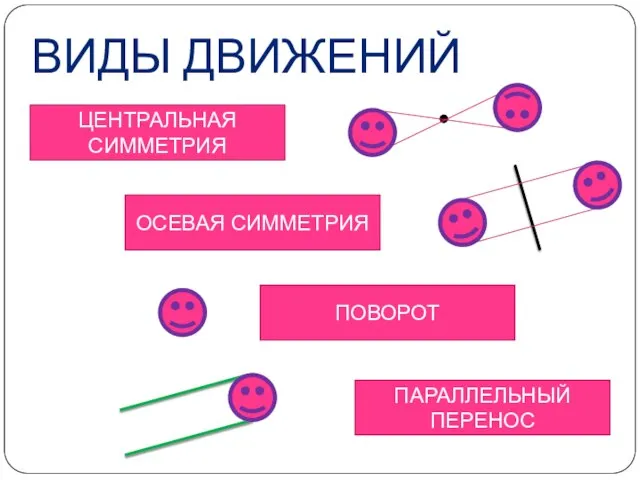
ВИДЫ ДВИЖЕНИЙ
ОСЕВАЯ СИММЕТРИЯ
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
ПОВОРОТ
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС

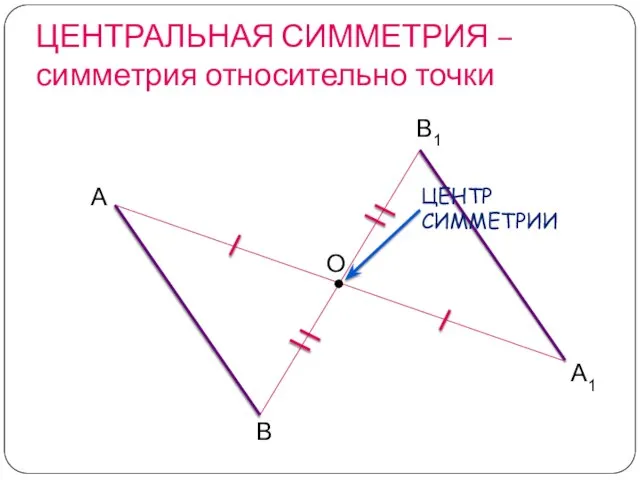
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки
А1
А
В
В1
О

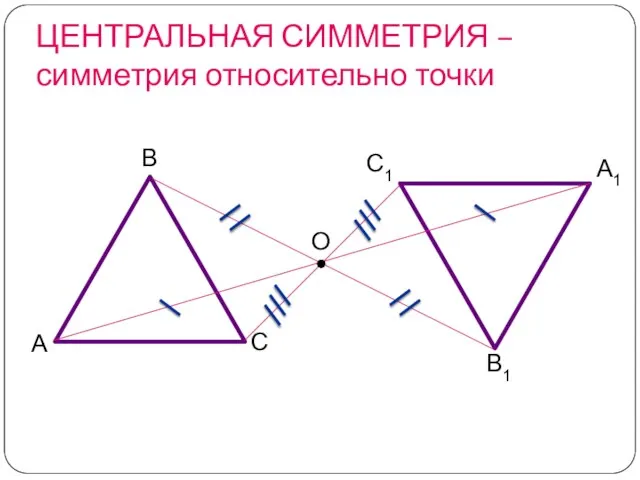
О
А1
В1
С1
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки

чтобы построить фигуру, симметричную данной относительно точки О, нужно каждую точку фигуры соединить с точкой О, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ – симметрия относительно точки
Сделаем вывод:
СВОЙСТВА ДВИЖЕНИЯ

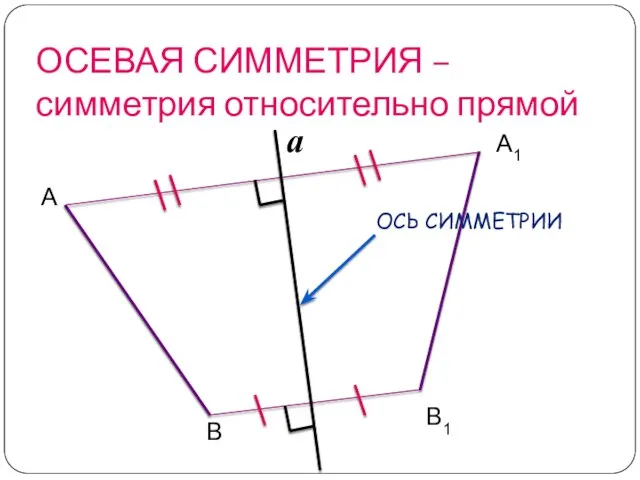
ОСЕВАЯ СИММЕТРИЯ –
симметрия относительно прямой
А
В
А1
В1
a

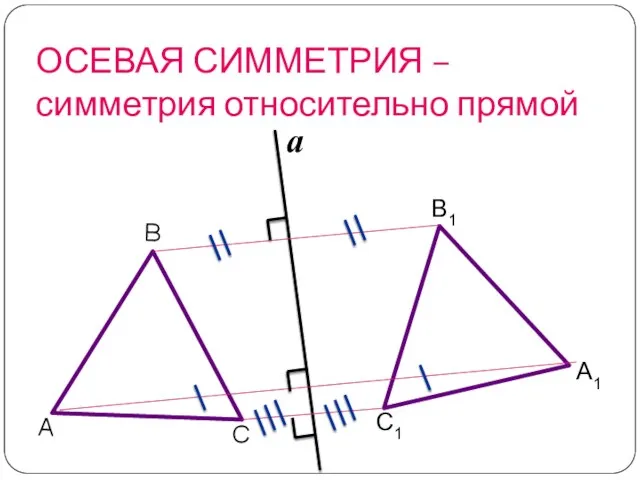
ОСЕВАЯ СИММЕТРИЯ –
симметрия относительно прямой
С1
А1
В1
a

чтобы построить фигуру, симметричную данной относительно прямой а, нужно из каждой точки фигуры провести перпендикуляр к прямой а, продолжить полученный отрезок равным ему, отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы
ОСЕВАЯ СИММЕТРИЯ –
симметрия относительно прямой
Сделаем вывод:
СВОЙСТВА ДВИЖЕНИЯ

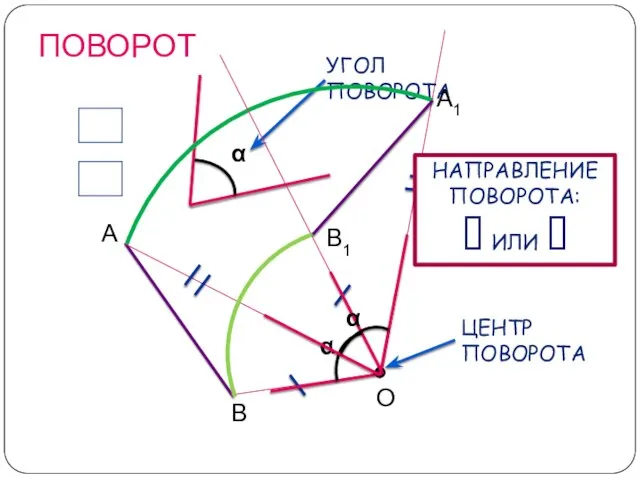
ПОВОРОТ
О
А
В
А1
В1
НАПРАВЛЕНИЕ ПОВОРОТА:
 ИЛИ 


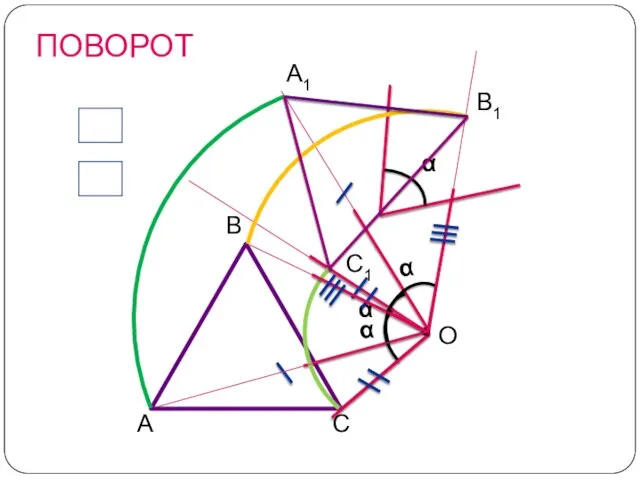
ПОВОРОТ
О
А1
В1
С1


ПОВОРОТ
Сделаем вывод:
Чтобы получить отображение фигуры при повороте около данной точки, нужно каждую точку фигуры повернуть на один и тот же угол в одном и том же направлении (по часовой стрелке или против часовой стрелки)
СВОЙСТВА ДВИЖЕНИЯ

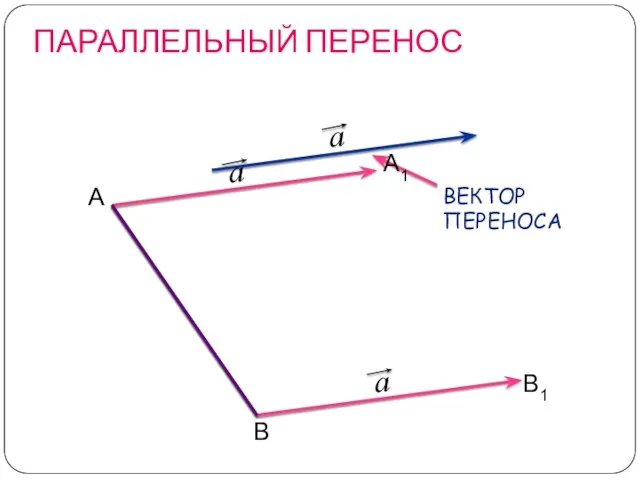
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
А
В
А1
В1

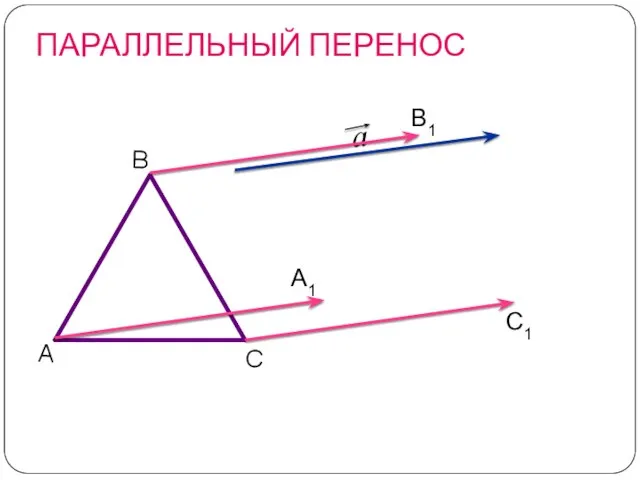
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
С1
А1
В1
С
А
В

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Сделаем вывод:
Чтобы отобразить фигуру с помощью параллельного переноса, нужно каждую точку фигуры переместить на заданный вектор, а затем соединить полученные образы
СВОЙСТВА ДВИЖЕНИЯ

СВОЙСТВА ДВИЖЕНИЯ
Попробуйте сформулировать
При движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки.
Точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Сохраняются углы между полупрямыми.
ЗНАЧИТ…

Любая фигура переходит
в равную ей фигуру

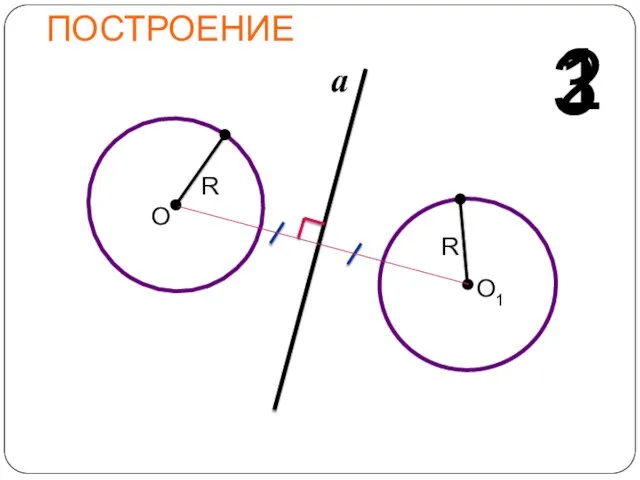
ЗАДАЧИ
1. Постройте окружность, симметричную данной относительно заданной прямой.
Решение:
для построения любой окружности нужно знать её центр и радиус.
Поэтому, для построения окружности, симметричной данной, нужно :
построить точку, симметричную центру;
измерить радиус исходной окружности;
этим же радиусом построить окружность с центром в симметричной точке.
ПОСТРОЕНИЕ

ПОСТРОЕНИЕ
О
a
1
О1
R
2
R
3

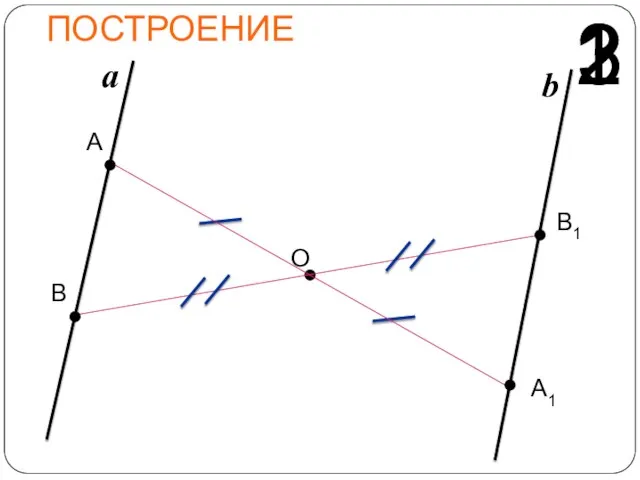
ЗАДАЧИ
2. Постройте прямую, симметричную данной относительно заданной точки.
Решение:
Мы знаем, что через две точки можно провести прямую и притом только одну.
Поэтому, для построения прямой, симметричной данной, нужно :
произвольно выбрать две точки на данной прямой;
построить симметричные им точки;
через полученные точки провести прямую – это и будет искомая прямая.
ПОСТРОЕНИЕ

ПОСТРОЕНИЕ
О
a
1
А
2
А1
3
В1
b
В

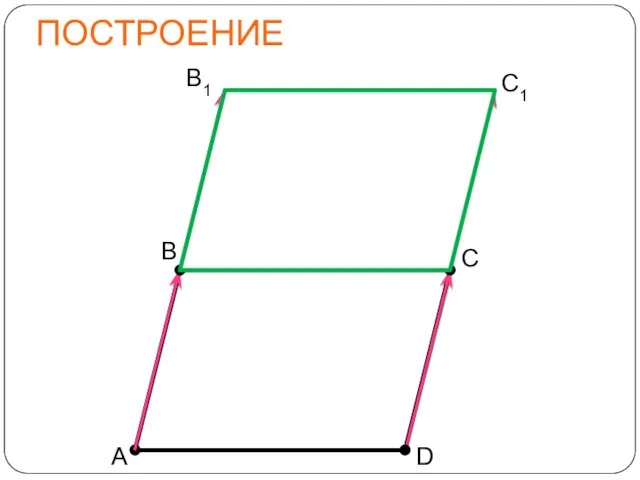
ЗАДАЧИ
3. Постройте параллелограмм, полученный с помощью параллельного переноса параллелограмма ABCD на вектор АВ.
Решение:
Вектор АВ пройдёт вдоль стороны АВ параллелограмма, значит
точка А перейдёт в точку В,
точка В переместится в этом же направлении на длину отрезка АВ в точку В1,
точка С перейдёт таким же образом в точку С1,
точка D перейдёт в точку С.
Таким образом, параллелограмм ABCD перейдёт в параллелограмм ВВ1С1С.
ПОСТРОЕНИЕ



ПОСТРОЕНИЕ
D
А
С
В1
В
С1

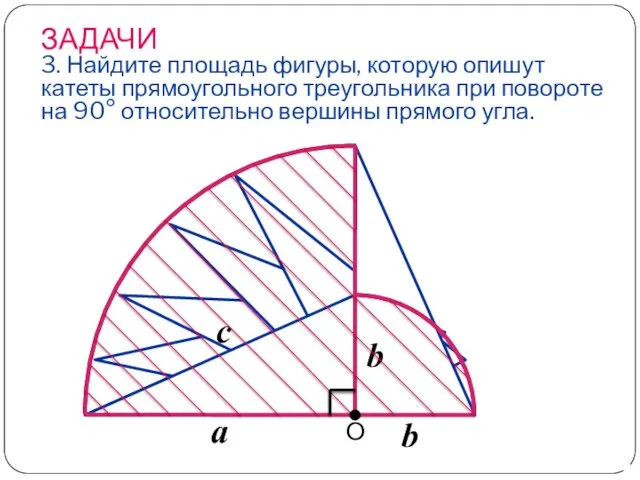
ЗАДАЧИ
3. Найдите площадь фигуры, которую опишут катеты прямоугольного треугольника при повороте на 90 относительно вершины прямого угла.
b
a
b
c
РЕШЕНИЕ
О

Решение:
При повороте каждый катет прямоугольного треугольника описал круговой сектор с дугой 90, а точнее – четверть круга.
Радиусом одного сектора является катет а,
радиусом второго сектора – катет b.
Следовательно, площади этих секторов будут вычисляться по формулам:
и
Соответственно, для всей фигуры:
или

ДОМАШНЕЕ ЗАДАНИЕ
Определите, при каких видах движения переходят сами в себя следующие фигуры:
квадрат,
прямоугольник,
ромб,
параллелограмм,
равнобокая трапеция,
равносторонний треугольник,
круг.
Для симметрии укажите центр или ось симметрии,
для поворота – центр, угол и направление поворота,
для параллельного переноса – вектор переноса.