Алгебра логики. Понятие алгебры логики

ПОНЯТИЕ АЛГЕБРЫ ЛОГИКИ
Алгебра логики является разделом развивающейся науки – дискретной математики.
Дискретная математика занимается изучением свойств структур конечного характера, которые возникают как внутри математики, так и в ее приложениях.

СТРУКТУРЫ ДИСКРЕТНОЙ МАТЕМАТИКИ
К числу структур, изучаемых дискретной математикой, могут быть отнесены конечные группы, конечные графы, математические модели преобразователей информации и конечных автоматов.
Конечная группа — алгебраическая группа, содержащая конечное число элементов (это число называется её порядком) Конечные группы широко используются как в математике, так и в других науках: топология) Конечные группы широко используются как в математике, так и в других науках: топология, криптография) Конечные группы широко используются как в математике, так и в других науках: топология, криптография, кристаллография) Конечные группы широко используются как в математике, так и в других науках: топология, криптография, кристаллография, атомная физика) Конечные группы широко используются как в математике, так и в других науках: топология, криптография, кристаллография, атомная физика, теория орнаментов) Конечные группы широко используются как в математике, так и в других науках: топология, криптография, кристаллография, атомная физика, теория орнаментов и др. Они тесно связаны с симметрией исследуемых объектов
граф — это совокупность непустого множества вершин и множества пар вершин.

КИБЕРНЕТИКА
Наибольшего развития дискретная математика достигла в связи с запросами практики, приведшими к появлению новой науки – кибернетики.
Кибернетика – наука об общих законах получения, хранения, передачи и преобразования информации в сложных системах.

Термин кибернетика ввел американский ученый Норберт Винер (1894 – 1964)

ИСТОРИЯ ТЕРМИНА
Широкое использование ЭВМ и базирующихся на них АСУ (автоматизированных систем управления) потребовало создания научных основ проектирования ЭВМ и АСУ. Полученные научные методы и результаты объединили в новую науку, получившую в США и Англии название computer science, во Франции – Informatics. В СССР, а затем и в России название кибернетика было вытеснено (поглощено) названием информатика.

ЛОГИКА В ИНФОРМАТИКЕ
Математический аппарат алгебры логики широко используется в информатике, в частности, в таких ее разделах, как проектирование ЭВМ, теория автоматов, теория алгоритмов, теория информации, целочисленное программирование.

ОТЕЦ АЛГЕБРЫ ЛОГИКИ
Джордж Буль (1815 – 1864)

Джордж Буль
Построил один из разделов формальной логики в виде некоторой «алгебры», аналогичной алгебре чисел, но не сводящейся к ней. Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.

ВЫСКАЗЫВАНИЯ
Объектами алгебры логики являются высказывания.
Величины, которые отражают истинность высказываний, называют логическими величинами.
Логическая величина может иметь только одно из двух значений, которые выражают парой слов или чисел: «да» – «нет», «истина» – «ложь», 1 - 0

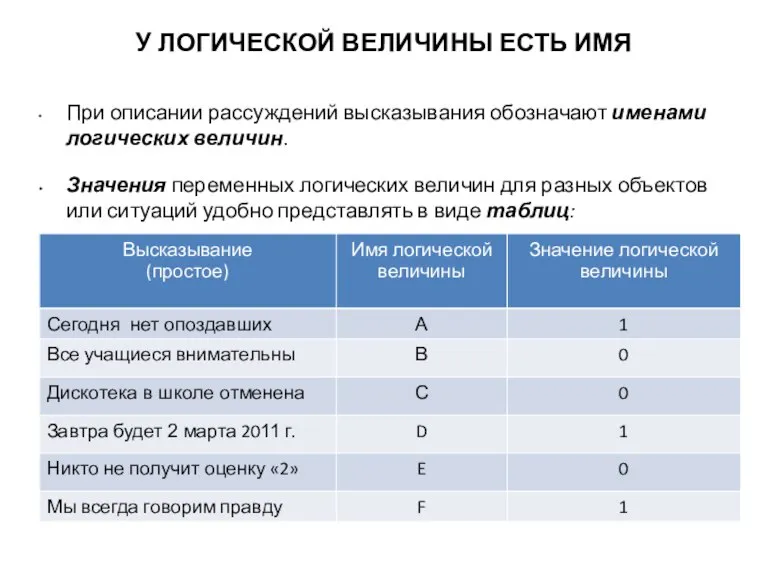
У ЛОГИЧЕСКОЙ ВЕЛИЧИНЫ ЕСТЬ ИМЯ
При описании рассуждений высказывания обозначают именами логических величин.
Значения переменных логических величин для разных объектов или ситуаций удобно представлять в виде таблиц:

ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Составные (сложные) высказывания образуются с помощью связок «И», «ИЛИ», «НЕ», которые в алгебре логики заменяются на логические операции:
Инверсия, логическое отрицание (НЕ);
Конъюнкция, логическое умножение (И);
Дизъюнкция, нестрогая дизъюнкция, логическое сложение (ИЛИ);
Разделительная (строгая) дизъюнкция, исключающее ИЛИ, сложение по модулю 2, неравнозначность (ЛИБО);
Импликация, следование (ЕСЛИ … , ТО);
Эквиваленция, эквивалентность,, разнозначность (ТОГДА И ТОЛЬКО ТОГДА, КОГДА).

ТАБЛИЦЫ ИСТИННОСТИ
Логические операции задаются таблицами истинности, в которых отображаются их значения.
Таблица истинности — это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.

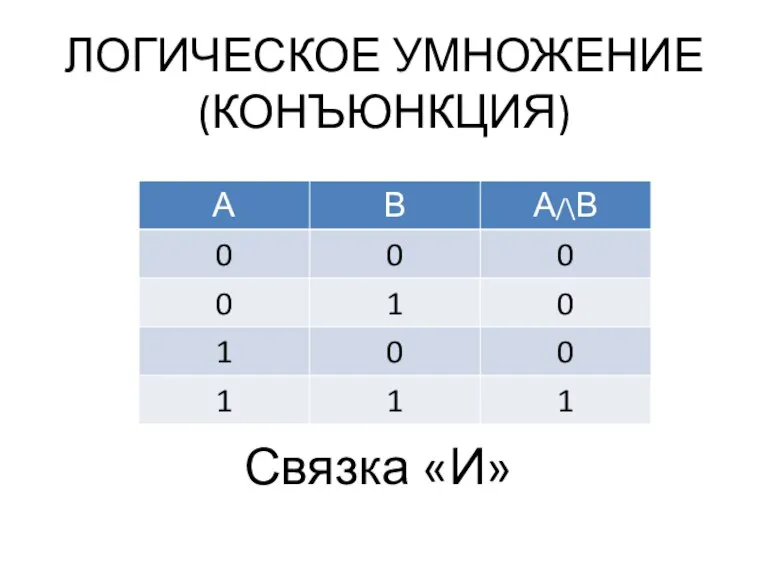
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ
(КОНЪЮНКЦИЯ)
Связка «И»

«истина» и «истина» = «истина»
«истина» и «ложь» = «ложь»
«ложь» и «истина» = «ложь»
«ложь» и «ложь» = «ложь»
ПРИМЕРЫ КОНЪЮНКЦИИ

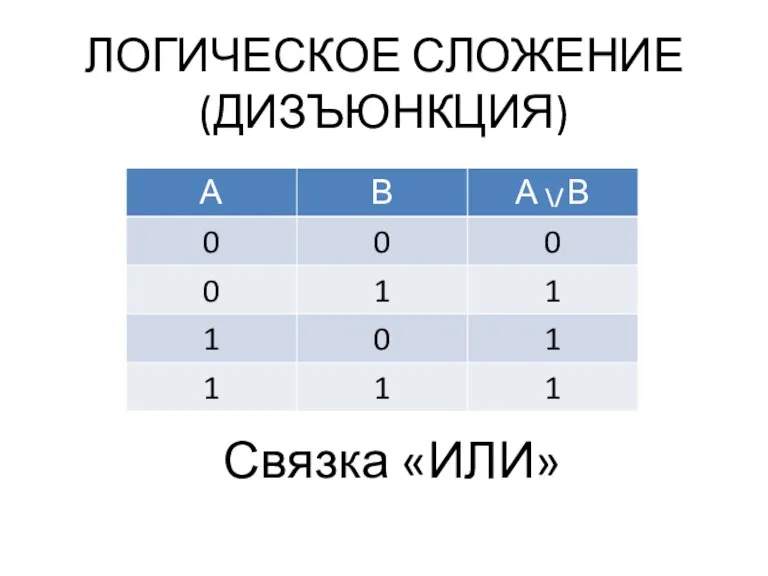
ЛОГИЧЕСКОЕ СЛОЖЕНИЕ
(ДИЗЪЮНКЦИЯ)
Связка «ИЛИ»

«истина» или «истина» = «истина»
«истина» или «ложь» = «истина»
«ложь» или «истина» = «истина»
«ложь» или «ложь» = «ложь»
ПРИМЕРЫ ДИЗЪЮНКЦИИ

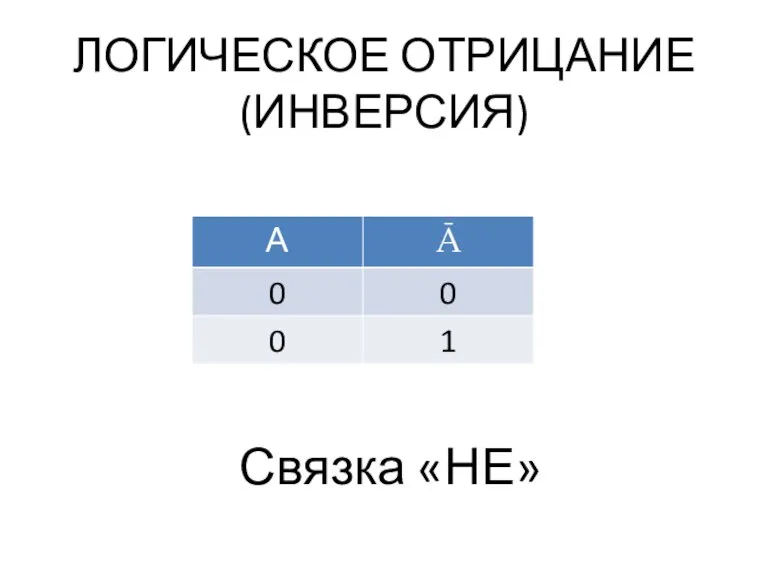
ЛОГИЧЕСКОЕ ОТРИЦАНИЕ
(ИНВЕРСИЯ)
Связка «НЕ»

не «истина» = «ложь»
не «ложь» = «истина»
ПРИМЕРЫ ИНВЕРСИИ

ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ
Составное высказывание, выраженное в виде формулы, называется логическим выражением.
В логическом выражении простые высказывания обозначают именами логических величин.
Величины, которые отражают истинность высказываний, называют логическими величинами.

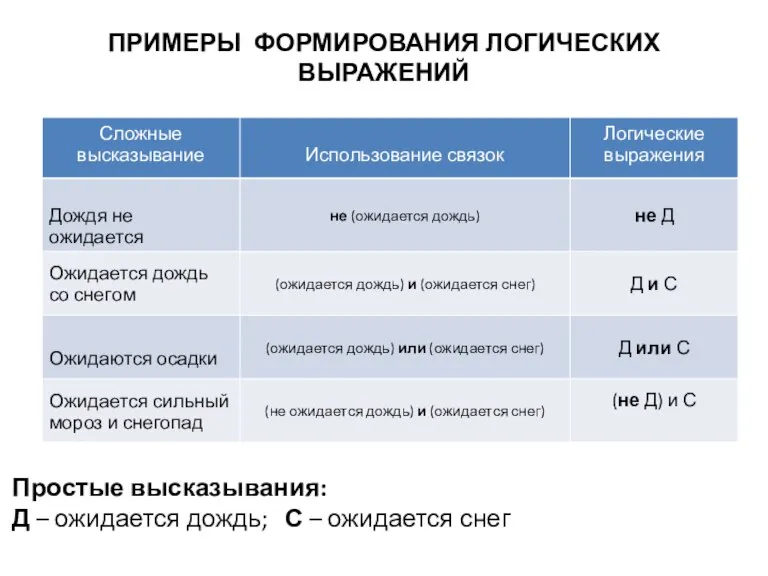
ПРИМЕРЫ ФОРМИРОВАНИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
Простые высказывания:
Д – ожидается дождь; С – ожидается снег

ПРАВИЛА ОПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
Выражение, составленное из одной логической величины и связки «не», имеет значение, противоположное значению величины.
Выражение, составленное из двух величин и связки «и», имеет значение «истина», только если значение «истина» имеют обе величины.
Выражение, составленное из двух величин и связки «или», имеет значение «истина», если значение «истина» имеет хотя бы одна величина. Такое выражение имеет значение «ложь», только если значения обеих величин – «ложь».

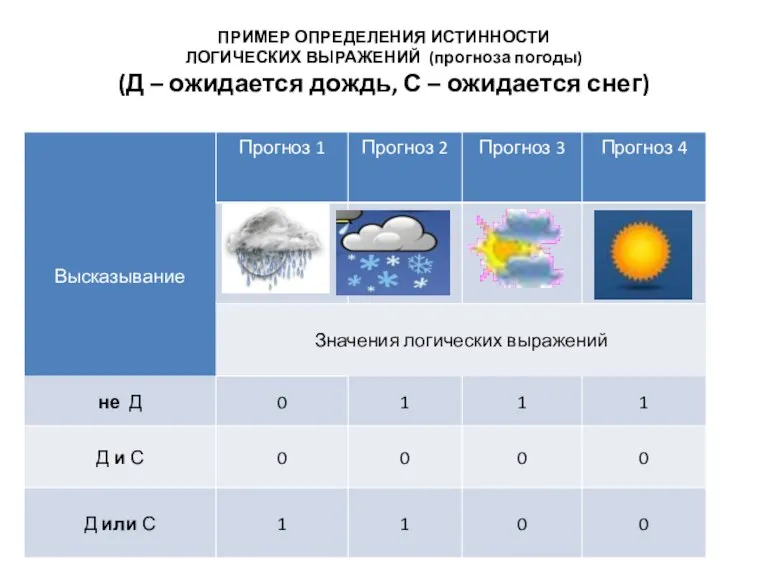
ПРИМЕР ОПРЕДЕЛЕНИЯ ИСТИННОСТИ
ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ (прогноза погоды)
(Д – ожидается дождь, С – ожидается снег)

САМОСТОЯТЕЛЬНАЯ РАБОТА
Заполнить значениями истинности логических выражений таблицу
(выдана в начале урока)
Время выполнения - 10 минут

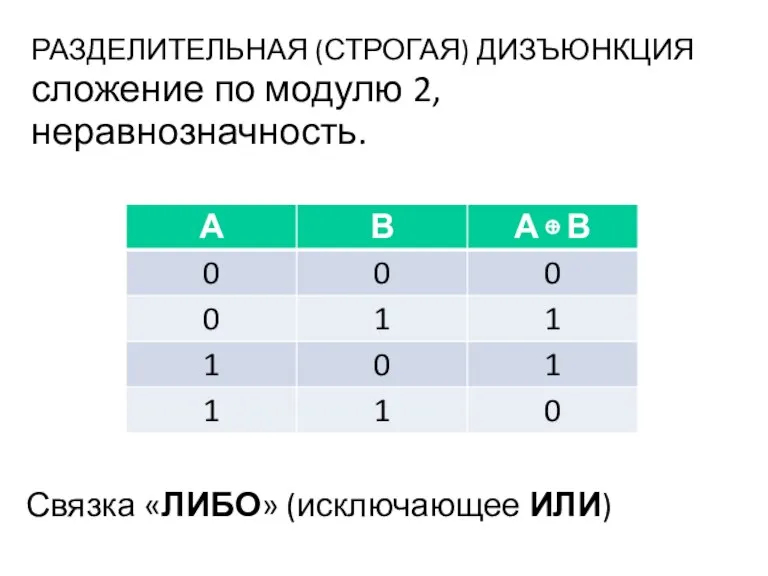
РАЗДЕЛИТЕЛЬНАЯ (СТРОГАЯ) ДИЗЪЮНКЦИЯ
сложение по модулю 2, неравнозначность.
Связка «ЛИБО» (исключающее ИЛИ)

В высказывании, являющемся разделительной дизъюнкцией, мы утверждаем, что произойдет только одно событие.
Она двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся истинным только тогда, когда только одно из высказываний является истинным.

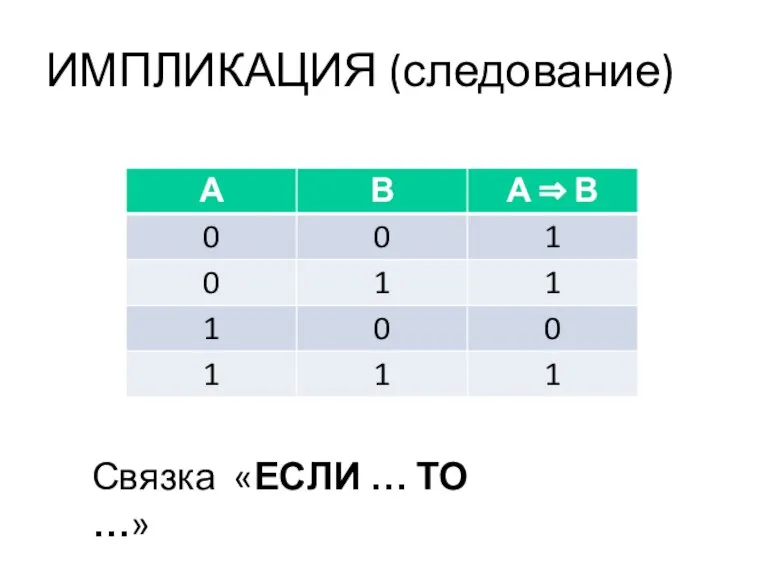
ИМПЛИКАЦИЯ (следование)
Связка «ЕСЛИ … ТО …»

Импликация – логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Импликация будет ложной только тогда, когда посылка истинна, а заключение ложно, и она заведомо будет истинна, если ее условие ложно.

Другими словами, из неверного условия может следовать все, что угодно. Например, высказывание: «если 2 > 3, то крокодилы летают» – является истинным.
Например, истинны следующие высказывания:
1) Если 2х2=4, то Монгохто находится в Европе;
2) Если Монгохто находится в Африке, то 2х2=4;
3) Если Монгохто находится в Африке, то 2х2=5;
4) Если не наступит Новый год, то чернила высохнут;
5) Если Монгохто находится в Африке, то Нового года не будет.
Те импликации, в которых посылки и заключения являются предложениями без взаимной связи, не играют в науке никакой роли. Это совершенно бесплодные предложения.
Большинство математических теорем являются импликациями.
Но если в теореме условие и заключение не связаны по содержанию, то такая теорема не является импликацией.

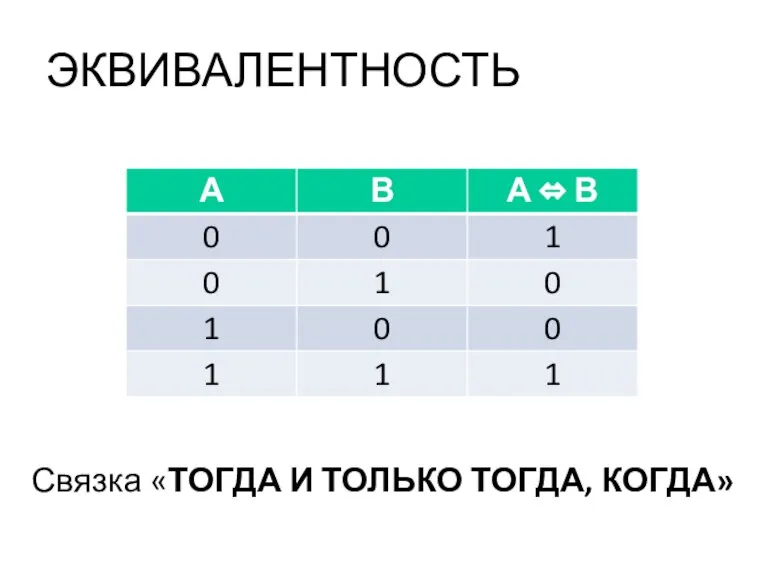
ЭКВИВАЛЕНТНОСТЬ
Связка «ТОГДА И ТОЛЬКО ТОГДА, КОГДА»

Эквивалентность – логическая операция, ставящая в соответствие двум элементарным высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Эквивалентность используется при необходимости выразить взаимную обусловленность.
Пример: «Я получу паспорт тогда и только тогда, когда мне исполнится 14 лет».