Содержание
- 2. Иррациональным уравнением называется уравнение, содержащее неизвестную под знаком радикала, а также под знаком возведения в дробную
- 3. Основные методы решения иррациональных уравнений: возведение в степень обеих частей уравнения; введение новой переменной; разложение на
- 4. Дополнительные методы решения иррациональных уравнений: умножение на сопряженное; переход к уравнению с модулем; метод «пристального взгляда»
- 6. Метод возведения в степень обеих частей уравнения: 1) Если иррациональное уравнение содержит только один радикал, то
- 7. Метод возведения в степень обеих частей уравнения: 2) Если в иррациональном уравнении содержится два или более
- 14. Метод введения новой переменной Данный метод применяется в том случае, когда в уравнении неоднократно встречается некоторое
- 19. Метод разложения на множители Для решения иррациональных уравнений данным методом следует пользоваться правилом: Произведение равно нулю
- 23. Дополнительные методы решения иррациональных уравнений: метод «пристального взгляда» (метод анализа уравнения); использование монотонности функции; переход к
- 24. Метод анализа уравнения Свойства корней, которые используют при решении уравнений данным способом: 1. Все корни четной
- 27. Метод использования монотонности функции Сформулируем два свойства монотонных функций: 1. Сумма возрастающих (убывающих) функций – функция
- 28. Метод использования монотонности функций Теорема о корне Пусть y=f(x) – монотонная на некотором промежутке функция. Тогда
- 30. Метод перехода к уравнению с модулем
- 35. Скачать презентацию



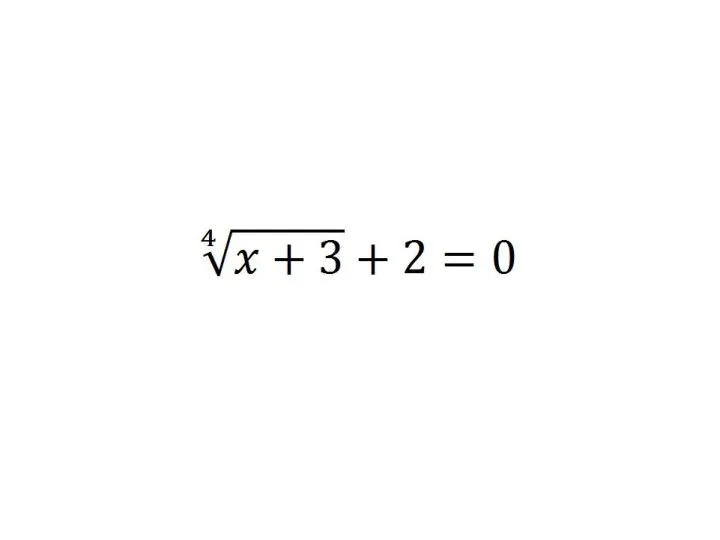




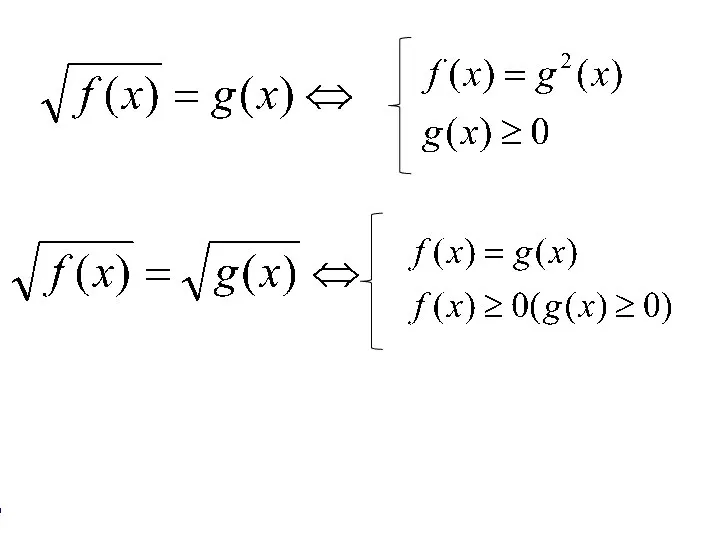























 Дифференциальные уравнения. Основные понятия
Дифференциальные уравнения. Основные понятия Знаки математических действий
Знаки математических действий be798f8c4ede43fcabd1090e739d523d
be798f8c4ede43fcabd1090e739d523d Средняя линия треугольника
Средняя линия треугольника Логарифм числа
Логарифм числа Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Презентация на тему Осевая симметрия
Презентация на тему Осевая симметрия  Информатика. Вероятность
Информатика. Вероятность Вавилонская математика
Вавилонская математика Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Трапеция
Трапеция Урок по математике
Урок по математике Равнобедренный треугольник
Равнобедренный треугольник Среднеквадратическое отклонение
Среднеквадратическое отклонение Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Эти годы позабыть нельзя. Интегрированный урок
Эти годы позабыть нельзя. Интегрированный урок Величины. Масса (1 класс)
Величины. Масса (1 класс) Прибавить и вычесть число 3. Решение текстовых задач
Прибавить и вычесть число 3. Решение текстовых задач Работа на повторение материала 6 класса
Работа на повторение материала 6 класса Подобие фигур вокруг нас
Подобие фигур вокруг нас Задачі_на_наслідки_із_аксіом_стереометрії
Задачі_на_наслідки_із_аксіом_стереометрії Построения графиков тригонометрических функций
Построения графиков тригонометрических функций Презентация на тему Логарифмы
Презентация на тему Логарифмы  Параллельные прямые в пространстве
Параллельные прямые в пространстве ОГЭ. Приемы решения практико-ориентированных задач
ОГЭ. Приемы решения практико-ориентированных задач Треугольники. Треугольник в науке
Треугольники. Треугольник в науке Оптические иллюзии
Оптические иллюзии Число 0. Цифра 0. Дистанционный урок
Число 0. Цифра 0. Дистанционный урок