Содержание
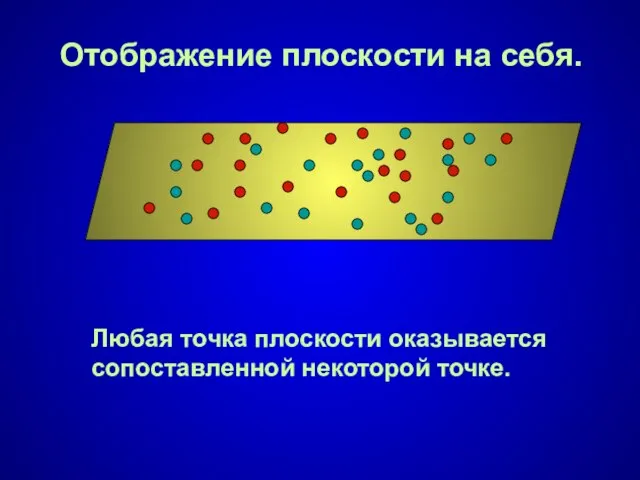
- 2. Отображение плоскости на себя. Любая точка плоскости оказывается сопоставленной некоторой точке.
- 3. Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
- 4. Понятие движения в геометрии связано с обычным представлением о перемещении. Но, если говоря о перемещении, мы
- 5. Два движения, выполненные последовательно, снова дают движение.
- 6. Параллельный перенос Осевая симметрия Поворот вокруг точки Центральная симметрия. На плоскости существует четыре типа движений:
- 7. Параллельным переносом называется такое движение , при котором все точки плоскости перемещаются в одном и том
- 8. Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения: Осевая симметрия
- 9. 1) Отражательная симметрия. В математике осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных
- 10. 2) Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию относительно поворотов вокруг прямой.
- 11. С симметрией мы часто встречаемся в быту, архитектуре, технике, природе.
- 12. Поворотом является движение, т.е. отображением плоскости на себя, сохраняющим расстояниям. Поворот вокруг точки м N a
- 13. Центральной симметрий относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что
- 15. Скачать презентацию











 Математический хоккей
Математический хоккей Тригонометрия. Комплексные числа
Тригонометрия. Комплексные числа Умножение и деление рациональных чисел (тренажер)
Умножение и деление рациональных чисел (тренажер) Линейная функция
Линейная функция График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Примеры на 5
Примеры на 5 Определитель матрицы. Правило Крамера
Определитель матрицы. Правило Крамера Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Какой функции соответствует график
Какой функции соответствует график Вентцель Е.С. Теория вероятностей
Вентцель Е.С. Теория вероятностей Задания по математике (5 класс, часть 6)
Задания по математике (5 класс, часть 6) Задачи на уменьшение числа в несколько раз
Задачи на уменьшение числа в несколько раз Свойства логарифмов
Свойства логарифмов Симметрия и асимметрия
Симметрия и асимметрия Уравнение окружности и прямой
Уравнение окружности и прямой Презентация на тему Распределительный закон умножения
Презентация на тему Распределительный закон умножения  Проекции вектора на оси координат
Проекции вектора на оси координат По следам теоремы Пифагора
По следам теоремы Пифагора Устный счёт Прицепи вагоны. 2 класс
Устный счёт Прицепи вагоны. 2 класс Презентация на тему Длина отрезка
Презентация на тему Длина отрезка  Модуль числа. 6 класс
Модуль числа. 6 класс Компетентностный подход в развитии творческих способностей учащихся на уроках математики
Компетентностный подход в развитии творческих способностей учащихся на уроках математики Симметрия в технике
Симметрия в технике Решение треугольников
Решение треугольников Dei_774_stvitelnye_chisla
Dei_774_stvitelnye_chisla Правильные многоугольники
Правильные многоугольники Прямоугольник. Решение задачи 7
Прямоугольник. Решение задачи 7 Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл