Формула суммы n первых членов геометрической прогрессии

Математические знания могут применяться умело с пользой лишь в том случае, если они усвоены творчески.
А.Н. Колмогоров
Дорогой друг!
Сегодня у тебя необычный урок математики. Сегодня ты еще раз убедишься в том, что математика не только интересна сама по себе, но она необычайно полезна. В ходе сегодняшнего урока тебя ожидает большая радость творчества и огромное поле приложения математических знаний и умений.
Желаю тебе успехов и творческих радостей на уроке!

Ход урока
Организационный момент.
Проверка домашнего задания (5 мин. выборочно).
Устная работа (5 мин.).
Проверочный тест (5 мин.).
Историческая справка (5 мин.).
Изучение новой темы (10 мин.).
Исторические задачи (5 мин.).
Задачи на закрепление новой темы (5 мин.).
Домашнее задание (2 мин.).
Рефлексия (2 мин.).
Выставление оценок (5 мин.).

Устно
1. Сравните числовые последовательности
1). 1, 2, 4,; -8 …
2). 1; -2; 4; -8 …
3). 1; -2; -4; -8 …
4). 1, 2, 4, 8 …
Найдите закономерности. .
Какие из приведенных последовательностей являются геометрической прогрессией?
2. Сравните числовые последовательности
1). 2.,3; 3,5; 4,7; 5,9 …
2). -8; 1; -2; 4 …
3). 3; -9; 27; 81 …
4). 3; 5; 7; 9 …
Есть ли здесь арифметическая прогрессия?
Есть ли среди них геометрическая прогрессия?
3. Является ли число 1/4геометрической прогрессией 8; 4; 2 ..? Если да, то укажите номер.
.

Ответы теста
I – вариант
1. Числовая последовательность b1, b2, b3… bn… называется геометрической прогрессией,
если для всех натуральных чисел n выполняется равенство:
bn-1 = b1*q где b1= 0, q≠0
2. Формула n-го числа геометрической прогрессии b вычисляется b n = b1 *qⁿ-_1
3. Является ли геометрической прогрессией последовательность и почему?
5, 25, 125…
Назовите следующий член прогрессии.
Да , 625
4. b1 = 16, q = 1/2. Найти b2, b3, b4 геометрической прогрессии.
b1 = 16, b2= 16*1/2 = 8, b3= b2 *1/2 = 8=4, b4 = 4 *1/2= 2
5. bn - геометрической прогрессии b6=1/27 , q = 1/3. Найти b1
bn= b1 qn-1, b1 = bn /qn-1, b1= 1/27*(1/3)5= 1/27*3= 32 =9
II – вариант
1. Знаменателем геометрической прогрессии bn называется число qкоторое вычисляется по формуле:
q =b2 / b1 = bn-1 / bn
2. Если все члены геометрической прогрессии положительны, то каждый ее член, начиная со второго равен среднему геометрическому двух соседних с ним членов.
3. Является ли геометрической прогрессией последовательность: 36, 18, 9 … и почему? Назовите следующий член последовательности.
Да. 4,5
4. bn геометрической прогрессии, где b1 = 1, q = 2
Найти: b2 , b3 , b4 .
b2 = 1 * 2= 2 ; b3 = 2 * 2= 4 ; b4 = 4 * 2= 8
5. Найдите b1 геометрической прогрессии bn, если
b5 =1/64 ; q = 1/2
b1 = b5 /q4 ; b1 =1/64:(1/2)4 = 1/ 26 * 24 = 1/4

НАЗАД, В ИСТОРИЮ!
На связь между прогрессиями первым обратил внимание великий АРХИМЕД (ок. 287–212 гг. до н.э)
Термин “прогрессия” был введен римским автором Боэцием (в 6 веке) и понимался в более широком смысле, как бесконечная числовая последовательность. Названия “арифметическая” и “геометрическая” были перенесены из теории непрерывных пропорций, которыми занимались древние греки.
Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке). Формула суммы членов геометрической прогрессии дана в книге Евклида “Начала” (3 век до н.э.).
Правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книги абака» в 1202г. (Леонардо Пизанский)
Понятие числовой последовательности возникло и развивалось задолго до создания учения о функциях.

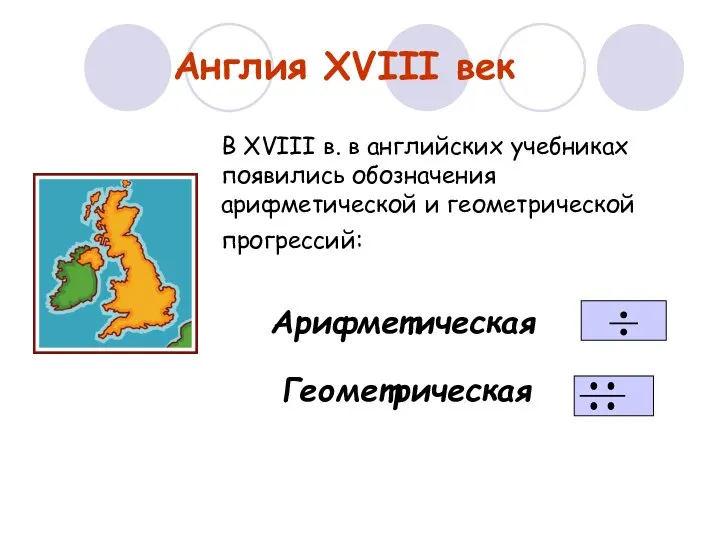
Англия XVIII век
В XVIII в. в английских учебниках появились обозначения арифметической и геометрической прогрессий:

Сведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции. Уже в V в. до н. э. греки знали следующие прогрессии и их суммы:
Древняя Греция

Древний Египет

Германия
Нашел моментально сумму всех натуральных чисел от 1 до 100, будучи еще учеником начальной школы.
1 + 2 + 3 + 4 + ….. + 99 + 100 = (1 + 100) + (2 + 99) + …… + (50 + 51) = 101 ∙ 50 = 5050
Решение
КАРЛ ГАУСС
(1777 – 1855)

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.

-Я достаточно богат, чтобы исполнить самое смелое твое пожелание, - продолжал царь. - Назови награду, которая тебя удовлетворит, и ты получишь ее.
Сета молчал.
-Не робей, - ободрил его царь. – Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его.
-Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра я сообщу тебе мою просьбу.
-Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, -сказал царь.
Мудрец поклонился.

Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.
-Повелитель, - сказал Сета, - прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
-Простое пшеничное зерно? – изумился царь.
-Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью - 4, за четвертую - 8, за пятую - 16, за шестую -32…

-Довольно, - с раздражением прервал его царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.
Сета улыбнулся хитро, покинул дворец и стал дожидаться у ворот дворца.

Почему так хитро улыбнулся Сета?
Прав ли был индусский царь, считая просьбу Сеты ничтожной, полагая, что все зерна пшеницы уместятся в один мешок?
Об этом ты узнаешь чуточку позже.

Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии.
Воспользуемся тем же приемом, с помощью которого была вычислена сумма в задаче№1. Пусть дана геометрическая прогрессия (bn). Обозначим сумму n первых ее членов через Sn:
Sn = b1 + b2 + b3 +………+bn-1 + bn. (1)
Умножим обе части этого равенства на q: Sn ·q = b1· q + b2 ·q + d3· q +…..+bn· q
Учитывая, что b1· q = b2, b2· q = b3,……bn-1· q = bn,
получим: Sn·q = b2 + b3 + b4+ ……+bn + dn· q (2)
Вычтем почленно из (2) равенство (1) и приведем подобные члены : Sn·q – Sn = (b2+b3+b4+….+bn+bn·q) – (b1+b2+b3+…..+bn) = bn·q – b1 ⇒ Sn(q – 1) = bn·q – b1
Sn = (bn·q – b1) / (q – 1)

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли Сета свою жалкую награду.
-Повелитель, - был ответ, - приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
-Повелитель, - ответили ему, - математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение.
Царь приказал ввести его.
-Прежде чем скажешь о твоем деле, - объявил Шерам, - я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
-Ради этого я и осмелился явиться перед тобой в столь ранний час, - ответил старик. – Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…..

-Как бы велико оно ни было, - надменно перебил царь, - житницы мои не оскудеют. Награда обещана и должна быть выдана..
- Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, которое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни.

С изумлением внимал царь словам старца.
- Назови мне это чудовищное число,- сказал он в раздумьи.
Пусть все пространство их будет сплошь засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду…

-Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три миллиарда семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!
18 446 744 073 709 551 615

Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, - но что награда, о которой говорит предание, должна была выразиться именно таким числом в этом ты сам можешь убедиться.
Фактически, число зерен, о которых идет речь, является суммой 64 членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:
S = 1+2+22+23+24+…….+262+263

S = 264 – 1
Значит, подсчет зерен сводится к перемножению 64 двоек. Для облегчения выкладок заменим 264 = (210)6 · 24 =
=1024 · 1024 ·1024· 1024 ·1024· 1024· 16 =
=1048576 ·1048576 ·1048576 ·16 – 1
и получим искомое число зерен:
18 446 744 073 709 551 615
Масса такого числа зерен больше триллиона тонн.
Индусский царь не в состоянии был выдать подобной награды.
Но будь он силен в математике, он бы не попал впросак…

Вывод
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая моря, и океаны, и горы, и пустыню, и Арктику с Антарктикой, и получить удовлетворительный урожай, то, пожалуй, лет за 5 он смог бы рассчитаться.
Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до настоящего времени.

Самостоятельная работа
Каждое задание имеет определенный «вес» в баллах. Постарайтесь набрать наибольшее количество баллов.
Дополнительное задание – на дополнительную оценку
Задания на карточках

Самостоятельная работа
1 вариант
1. Найти сумму семи первых членов геометрической прогрессии -2; -4; -8;… (3 балла)
2. Укажите сумму шести первых членов геометрической прогрессии, у которой b1=81, q=1/3. (3 балла)
3. Геометрическая прогрессия задана формулой n-го члена bn=5n-1. Найти S5. (4 балла)
4. Дополнительная задача. Рост дрожжевых клеток происходит делением каждой клетки на две части. Сколько дрожжевых клеток стало после пятикратного деления, если первоначально их было 1 млн. ?
Критерии оценки: 3–5 баллов — “3”, 6–8 баллов — “4”, 9 и более — “5”.
2 вариант
1. Найти сумму семи первых членов геометрической прогрессии, у которой b1=32, q=-2. (3 балла)
2. Укажите сумму пяти первых членов геометрической прогрессии 2;1; Ѕ ;… (3 балла)
3. Геометрическая прогрессия задана формулой n-го члена bn=3n. Вычислить S5. (4 балла)
4. Дополнительная задача. Каждое простейшее одноклеточное животное инфузория – туфелька размножается делением на 2 части. Сколько инфузорий стало после шестикратного деления, если первоначально их было 1000?

Сравни результаты
1 вариант
1) S7=- 254
2) S6=121
3) S5=781
4) 31 000 000 кл.
2 вариант
1) S7=1376
2) S5=3
3) S5=363
4) 63 000 инф.

Домашнее задание
а). п. 28 выучить формулы.
Задача 1
Некто продавал коня и попросил за него 1000 рублей. Купец сказал, что за коня запрошено слишком большая цена, «Хорошо, - ответил продавец, - возьми коня даром, а заплати только за гвозди в его подковах, А гвоздей во всякой подкове по 6 штук. За первый гвоздь - полушку ( 1 полушка – 1/2 копейки), за второй гвоздь - 2 полушки, за третий гвоздь -4 и т.д., за каждый гвоздь в 2 раза больше чем за предыдущий. Купец, думая, что заплатит на много меньше, чем 1000 рублей, согласился. Проторговался ли купец?
Задача 2
В нашем селе Филинском необходимо распространить информацию. Распространение происходит по следующей схеме. Каждый человек в течение часа должен проинформировать 4 человека. Первоначальной информацией владеют 2 человека. Всего не территории Филинского сельсовета проживают 2730 человек. Через какое время каждый житель Филинского будет информирован? Образует ли данная последовательность геометрическую прогрессию.
г). Придумать задачу на применение формулы суммы геометрической прогрессии.
Задачи на следующий урок:
Можно ли вывести формулу суммы n- первых членов геометрической прогрессии, зная b, bn, q, но не зная n? Как можно применить данные формулы для решения различных задач, связанных с геометрической прогрессией?

Ваше настроение

Спасибо!

Тест
Вариант 1
1. Дописать пропущенное: «Числовая последовательность b1, b2, b3, .... bn, .... Называется геометрической прогрессией, если для всех натуральных и выполняется равенство
. где b1 ≠ 0, g ≠ 0 »
2 Написать формулу n - члена геометрической прогрессии.
3. Является ли геометрической прогрессией последовательность; 5, 25, 125, и почему?
Назовите следующий член прогрессии.
4.(bn) - геометрическая прогрессия, b1 = 16, g = 1/2. Найдите b2, b3, b4.
5.(bn) - геометрическая прогрессия, b6 = 1/27, g = 1/3, Найдите b1.
Вариант 2
1. Дописать пропущенное: «Знаменателем геометрической прогрессии bп называется
число g, которое вычисляется по формуле....... . »
2. Дописать пропущенное: «Если все члены геометрической прогрессии положительны, то каждый ее член, начиная со второго равен ………….………..двух соседних с ним членов».
3. Является ли геометрической прогрессией последовательность: 36, 18, 9, и почему?
Назовите следующий член прогрессии.
4.(bn) - геометрическая прогрессия, b1 = 1, g = 2. Найдите b2, b3, b4
5.(bn) — геометрическая прогрессия. b5=1/64, g = 1/2: Найдите b1