Цилиндр

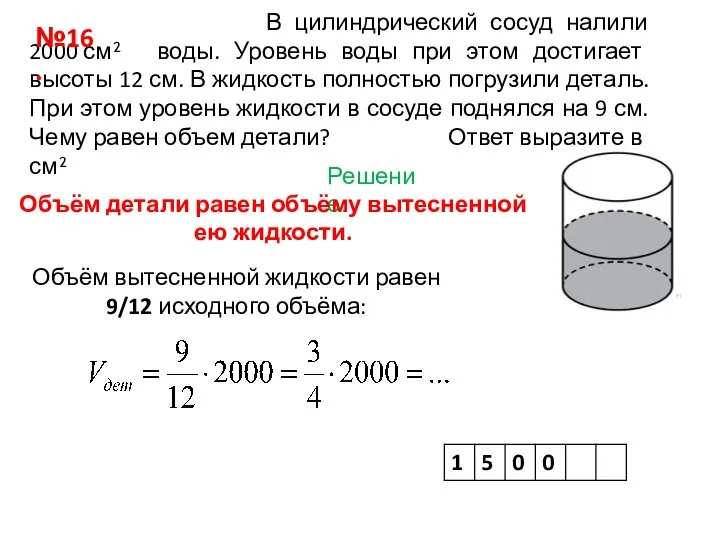
В цилиндрический сосуд налили 2000 см² воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см²
Объём вытесненной жидкости равен 9/12 исходного объёма:
№16.
Решение.
Объём детали равен объёму вытесненной ею жидкости.

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого?
Ответ выразите в см.
№16.
Решение.
Отсюда высота
Число π — это величина постоянная, объем жидкости
V в данной задаче тоже не изменяется.
То есть, высота уровня жидкости обратно пропорциональна радиусу основания сосуда.
Так как радиус увеличился в 2 раза, то высота уменьшится в 4 раза. ( 2²= 4 )

Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Пусть объём первого цилиндра равен
объём второго
где R₁ R₂ — радиусы оснований цилин­дров, H₁ H₂ — их высоты.
то выразим объём второго цилиндра через объём первого:
№16.
Решение.
Т.к.

Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
№16.
Решение.
Т.к.
Пусть объёмы первой и второй кружек равны

№16.
Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй кружки больше объёма первой?
Решение.
Т.к.
Пусть объёмы первой и второй кружек равны

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π
Площадь боковой поверхности цилиндра
поэтому
№16.
Решение.

Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
№16.
Решение.
Решение.
Площадь боковой поверхности цилиндра
C– длина окружности основания.
Поэтому S = 2·3 = 6
№16.

В бак, имеющий форму цилиндра, налито 5 л воды. После полного погружения в воду детали, уровень воды в баке поднялся в 1,2 раза. Найдите объём детали.
Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
№16.
Решение.
Объём детали равен объёму вытесненной ею жидкости.
После погружения детали в воду объём стал равен
5 · 1,2 = 6 литров,
поэтом объём детали равен 6 − 5 = 1 л = 1000 см3.

Вода в сосуде цилиндрической формы находится на уровне h = 40cм. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого ра­диус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.
Объём воды, налитой в цилиндр, высотой h и радиусом R равен
V = πR²h
№16.
Решение.
Следовательно, при увеличении радиуса цилиндра в 2 раза, при неизменном объёме,
значит, вода во втором цилиндре достигнет уровня
h₂= 40 : 4= 10 см.
высота стола воды окажется в 2²= 4 раза меньше,