Содержание
- 2. «Функция, как правило, определяется для тех значений аргумента, какие для данной задачи представляют реальное значение» Хинчин
- 3. sint = 0,5 sint = 0,3 При каких значениях t верно равенство? , t=?
- 4. Обратные тригонометрические функции
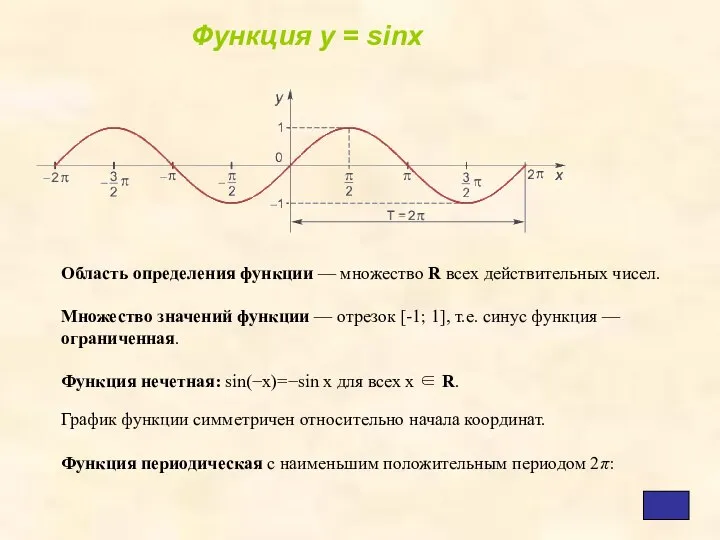
- 5. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1],
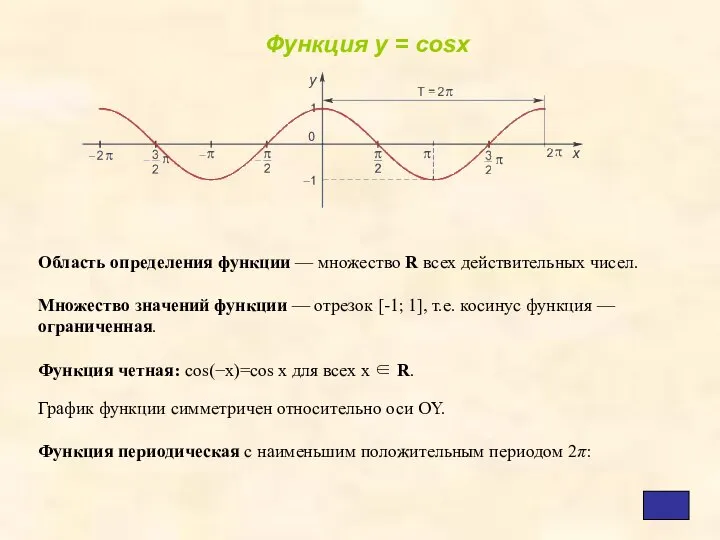
- 6. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1],
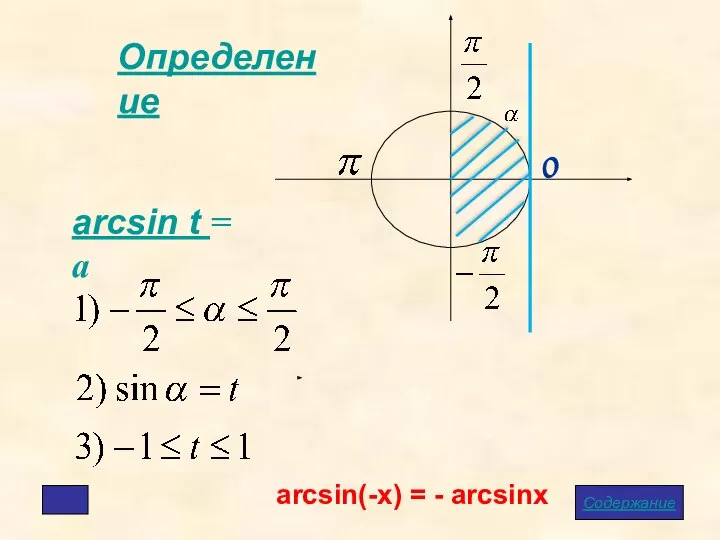
- 7. Определение arcsin t = a arcsin(-x) = - arcsinx Содержание
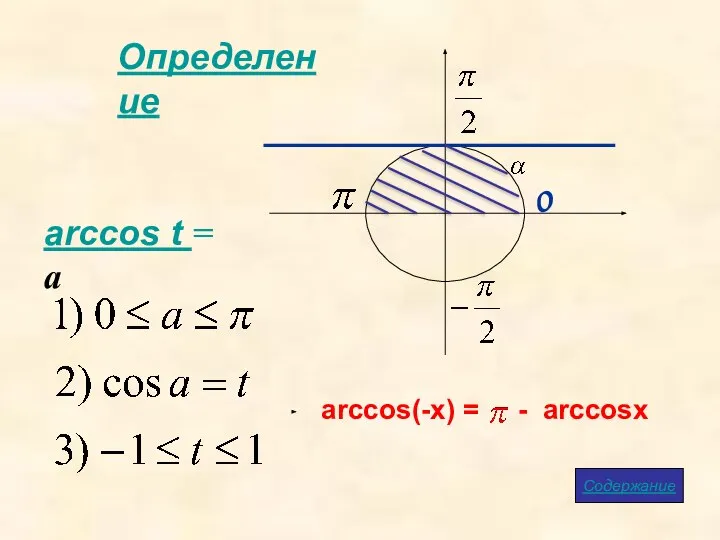
- 8. Определение arccos t = a Содержание arccos(-x) = - arccosx
- 9. Определение arctg t = a Содержание
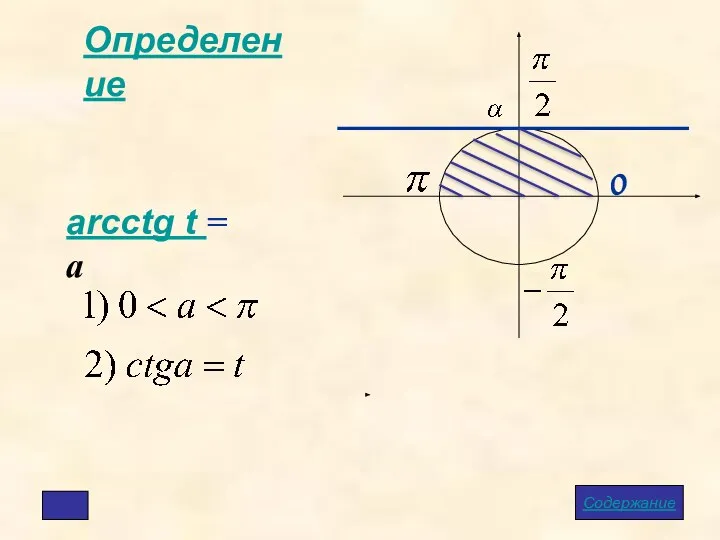
- 10. Определение arcctg t = a Содержание
- 11. у = arcsinx Содержание х 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок ; 3)Функция у
- 12. у=arccos x Содержание 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция у = arcсos x
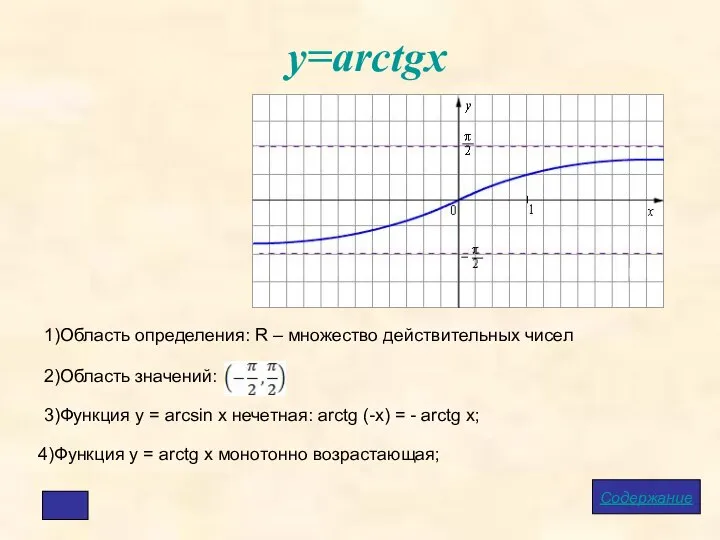
- 13. у=arctgx Содержание 1)Область определения: R – множество действительных чисел 2)Область значений: 3)Функция у = arcsin x
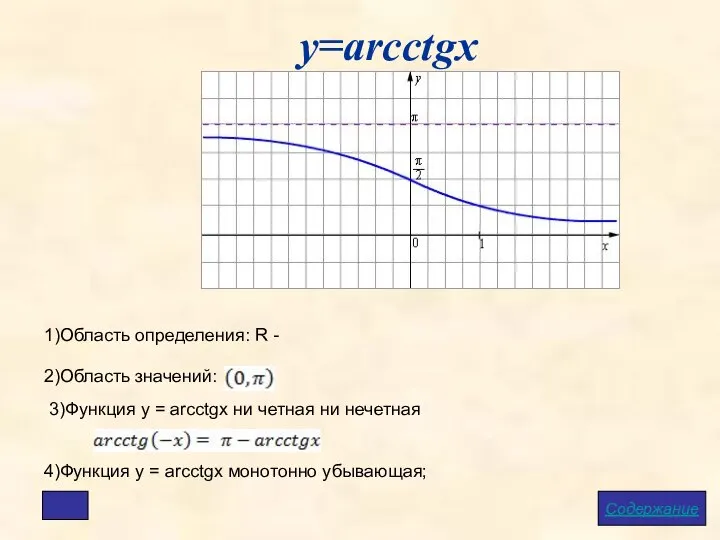
- 14. у=arcctgx Содержание 1)Область определения: R - 2)Область значений: 4)Функция у = arcсtgx монотонно убывающая; 3)Функция у
- 15. Обратные тригонометрические функции
- 16. «Функция, как правило, определяется для тех значений аргумента, какие для данной задачи представляют реальное значение» Хинчин
- 17. учащиеся должны знать определения арксинуса, арккосинуса, арктангенса, арккотангенса, графики этих функций, свойства аркфункций, связь с тригонометрическими
- 18. Работаем устно Содержание arcsin(-x) = - arcsinx arccos(-x) = - arccosx
- 19. Работаем устно Имеет ли смысл выражение? Содержание
- 20. Работаем устно Найдите значения выражений: Содержание
- 21. Работаем устно Содержание arctg(-x) = - arctgx arcctg(-x) = - arcctgx
- 22. Свойства аркфункций
- 24. Формулы связывающие обратные тригонометрические функции
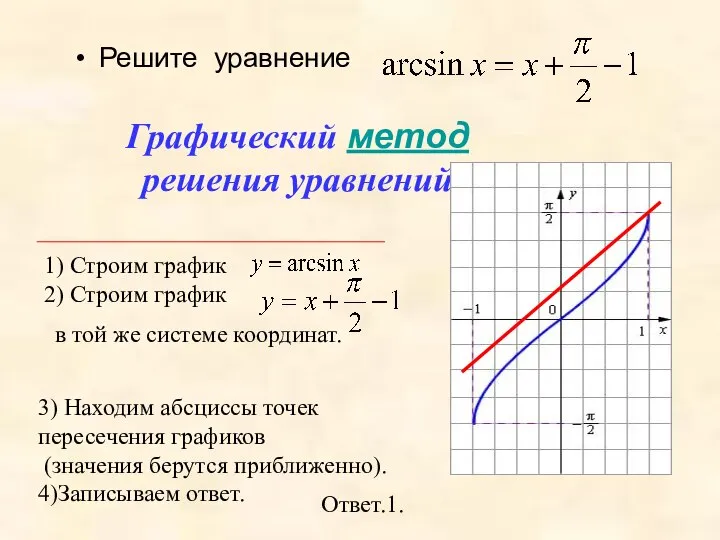
- 25. Решите уравнение Ответ.1. 3) Находим абсциссы точек пересечения графиков (значения берутся приближенно). 4)Записываем ответ. Графический метод
- 26. Функционально-графический метод решения уравнений Пример: решите равнение 3) Уравнение f(x)=g(x) имеет не более одного корня. 4)
- 28. Скачать презентацию



![у = arcsinx Содержание х 1)Область определения: отрезок [-1; 1]; 2)Область значений:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1182298/slide-10.jpg)
![у=arccos x Содержание 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1182298/slide-11.jpg)











 Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2 Математика вокруг нас
Математика вокруг нас Комбинаторика
Комбинаторика Старинные задачи на дроби
Старинные задачи на дроби Умножение нуля и единицы
Умножение нуля и единицы Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Правильные многогранники вокруг нас
Правильные многогранники вокруг нас Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Решение примеров и простых задач в пределах 10
Решение примеров и простых задач в пределах 10 Сечения куба плоскостью
Сечения куба плоскостью координаты вектора
координаты вектора Системы линейных уравнений СЛУ
Системы линейных уравнений СЛУ Геометрическая прогрессия
Геометрическая прогрессия Луч и отрезок
Луч и отрезок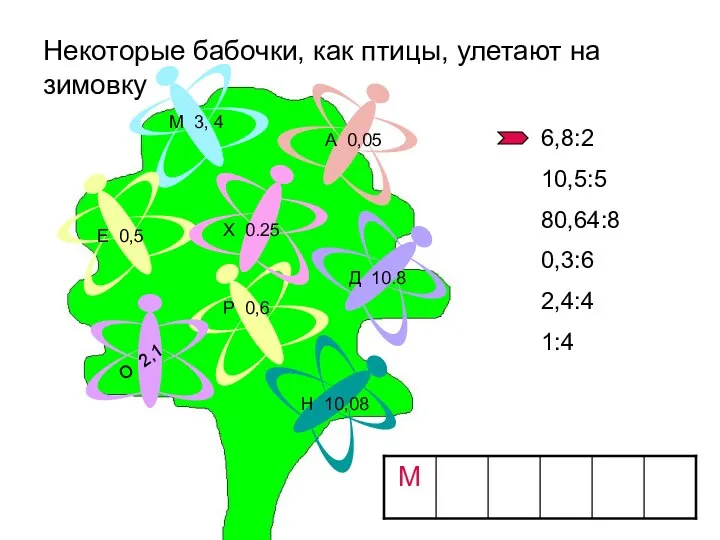 Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку
Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку Многочлен. Решить задачу
Многочлен. Решить задачу Презентация на тему Решение текстовых задач различными способами
Презентация на тему Решение текстовых задач различными способами  Многогранники. Задания
Многогранники. Задания Координаты вектора
Координаты вектора Координатная плоскость
Координатная плоскость Решение логарифмических неравенств
Решение логарифмических неравенств Среднее арифметическое
Среднее арифметическое Презентация на тему Решение задач по теме "Пирамида" 10 класс
Презентация на тему Решение задач по теме "Пирамида" 10 класс  Прямой угол
Прямой угол Вектор. Равенство векторов
Вектор. Равенство векторов Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации