- Главная
- Математика
- Тригонометрические формулы

Содержание
Слайд 2Формулы сложения:
Формулы сложения – это та, группа формул которую нужно знать
Формулы сложения:
Формулы сложения – это та, группа формул которую нужно знать

наизусть. Но для их запоминания можно тоже воспользоваться ассоциативным приемом. У косинуса функции одноименные:
cos ( α - β ) = cos α cos β + sin α sin β;
cos ( α + β ) = cos α cos β - sin α sin β;
а у синуса разноименные:
sin (α + β) = sin α cos β + cos α sin β;
sin (α - β) = sin α cos β - cos α sin β.
Не все в нашей жизни бывает «гладко» за белой полосой идет черная, и наоборот. Так и у наших функций, если функции идут одноименные, то знаки
не совпадают, а если разноименные, то совпадают.
cos ( α - β ) = cos α cos β + sin α sin β;
cos ( α + β ) = cos α cos β - sin α sin β;
а у синуса разноименные:
sin (α + β) = sin α cos β + cos α sin β;
sin (α - β) = sin α cos β - cos α sin β.
Не все в нашей жизни бывает «гладко» за белой полосой идет черная, и наоборот. Так и у наших функций, если функции идут одноименные, то знаки
не совпадают, а если разноименные, то совпадают.
Слайд 3Формулы сложения:
Формулы сложения:

- Предыдущая
Приближенные формулы Лапласа и ПуассонаСледующая -
Искусство блокадного Ленинграда Скалярное произведение в евклидовом и унитарном пространстве
Скалярное произведение в евклидовом и унитарном пространстве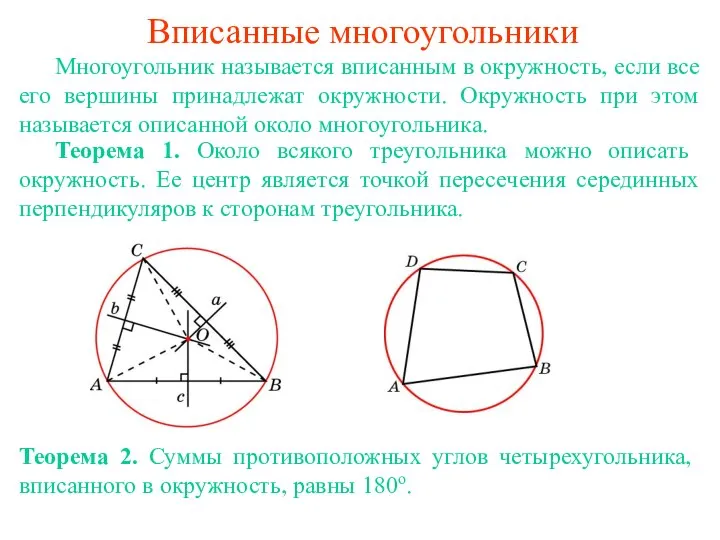 Вписанные и описанные многоугольники
Вписанные и описанные многоугольники Приведение матрицы к жордановой форме
Приведение матрицы к жордановой форме математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Эконометрика. Лекция 2
Эконометрика. Лекция 2 Презентация на тему Сечения
Презентация на тему Сечения  Изображение пространственных фигур
Изображение пространственных фигур Статистика
Статистика Угол между прямой и плоскостью
Угол между прямой и плоскостью Презентация на тему Задачи с практическим содержанием по теме "Арифметическая и геометрическая прогрессии"
Презентация на тему Задачи с практическим содержанием по теме "Арифметическая и геометрическая прогрессии"  Зачем мы изучаем алгебру?
Зачем мы изучаем алгебру? Истинностные задачи
Истинностные задачи Девиз урока: «Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и
Девиз урока: «Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и Экстремумы (1)
Экстремумы (1) Логарифмическая функция
Логарифмическая функция 8 класс
8 класс Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости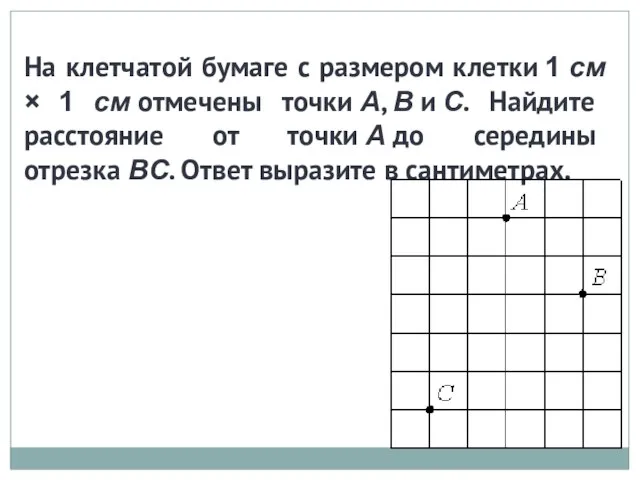 Решение задач
Решение задач Занимательная геометрия. Треугольник - три угла
Занимательная геометрия. Треугольник - три угла Проценты
Проценты Элементы комбинаторики
Элементы комбинаторики Сложение и умножение чисел
Сложение и умножение чисел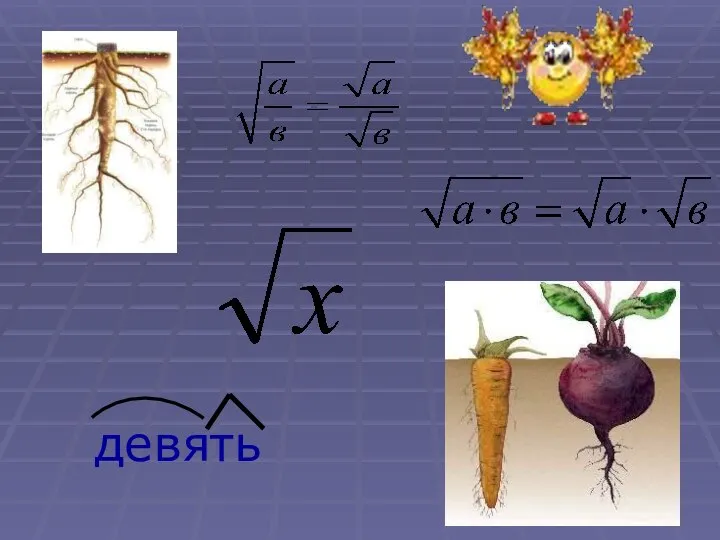 Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5)
Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5) 6. СЛАУ. Методы решения (1)
6. СЛАУ. Методы решения (1) От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Плоскости. Лекция 3
Плоскости. Лекция 3 Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса