Методы измерений. Лекция 2

Зависимость между результатом измерения Y и измеряемой величиной X при прямом измерении характеризуется уравнением Y = X, т. е. значение измеряемой величины принимается равным полученному результату
Косвенное измерение - измерение, при котором искомое значение величины определяют на основании результатов прямых измерений других величин, функционально связанных с искомой величиной.
Пример — Определение плотности р тела цилиндрической формы по результатам прямых измерений массы m, высоты h и диаметра цилиндра d, связанных с плотностью уравнением :
Cовокупные измерения – это проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
Число уравнений должно быть не меньше числа величин.
Пример: нахождение значений сопротивлений резисторов, соединенных по схеме треугольника. Здесь измеряют сопротивления между каждой парой вершин треугольника и получают систему уравнений

Решая систему уравнений получим:
Совместные измерения – это проводимые одновременно измерения двух или нескольких не одноименных величин для определения зависимости между ними.
Пример: нахождение зависимости сопротивления резистора от температуры. Для этого используют известное выражение:
где сопротивление резистора при некоторой температуре t; - сопротивление резистора при температуре 0 0С; - температурный коэффициент сопротивления;
t – температура.

Решая систему из двух уравнений, составленных для двух значений температуры:
найдем значения и
Совокупные и совместные измерения есть обобщение косвенных измерений на случай нескольких величин.
По числу измерений последние подразделяются на: однократное и многократное.
По характеру зависимости измеряемой величины от времени измерения разделяются: на статические и динамические.
Статические - измерения при которых измеряемую величину принимают в соот-ветствии с конкретной измерительной задачей за неизменную на протяжении времени измерения;
Динамические – измерения при которых измеряемая величина изменяется по размеру в процессе измерения.
Например, измерение длины детали при нормальной температуре – статическое измерение, измерение электрического напряжения в тяговой сети – динамическое. Термин «динамическое» относится к измеряемой величине. Однако, очевидно, что для оценки точности результатов динамических измерений необходимо знание динамических свойств средств измерений.

По условиям, определяющим точность результатов, измерения бывают равноточные и неравноточные.
Равноточные измерения – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью
Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях. Ряд неравноточных измерений обрабатывают с учетом веса отдельных измерений.
Ряд измерений (результатов измерений) – значения одной и той же величины, полученные из следующих друг за другом измерений. Среднее значение из ряда неравноточных измерений определяется с учетом веса каждого единичного измерения. Среднее взвешенное значение иногда называют средним весовым.
По способу выражения результатов измерения различают абсолютные и относи-тельные измерения.
Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительные измерения – измерения отношения величины к одноименной величине, играющей роль единицы, или измерения изменения величины по отноше-нию к одноименной величине, принимаемой за исходную.
Например, измерение силы – абсолютное измерение, т. к. оно основано на измерении основной величины – массы « » в точке измерения массы.

По приему (приемам) сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений разделяются на: методы непосредственной оценки и методы сравнения c мерой.
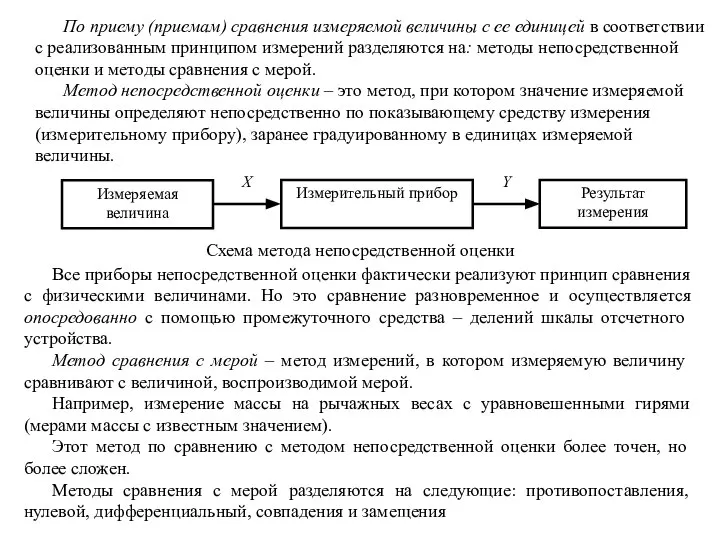
Метод непосредственной оценки – это метод, при котором значение измеряемой величины определяют непосредственно по показывающему средству измерения (измерительному прибору), заранее градуированному в единицах измеряемой величины.
Все приборы непосредственной оценки фактически реализуют принцип сравнения с физическими величинами. Но это сравнение разновременное и осуществляется опосредованно с помощью промежуточного средства – делений шкалы отсчетного устройства.
Метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
Например, измерение массы на рычажных весах с уравновешенными гирями (мерами массы с известным значением).
Этот метод по сравнению с методом непосредственной оценки более точен, но более сложен.
Методы сравнения с мерой разделяются на следующие: противопоставления, нулевой, дифференциальный, совпадения и замещения
Схема метода непосредственной оценки

Различают методы одновременного сравнения, когда мера и измеряемая величина воздействуют на измерительный прибор одновременно, и разновременного сравнения, когда воздействие измеряемой величины и меры на измерительный прибор разнесено во времени. Кроме того, сравнение может быть непосредственным и опосредованным. В первом случае измеряемая величина и мера непосредственно воздействуют на прибор сравнения, а во втором – через другие величины, однозначно связанные с известной и измеряемой величинами.
Методы одновременного сравнения: противопоставления, нулевой, дифференци-альный и совпадения.
Методы разновременного сравнения: замещения.
Метод противопоставления – метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами.

Измеряемая величина Х и мера X0 воздействуют на два входа прибора сравнения. Результирующий эффект воздействия определяется разностью этих величин:
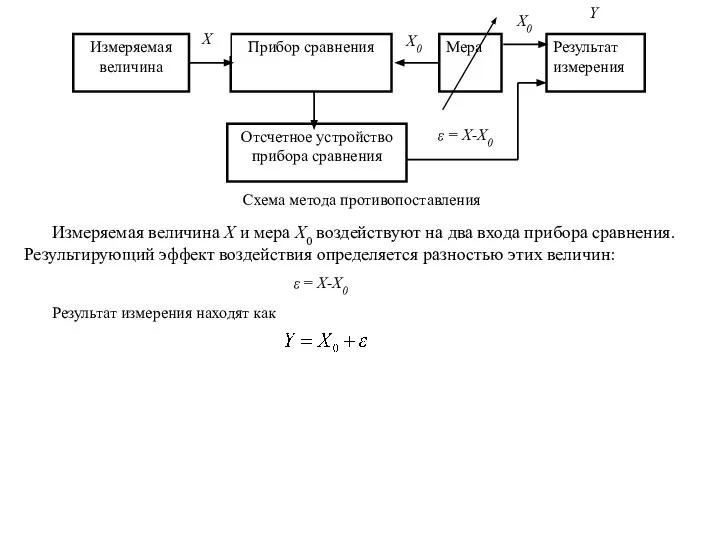
Результат измерения находят как
ε = X-X0

Необходима точная многозначная мера и несложные устройства сравнения.
Пример: взвешивание груза на равноплечих весах с помещением измеряемой массы и уравновешивающих её гирь на двух чашках весов и с полным уравновешиванием весов.
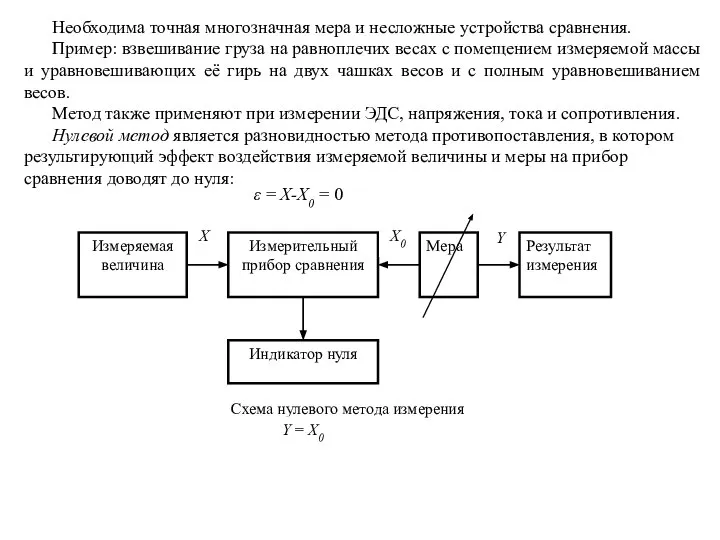
Метод также применяют при измерении ЭДС, напряжения, тока и сопротивления.
Нулевой метод является разновидностью метода противопоставления, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля:
ε = X-X0 = 0
Y = X0

На индикатор нуля воздействует разность величин, поэтому его предел измерения может быть выбран меньшим, а чувствительность большей, чем у прибора для измерения X методом непосредственной оценки.
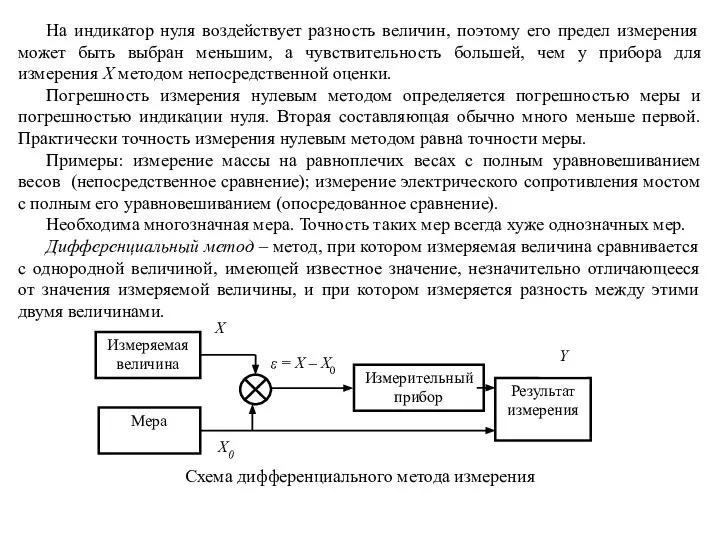
Погрешность измерения нулевым методом определяется погрешностью меры и погрешностью индикации нуля. Вторая составляющая обычно много меньше первой. Практически точность измерения нулевым методом равна точности меры.
Примеры: измерение массы на равноплечих весах с полным уравновешиванием весов (непосредственное сравнение); измерение электрического сопротивления мостом с полным его уравновешиванием (опосредованное сравнение).
Необходима многозначная мера. Точность таких мер всегда хуже однозначных мер.
Дифференциальный метод – метод, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.
X
Схема дифференциального метода измерения

Мера имеет постоянное значение разность измеряемой величины и меры
не равна нулю и измеряется измерительным прибором. Результат измерения находятся как
Измерительный прибор измеряет не всю величину Х, а только ее часть, что позволяет уменьшить влияние на результат измерения погрешность измерительного прибора, причем влияние погрешности измерительного прибора тем меньше, чем меньше разность
Пример: при измерении, например, напряжения U = 97 B вольтметром непосред-ственной оценки с пределом измерения 100 В и допущенной относительной погреш-ностью измерения этого напряжения 1 % (0,01) получают абсолютную погрешность измерения В.
При измерении этого напряжения дифференциальным методом с использованием образцового источника напряжения В разность напряжений
В.
измеряют уже вольтметром с пределом измерения 3 В. Пусть его относительная погрешность измерения будет также равна 1 % . Это дает абсолютную погрешность измерения напряжения: В.
Приведя эту погрешность к измеряемому напряжению U, получим относительную погрешность измерения напряжения:

Погрешность приблизительно в 30 раз меньше, чем при измерении напряжения методом непосредственной оценки. Данное увеличение точности измерения объяс-няется тем, что в первом случае прибором была измерена почти вся величина с отно-сительной погрешностью в 1 % , а во втором случае измеряется не вся величина, а только ее 1/30 часть.
Метод совпадений (или метод «нониуса») представляет собой метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов. Этот метод применяется в случаях, когда измеряемая величина меньше цены деления заданной меры. При этом применяют две меры с разными ценами деления, которые отличаются на размер оцениваемого разряда отсчетов.
Примером измерения методом совпадения служит: – измерение длины детали с помощью штангенциркуля.

Метод замещения - это метод, в котором измеряемую величину замещают мерой с известным значением величины.
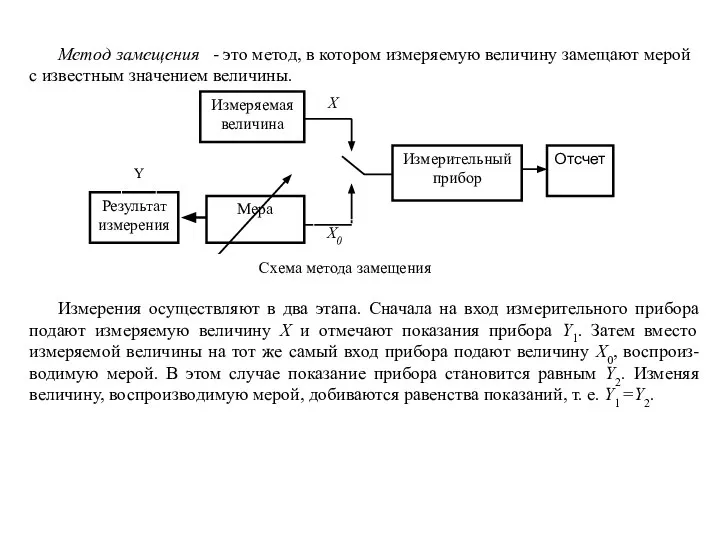
Измерения осуществляют в два этапа. Сначала на вход измерительного прибора подают измеряемую величину Х и отмечают показания прибора Y1. Затем вместо измеряемой величины на тот же самый вход прибора подают величину X0, воспроиз-водимую мерой. В этом случае показание прибора становится равным Y2. Изменяя величину, воспроизводимую мерой, добиваются равенства показаний, т. е. Y1 =Y2.