Основы теории множеств

Понятие множества
Понятие множества является основным, неопределяемым понятием, поэтому его можно только пояснить.
Учебные группы: 589-1, 589-2, 589-3

Интуитивное определение «множества» принадлежит немецкому математику Георгу Кантору (1845-1918).
Георг Кантор

Под множеством S будем понимать любое собрание определенных и различимых между собою объектов, мыслимое как единое целое.
Эти объекты называются элементами множества S.

Существенным в определении множества, данном Кантором, является то, что само собрание предметов рассматривается как один предмет и
мыслится как единое целое.
Что касается самих предметов, которые входят во множество, то относительно них существует значительная свобода.

Это может быть множество студентов в аудитории, множество целых чисел, множество точек плоскости.
Важно, что канторовская формулировка позволяет рассматривать множества, элементы которых по той или иной причине нельзя точно указать (например, множество простых чисел, множество белых носорогов и т. п.).
Не следует думать, что множество обязательно должно содержать в каком-то смысле однородные объекты. Можно объединить в одно множество и королей, и капусту.

Интуитивные принципы Кантора

Принцип абстракции
Любой одноместный предикат A(x) определяет некоторое множество X, а именно множество тех и только тех предметов x, для которых A(x) – истинное предложение.
Принцип объемности
Множества A и B считаются равными, если они состоят из одних и тех же элементов.
(Часто это выражают словами: «Множества равны, если их характеристические свойства эквивалентны»).
Записывают A=B, если A и B равны,
в противном случае – A≠B .

Пример.Проиллюстрируем принцип объёмности.
Множество A всех положительных чётных чисел равно множеству B положительных целых чисел, представимых в виде суммы двух положительных нечетных чисел.
Действительно, если x∈A, то для некоторого целого положительного числа m имеем x = 2m; тогда x = (2m – 1) + 1, т. е. x∈B.
Если x∈B, то для некоторых целых положительных p и q имеем x = (2p – 1) + (2q -1) = 2(p + q –1), т.е. x∈A.
*

Обозначение конечных множеств

Множество, элементами которого являются объекты a1, a2,…, an и только они, обозначают {a1, a2,…, an}.
Его определение через характеристическое свойство:
{a1, a2,…, an} = {x | x = a1∨ x ,…, a1 ∨ …∨ x = an}.
Исходя из этого тождества, можно видеть, в частности, что
{a, b} = {b,a}, {a, a} = {a}.

В общем случае порядок, в котором элементы расположены при описании множества, не имеет значения;
не имеет значения также возможность неоднократного повторения одних и тех же элементов при описании множества.

ещё одна тонкость:
Нужно строго различать x и {x}.
Первое выражение обозначает сам элемент,
а второе – множество, содержащее этот один элемент.

А= {x, c, s, v, t}
B = {t, c, v, s, t, c, x, }
A = B ?

Отношение принадлежности и характеристическое свойство

Символом ∈ обозначается отношение принадлежности.
Запись x∈S означает, что элемент x принадлежит множеству S.
Если элемент x не принадлежит множеству S, то пишут x∉S.
Множество всех объектов, обладающих свойством A(x), обозначается {x | A(x)}.
Если Y = {x | A(x)}, то A(x) называется характеристическим свойством множества Y.
По определению Y, выполнена следующая эквивалентность:
∀y(y∈Y ~ A(y)).

Подмножества множества

Множество A есть подмножество множества B (обозначается A⊆B), если каждый элемент A есть элемент B; т.е. если x∈A, то x∈B.
Отношение ⊆ между множествами называется отношением включения.
В частности, каждое множество есть подмножество самого себя.
Если A не является подмножеством B, то, значит, существует элемент A, не принадлежащий B.

Определить:
{1, 2, 3} ⊆ {1, 2, 3, 4}?
{1, 2, 5} ⊆ {1, 2, 3, 4}?

Если A = {x| x – футболист факультета}, B = {x|, x спортсмен факультета}, а C = {x| x – самый сильный
математик факультета}, то
A⊆B ?
C является подмножеством B?
запомнить:
а) X⊆X;
б) если X⊆Y, Y⊆Z, то X⊆Z;
в) если X⊆Y и Y⊆X , то X=Y.

Если множество A есть собственное подмножество множества B, то пишут (обозначается A⊂B), если A ⊂ B и A≠B.
Если A не является собственным подмножеством B, то это означает, что либо A=B, либо существует элемент A, не принадлежащий B.
Отношение ⊂ между множествами называется отношением строгого включения.

Подмножества множества (продолжение)
*

Множество всех подмножеств A называется множеством-степенью и обозначается P(A).
Из определения следует, что X∈P(A), тогда и только тогда, когда X⊆A.
Пример. Если A = {1,2,3}, то P(A) = {∅, {1}, {2},{3},
{1, 2}, {1, 3}, {2,3}, A}.
В дальнейшем неоднократно будем пользоваться утверждением, что если множество A состоит из n элементов, то множество P(A) состоит из 2n элементов.
*

Доказательство равенства множеств A и B состоит из двух этапов:
1) Доказать, что A есть подмножество B.
2) Доказать, что B есть подмножество A.
Множество, не содержащее элементов, называется пустым и обозначается ∅.
Пустое множество есть подмножество любого множества.
Очевидно, что пустое множество задается тождественно ложным характеристическим свойством, и соответственно все пустые множества равны.
Поэтому считается, что множество квадратных кругов равно множеству белых ворон.

Классификация чисел
САМОСТОЯТЕЛЬНО изучить тему:

Натуральные числа - число натурального ряда 1, 2, 3, 4, ..и так до бесконечности; единица и все числа, которые можно получить в результате сложения единиц.
Натуральные числа это 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 и так далее.
Их используют при подсчёте предметов.
Ненатуральные числа - это все другие числа (дробные, отрицательные, числа, получаемые после извлечения корня, значения тригонометрических функций, логарифмы)

Действительные числа (R) –действительное число или как его еще называют вещественное число - это любое положительное число, отрицательное число или нуль.
Иррациональное число (I), это число, которое в десятичном виде можно записать только непериодической бесконечной десятичной дробью. В том к ним относятся число Пи и Экспонента.
(Иррациональные числа не представимы в виде обыкновенной дроби).

Рациональные числа (Q) - Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью , где числитель m — целое число, а знаменатель n — натуральное число.

Комплексное число это упорядоченная пара чисел Z=(x,y) , где первое число это действительная часть,
второе число- мнимая часть числа С.
Комплексные числа (C)

Для компл. чисел определили операции сложения и умножения
Z1+Z2=(x1,y1)+(x2,y2)= (x1+x1, y1+y2) ;
Z1*Z2=(x1,y1)*(x2,y2)=(x1*x2-y1*y2, x1*y2+y1*x2) .
Для этих действий не нарушаются всякие законы, типа переместительного и пр.
Поэтому ими можно пользоваться.

Как и было написано сначала (Z=(0,y) )
Проверим это :
Действительные числа можно представлять в виде z=(x,0).
Мнимые в виде Z=(0,y) или Z= i*y , где i- мнимая единица. i=(0,1).
Проверка.
Z=(0,1)* (0,y)= (0*y-1*0, 0*0+1*y)= (0,y) .

Пример. Пусть A обозначает множество чётных чисел, Q – множество рациональных чисел, R – множество действительных чисел, а C – множество комплексных чисел. Тогда выполняются строгие включения A⊂Q, Q⊂R, R⊂C.
Очевидно, если X⊂Y, Y⊂Z, то X⊂Z.
Не надо смешивать отношения принадлежности и включения. Например, имеем {1}∈{{1}} и {1} не является подмножеством {{1}}, с другой стороны 1∉{{1}}, так как единственным элементом множества {{1}} является {1}.

Множество чётных чисел (А) является подмножеством комплексных чисел (С) ?
Пример 2.
Решить аналитически:
Множество чётных чисел (А)

Решение примера 2.
Обозначим классы чисел:
R – множество действительных чисел.
Q - множество рациональных чисел.
С - множество комплексных чисел.
Тогда :
А Q;
∩
∩
R = { {Q}, {Ip}}
∩
А С.
∩
Знаем —
Q R;
R C ;

Операции над множествами

Получения новых множеств из уже существующих
Объединением множеств A и B называется множество A∪B, все элементы которого являются элементами множества A или B:
A∪B = {x | x∈A ∨ x∈B}.
Пересечением множеств A и B называется множество A∩B, элементы которого являются элементами обоих множеств A и B:
A∩B = { x | x∈A & x∈B}.
Выполняются включения A∩B ⊆ A ⊆ A∪B и A∩B ⊆ B ⊆A∪B.
Говорят, что два множества не пересекаются, если их пересечение – пустое множество.
Относительным дополнением множества A до множества X называется множество X\A всех тех элементов множества X, которые не принадлежат множеству A:
X\A = {x | x∈X & x∉A}. (также называют разностью множеств X и A)
Симметрической разностью множеств A и B называется множество A÷B = (A\B) ∪ (B\A). *)
Когда фиксирован универсум U абсолютным дополнением множества A называется множество всех тех элементов x, которые не принадлежат множеству A:
A = { x | x∈U & x∉ A}.
Заметим, что A = U\A. Часто вместо A будем писать ¬A или A’.

Диаграммы Эйлера
Первым стал использовать теперь общепринятые обозначения операций над множествами Джузеппе Пеано (1888 г.).
Для наглядного представления отношений между подмножествами какого-либо универсума используются диаграммы Эйлера. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества.
Часто все множества на диаграмме размещают внутри квадрата, который представляет собой универсум U.
Если элемент принадлежит более чем одному множеству, то на диаграмме области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях.
¬A A∩B A∪B

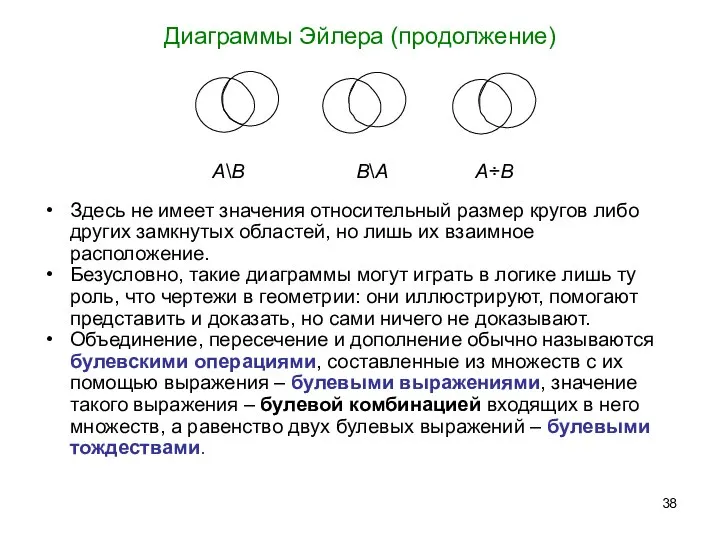
Диаграммы Эйлера (продолжение)
Здесь не имеет значения относительный размер кругов либо других замкнутых областей, но лишь их взаимное расположение.
Безусловно, такие диаграммы могут играть в логике лишь ту роль, что чертежи в геометрии: они иллюстрируют, помогают представить и доказать, но сами ничего не доказывают.
Объединение, пересечение и дополнение обычно называются булевскими операциями, составленные из множеств с их помощью выражения – булевыми выражениями, значение такого выражения – булевой комбинацией входящих в него множеств, а равенство двух булевых выражений – булевыми тождествами.
A\B B\A A÷B

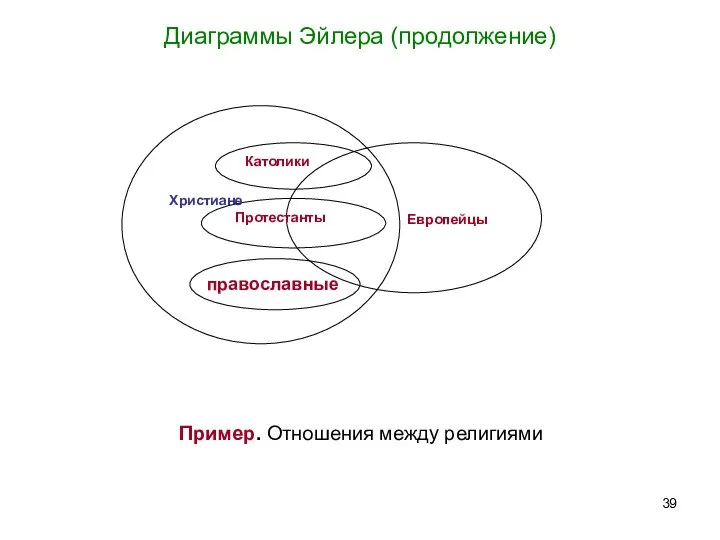
Диаграммы Эйлера (продолжение)
Пример. Отношения между религиями

Булевы выражения
(A∪B∪C)\(C∩B) =
(C÷B)U(A\(A∩B∩C))
(A∩C)∪(B∩C) =
C\ ¬(A∪B)
Джордж Буль

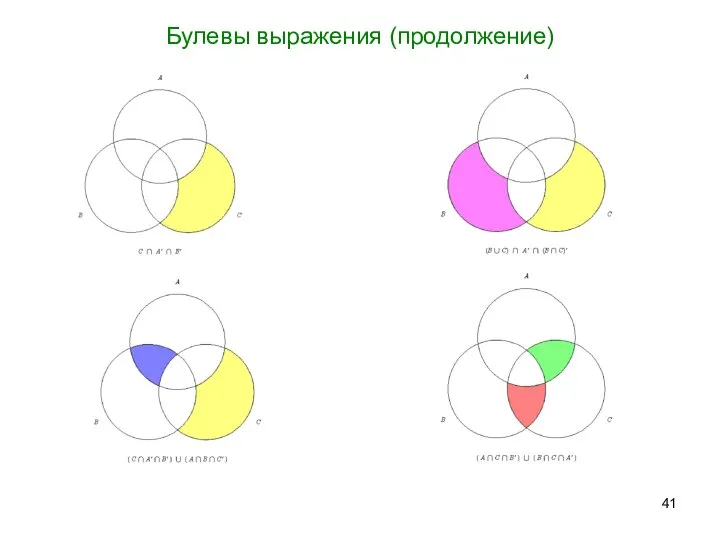
Булевы выражения (продолжение)

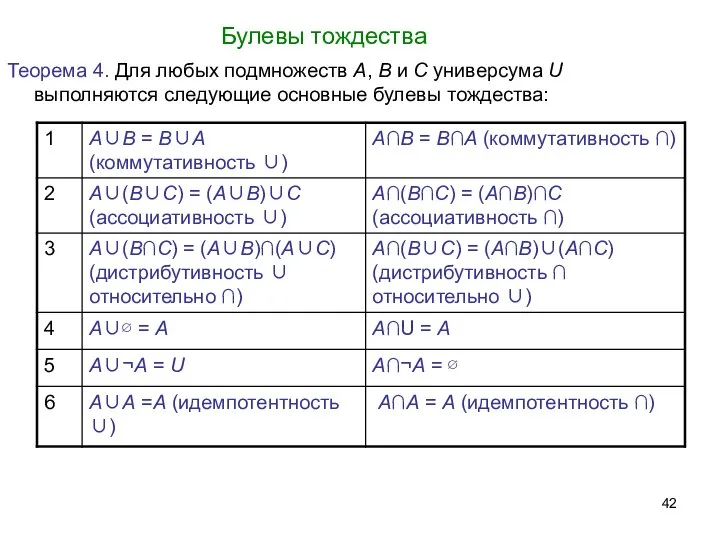
Булевы тождества
Теорема 4. Для любых подмножеств A, B и C универсума U выполняются следующие основные булевы тождества:

Булевы тождества (продолжение)
Теорема 4 (продолжение).
10 A\B = A ∩¬B
Докажем тождество A∪(B∩C) = (A∪B)∩(A∪C) . Сначала покажем, что A∪(B∩C) ⊆ (A∪B)∩(A∪C).
Действительно, если x∈A∪(B∩C), то x∈A или x∈B∩C. Если x∈A, то x∈A∪B и x∈A∪C. Следовательно, x∈(A∪B)∩(A∪C). Если x∈B∩C, то x∈B и x∈C. Отсюда x∈A∪B и x∈A∪C, а значит, x∈(A∪B)∩(A∪C).

ПРИМЕРЫ ДОКАЗАТЕЛЬСТВ

Доказать: A∪(B∩C) = (A∪B)∩(A∪C)
Имеем A∪(B∩C) = {x | x∈A∪(B∩C)} =
(по определению объединения и пересечения множеств)
{x | x∈A ∨ (x∈B & x∈C)} =
(дистрибутивность ∨ относительно &)
{x | (x∈A ∨ x∈B) & (x∈A ∨ x∈C)}= (A∪B)∩(A∪C).

Продолжение
(доказательство справа)

Докажем тождество ¬(A∪B) = ¬A∩¬B .
Пусть x∈¬(A∪B).
Тогда x∈U и x∉A∪B.
Следовательно, x∉A и x∉B.
Отсюда x∈¬A и x∈¬B,
значит, x∈¬A∩¬B.
Итак доказали, что ¬(A∪B)⊆¬A∩¬B.
Пусть теперь, x∈¬A∩¬B.
Тогда x∈¬A и x∈¬B.
Следовательно, x∈U и x∉A и x∉B.
Значит, x∉ A∪B, т.е. x∈¬(A∪B).
Итак, ¬A∩¬B ⊆ ¬(A∪B).

Второй способ доказательства.
Имеем ¬(A∪B) = {x | x∈ ¬(A∪B)} =
(по определению дополнения и объединения)
{ x | x∈U & ¬ ( x∈A ∨ x∈B)} =
(закон де Моргана для ∨)
{ x | x∈U & ¬( x∈A) & ¬( x∈B)} =
(определение дополнения)
{ x | x∈¬A & x∈¬B} = ¬A∩¬B.

Остальные тождества доказываются аналогично. Справедливость этих тождеств можно наглядно проиллюстрировать с помощью диаграмм Эйлера, но это не является доказательством.
С другой стороны, диаграмму вполне можно использовать, чтобы на частном примере опровергнуть какое-нибудь общее утверждение.

Второй способ доказательства.
Имеем ¬(A∪B) = {x | x∈ ¬(A∪B)} =
(по определению дополнения и объединения)
{ x | x∈U & ¬ ( x∈A ∨ x∈B)} =
(закон де Моргана для ∨)
{ x | x∈U & ¬( x∈A) & ¬( x∈B)} =
(определение дополнения)
{ x | x∈¬A & x∈¬B} = ¬A∩¬B.

Теорема 5.
Рассмотрим предложения о произвольных
множествах A и B - (попарно эквивалентны):
A∩B = A
A∪B = B
A⊆B

Доказательство.

Докажем, что из первого предложения
следует второе.
Действительно, так как A ∩ B = A, то достаточно показать, что в этом случае A ⊆ A∩B.
Но если x ∈ A, то x ∈ B, так как A ⊆ B, следовательно, x ∈ A ∩ B.

Докажем, что из второго предложения
следует третье.
Так как A∩B = A, то A∪B = (A∩B)∪B.
По закону поглощения (см. тождества) запишем:
B∪(A∩B) = B.
Отсюда, используя закон коммутативности, получаем A∪B = B.

Докажем, что из третьего предложения следует первое.
Так как A⊆ A∪B, а по условию третьего предложения A∪B = B,
то A⊆B.