Содержание
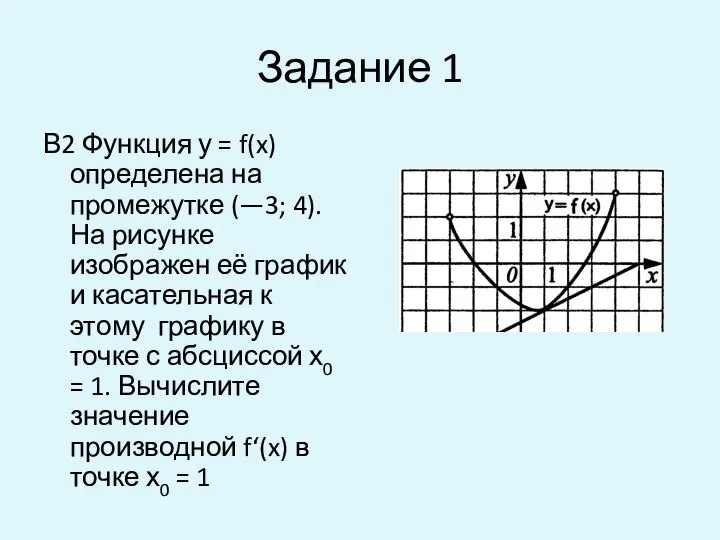
- 2. Задание 1 В2 Функция у = f(x) определена на промежутке (—3; 4). На рисунке изображен её
- 3. Решение задания 1 В данном примере на рисунке по условию задачи изображена касательная к графику у=
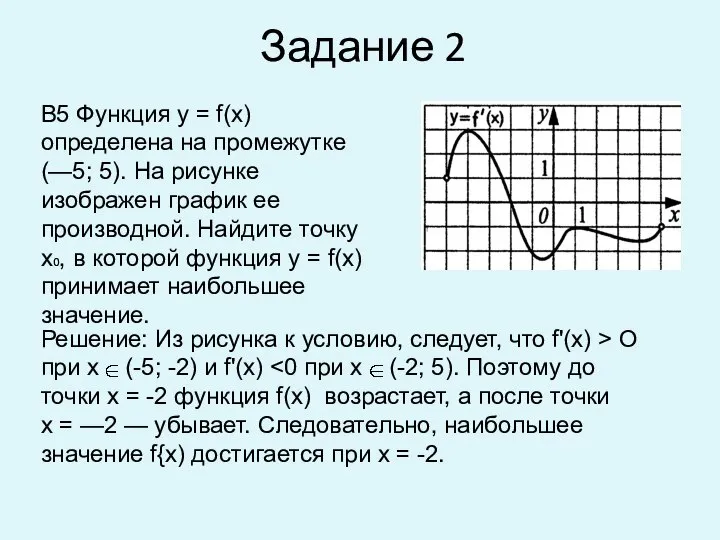
- 4. Задание 2 В5 Функция у = f(x) определена на промежутке (—5; 5). На рисунке изображен график
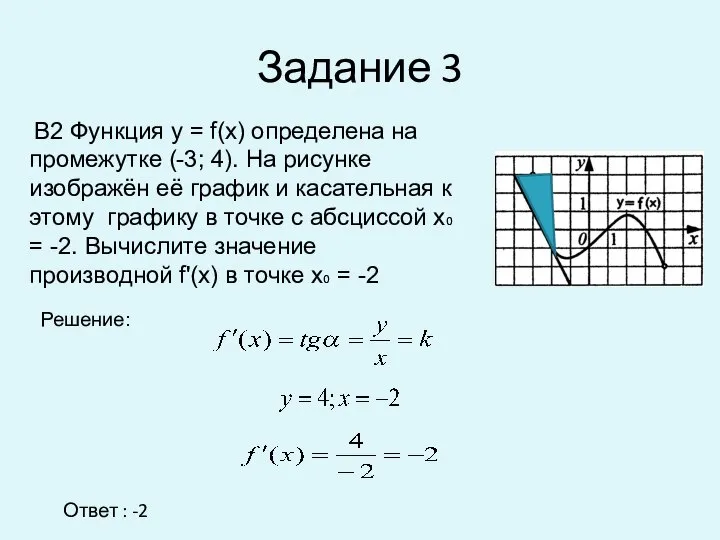
- 5. Задание 3 Ответ : -2 В2 Функция у = f(x) определена на промежутке (-3; 4). На
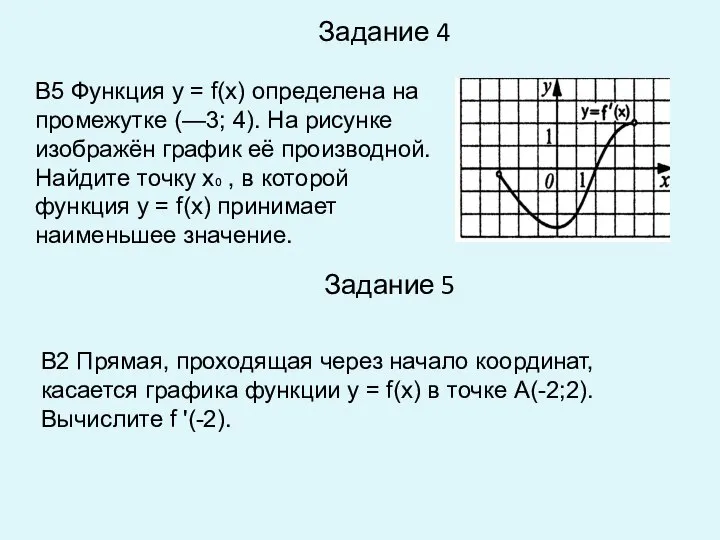
- 6. Задание 4 Задание 5 В5 Функция у = f(x) определена на промежутке (—3; 4). На рисунке
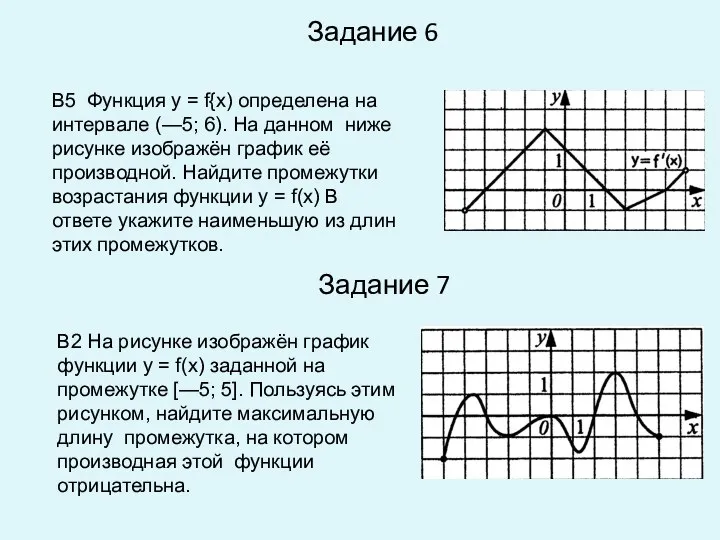
- 7. Задание 6 Задание 7 В5 Функция у = f{x) определена на интервале (—5; 6). На данном
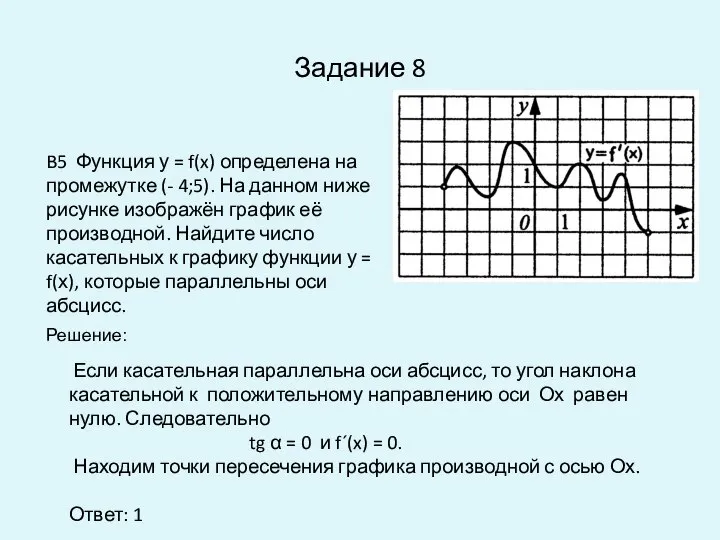
- 8. Задание 8 Если касательная параллельна оси абсцисс, то угол наклона касательной к положительному направлению оси Ох
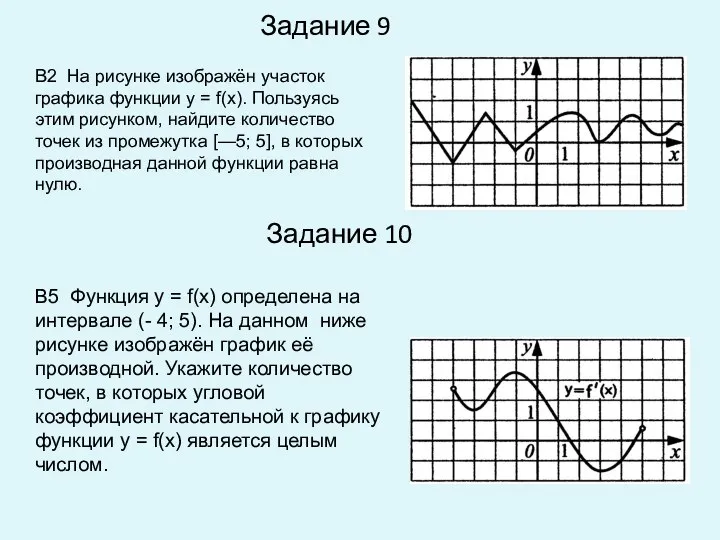
- 9. Задание 9 Задание 10 В2 На рисунке изображён участок графика функции у = f(x). Пользуясь этим
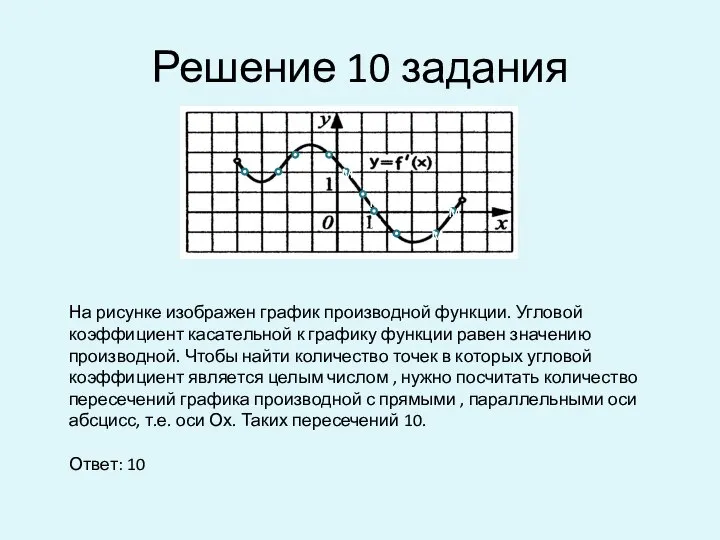
- 10. Решение 10 задания На рисунке изображен график производной функции. Угловой коэффициент касательной к графику функции равен
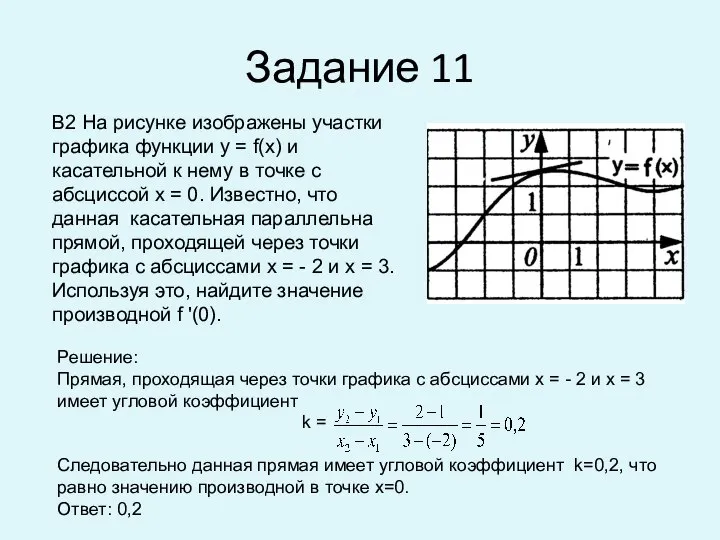
- 11. Задание 11 B2 На рисунке изображены участки графика функции у = f(x) и касательной к нему
- 12. Задание12 85 Известно, что прямая у = 4х - 1 является касательной к параболе у =
- 13. Задания с 13 по 28 для самостоятельной работы
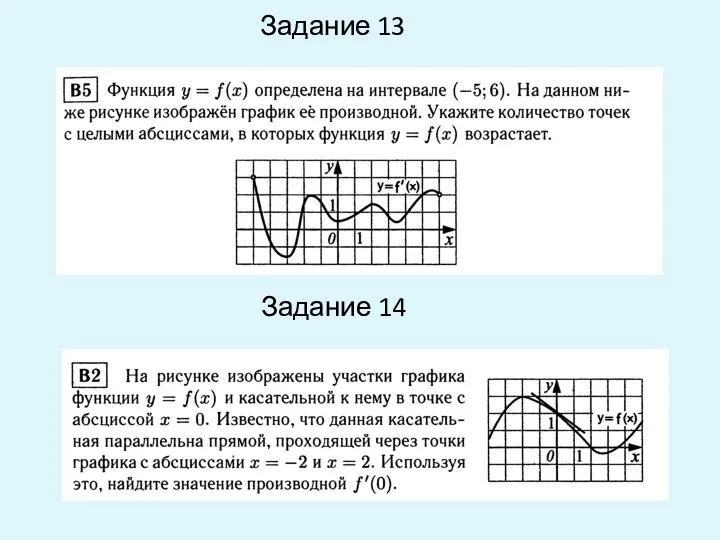
- 14. Задание 13 Задание 14
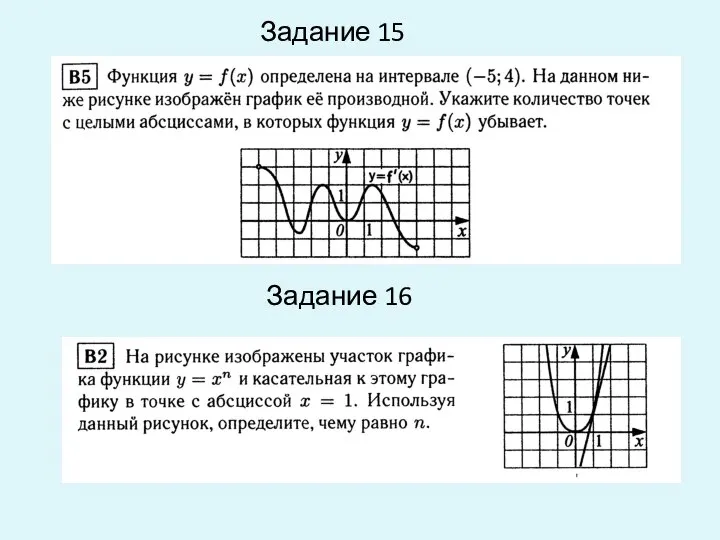
- 15. Задание 15 Задание 16
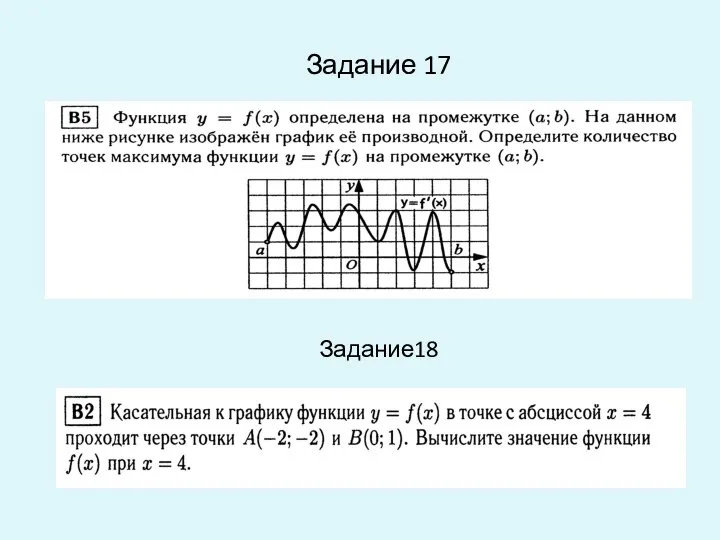
- 16. Задание 17 Задание18
- 17. Задание 19 Задание 20
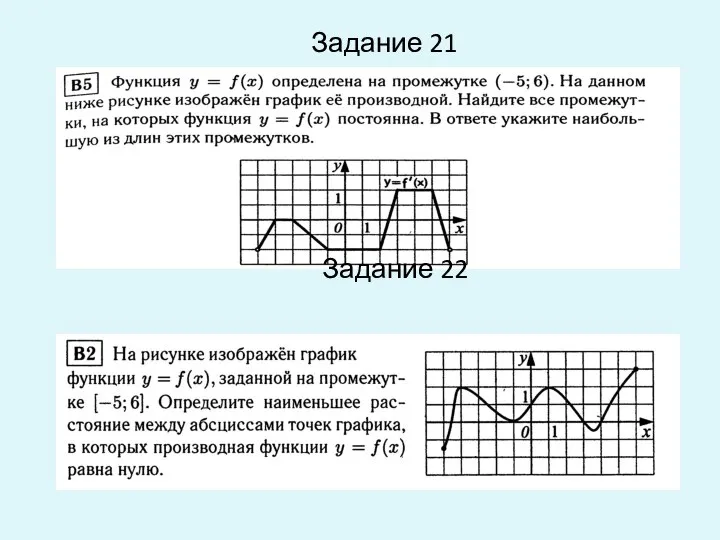
- 18. Задание 21 Задание 22
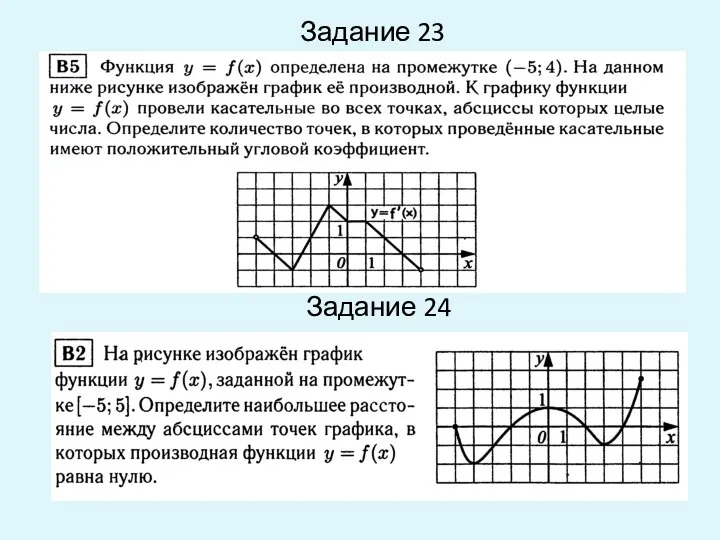
- 19. Задание 23 Задание 24
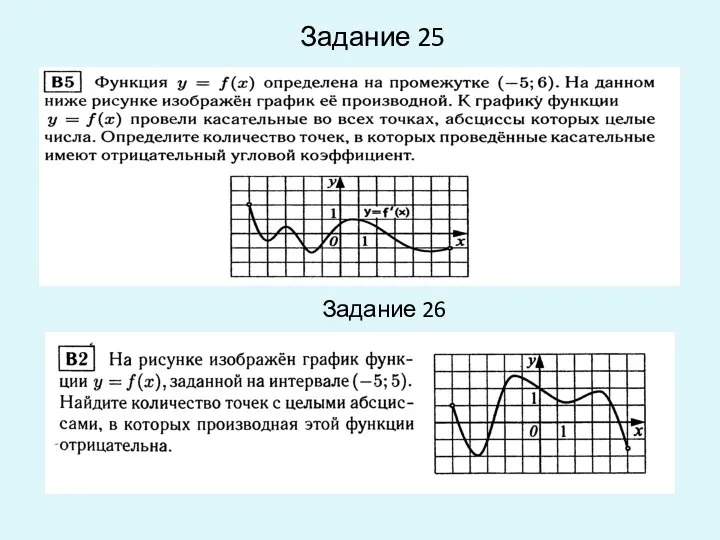
- 20. Задание 25 Задание 26
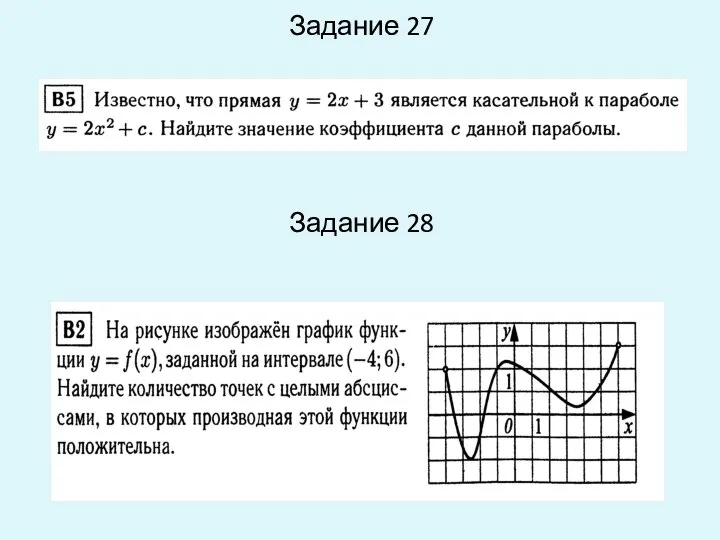
- 21. Задание 27 Задание 28
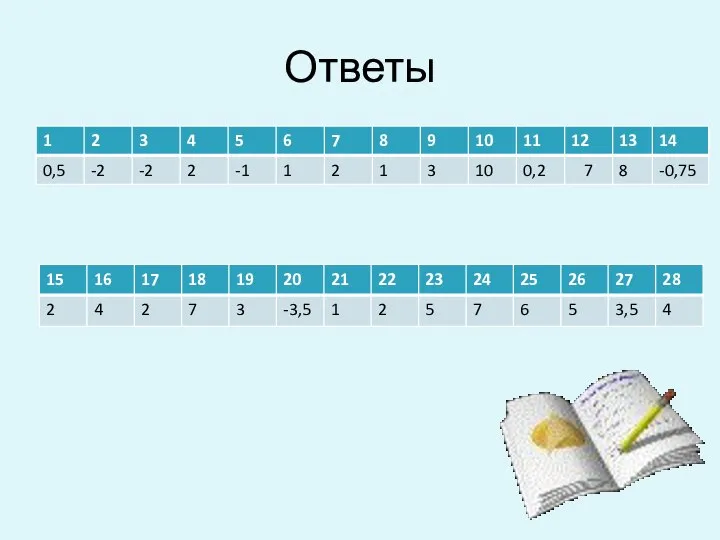
- 22. Ответы
- 24. Скачать презентацию




 Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково
Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково Доли. Устный счет
Доли. Устный счет Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Упрощение выражений. Урок-сказка
Упрощение выражений. Урок-сказка Решение уравнений
Решение уравнений Признаки классификации статистической сводки
Признаки классификации статистической сводки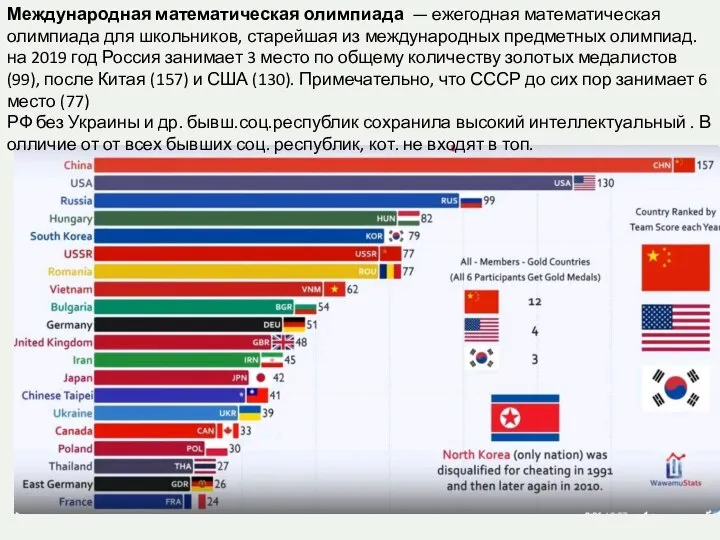 Международная математическая олимпиада
Международная математическая олимпиада Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур Презентация на тему Математический КВН 8 класс
Презентация на тему Математический КВН 8 класс  Условия неопределенности выбора. Ограниченная рациональность
Условия неопределенности выбора. Ограниченная рациональность Векторы. Действия с векторами
Векторы. Действия с векторами Вычитание и сложение чисел
Вычитание и сложение чисел Нумерационные случаи сложения и вычитания чисел второго десятка
Нумерационные случаи сложения и вычитания чисел второго десятка Взаимное расположение графиков линейных функций. 7 класс
Взаимное расположение графиков линейных функций. 7 класс Обработка многократных измерений
Обработка многократных измерений Запомни координаты. Игра
Запомни координаты. Игра Теорема Пифагора для пятиклассников
Теорема Пифагора для пятиклассников Приложения производной
Приложения производной Порядок элемента. Теорема Лагранжа
Порядок элемента. Теорема Лагранжа Теорія множин. Відношення
Теорія множин. Відношення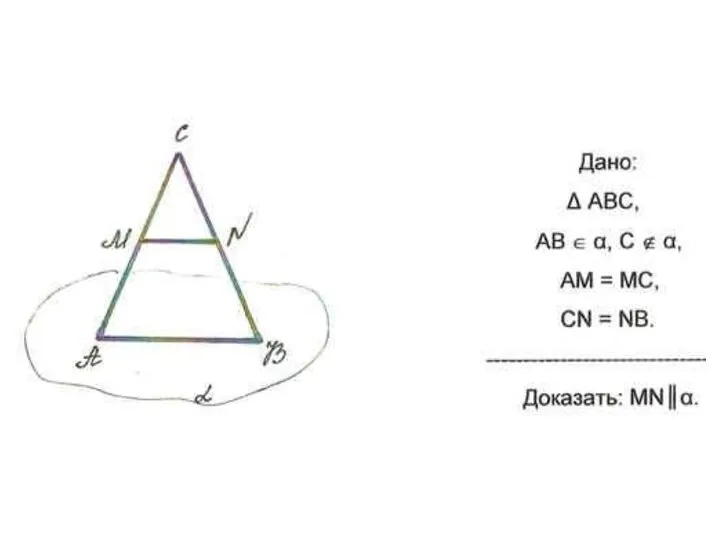 Параллельные прямые. Решение задач
Параллельные прямые. Решение задач урок 1 и 2 (1)
урок 1 и 2 (1) Обеспечивающие подсистемы АИС. Математическое обеспечение
Обеспечивающие подсистемы АИС. Математическое обеспечение Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Как можно заменить произведение равных сомножителей?
Как можно заменить произведение равных сомножителей? Многоранники
Многоранники