Содержание
- 3. Преподаватель: Кива М.Н. Интегрированный урок по теме «Применение производной при решении физических задач» 2019 г.
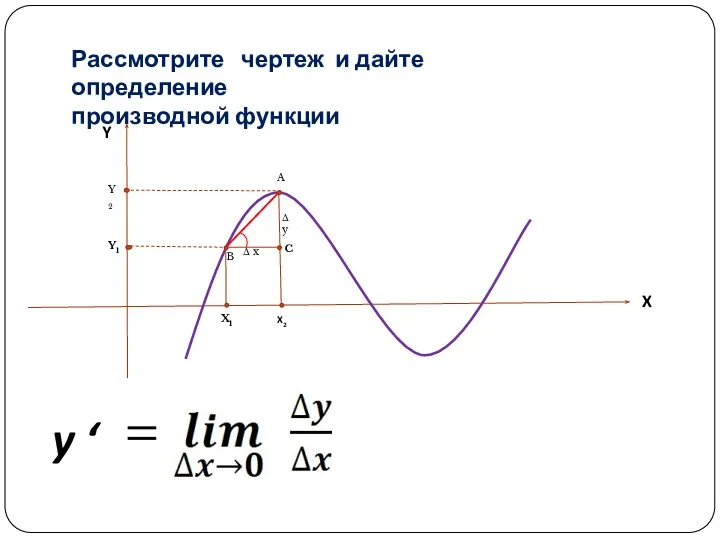
- 4. Δ x Δ y X1 X2 Y1 Y2 A C B X Y y ‘ Рассмотрите
- 5. Производная используется при решении следующих заданий: Вычислить производную Вычислить производную в заданной точке Все задания на
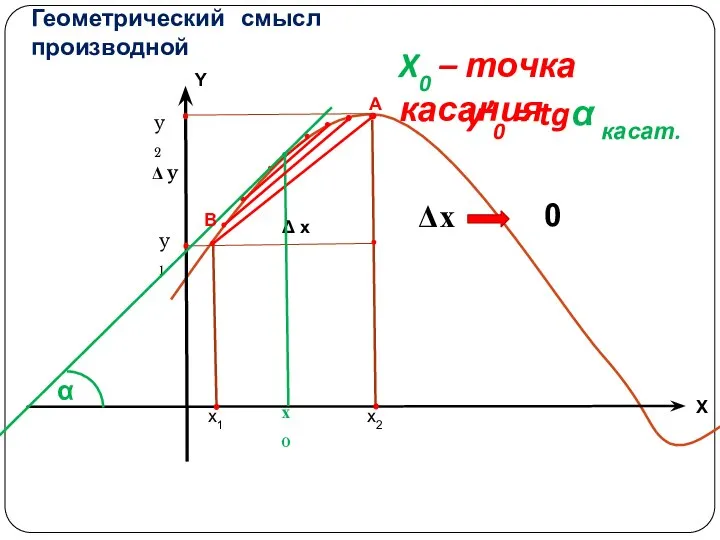
- 6. Геометрический смысл производной A Δх 0 х0 X0 – точка касания y’0 = tgα касат. α
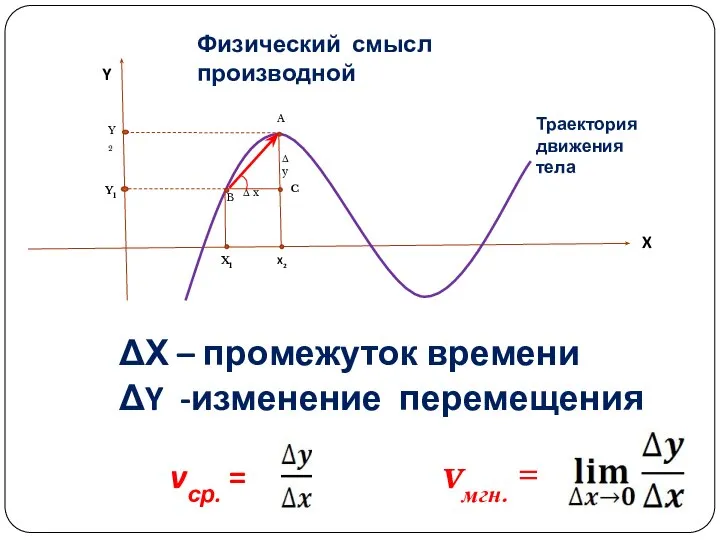
- 7. ΔХ – промежуток времени ΔY -изменение перемещения vср. = vмгн. = Δ x Δ y X1
- 8. Механический смысл второй производной Ускорение прямолинейного движения тела в данный момент равно второй производной пути по
- 9. v (t) = S′ (t) a(t) = V′ (t)
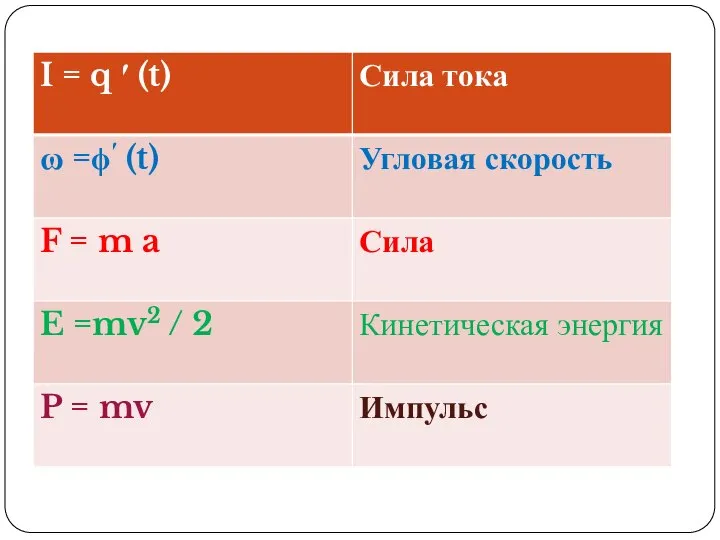
- 12. 1) Мощность есть производная работы по времени N = A ‘ (t) 2) Пусть дан неоднородный
- 13. Дано уравнение прямолинейного движения тела: S=3t2-5t+2, где S- путь, пройденный телом, м; t- время, с. Найдите
- 14. Точка движется по закону Найти скорость и ускорение через 4 с после начала движения (движение считать
- 15. Пусть q= 3t2 - 5t +8 - количество электричества, протекающее через поперечное сечение проводника за время
- 16. Пусть дан неоднородный стержень длины, масса неоднородного стержня меняется по закону: m=3x2 -5x +12. Найти линейную
- 17. Выбрать оптимальный объем производстваN фирмой, функция прибыли которой может быть смоделирована зависимостью: F(q) = q2 -
- 18. Прибыль фирмы задана зависимостью: F(q) = 5q2 - 5q + 12. Найти оптимальный объём производства N
- 19. Тело движется по закону x(t)=2t3 -2,5t2 + 3t +1. Найти скорость тела при t=1c. Тело движется
- 20. Самостоятельная работа Вариант 1. 1. Материальная точка движется по закону s(t)=12t+3t3. Найдите ее скорость и ускорение
- 21. Взаимопроверка Вариант 1. v(t)=s’(t)= 12+9t²; v(2)=12+36=48 (м/с); a(t)=v’(t)= 18t; a(2)=18·2= 36 (м/с²). 2. Ответ: 902,5 Дж.
- 22. ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ 1. (с)’ = 0 2. (un)’ =n∙un-1∙u’ 3. ( )’ = ∙u’ 4. (
- 24. Скачать презентацию



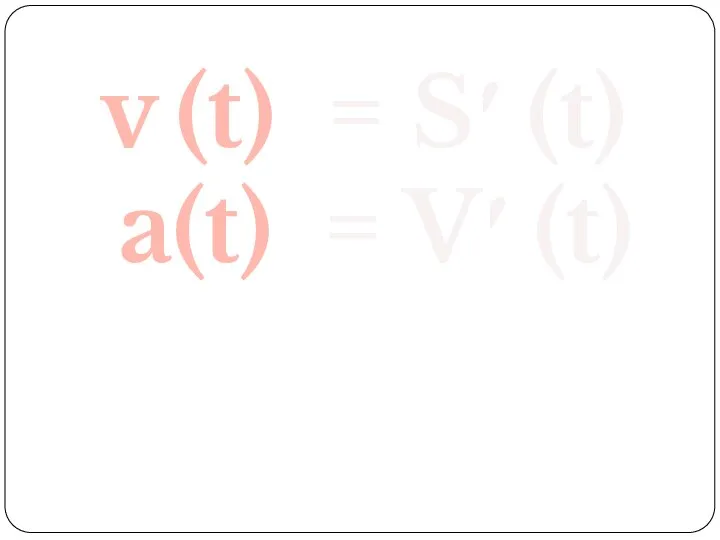












 Лекция 2
Лекция 2 Компланарны ли тройки векторов
Компланарны ли тройки векторов Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Простейшие задачи в координатах
Простейшие задачи в координатах Презентация на тему Шар (6 класс)
Презентация на тему Шар (6 класс)  Знаете ли вы... Высота, длина, вес
Знаете ли вы... Высота, длина, вес Фалес Милетский - один из первых геометров
Фалес Милетский - один из первых геометров Задачи математической статистики
Задачи математической статистики Оригами. Проект по математике
Оригами. Проект по математике Вырезаем квадрат
Вырезаем квадрат Измерение массы
Измерение массы Численное интегрирование
Численное интегрирование Математический диктант. Классная работа
Математический диктант. Классная работа Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Проекция группы геометрических тел
Проекция группы геометрических тел Презентация на тему Свойства функций и их графики
Презентация на тему Свойства функций и их графики  Проценты
Проценты Пифагор. Пифагорейская школа
Пифагор. Пифагорейская школа Нулевой угловой коэффицент
Нулевой угловой коэффицент Правильные многогранники
Правильные многогранники Своя игра 2
Своя игра 2 Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Основное свойство отрезка. Смежные и вертикальные углы
Основное свойство отрезка. Смежные и вертикальные углы Занимательные головоломки
Занимательные головоломки Проценты. Исследовательская работа
Проценты. Исследовательская работа Алгебра и начала математического анализа, 11 класс
Алгебра и начала математического анализа, 11 класс Презентация на тему Площадь круга и кругового сектора
Презентация на тему Площадь круга и кругового сектора  Решение тригонометрических уравнений
Решение тригонометрических уравнений