Содержание
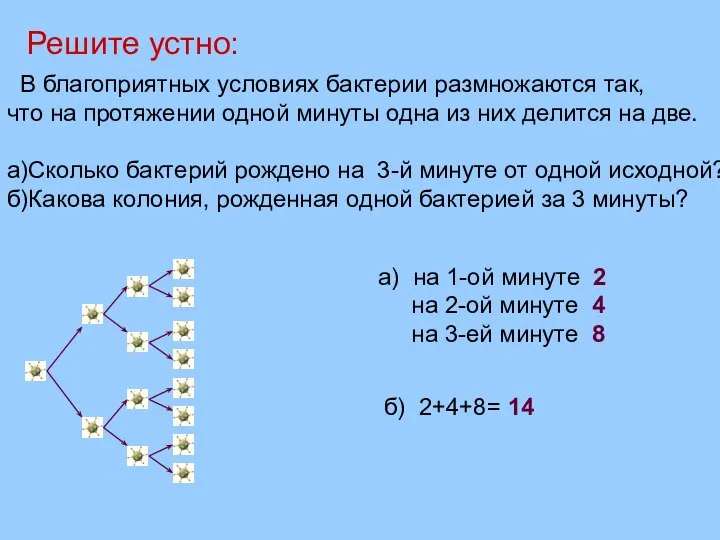
- 2. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на
- 3. Приходит как-то раз к одному богатому купцу мужик и предлагает сделку. «Давай, говорит, в течение месяца
- 4. План исследования Вычислить сумму, которую получит купец Узнать сумму, которую получит мужик Сравнить доходы Сделать выводы
- 5. Сумма, которую получит купец Sкупец= 100000руб х 30дней = =3000000руб
- 6. Сумма, которую получит мужик 1-ый день- 1коп 2-ой день- 2коп 3-ий день- 4коп 4-ый день- 8коп
- 7. Последовательность чисел 1; 2; 4; 8; 16;… представляет собой геометрическую прогрессию, у которой b1=1, q=2. Следовательно,
- 8. Выведем формулу для вычисления этой суммы Обозначим через Sn сумму n первых членов геометрической прогрессии. Sn=b1
- 9. Дано: геометрическая прогрессия b1=1 q=2 Найти: S30 Решение: Sn= S30= = 230 -1 = 1073741824 -1
- 10. Сравним доходы купец получил 3000000 руб мужик - 10737418 руб 23 коп разница составляет 7737418 РУБ
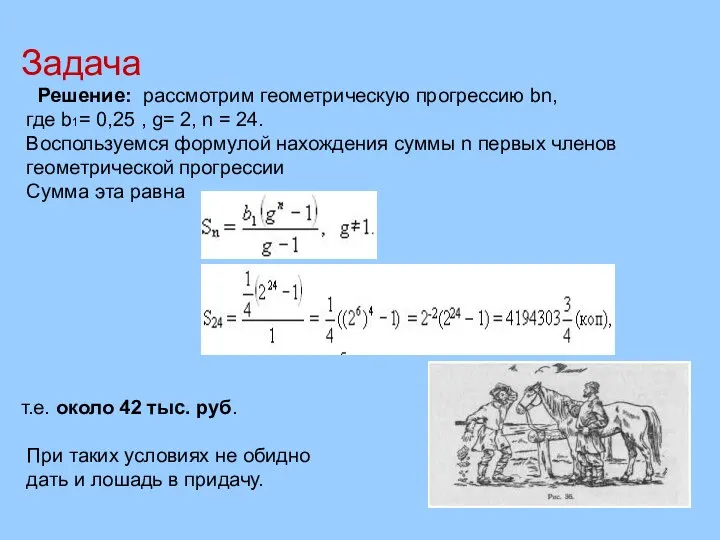
- 11. Решение: рассмотрим геометрическую прогрессию bn, где b1= 0,25 , g= 2, n = 24. Воспользуемся формулой
- 12. Sn = S5 = Дана геометрическая прогрессия b1=-4, q=2. Найти S5
- 13. Sn = b1=4, b2=16. Найти S6 S6 =
- 15. Скачать презентацию









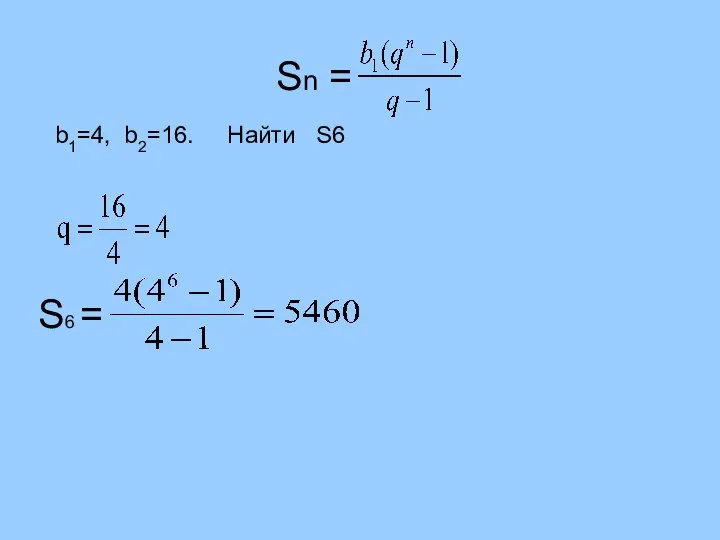
 калькуятор
калькуятор Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Ракеты и символы
Ракеты и символы Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Таблицы сложения и вычитания с числом 2
Таблицы сложения и вычитания с числом 2 Классификация функций
Классификация функций Вектор. Сложение векторов
Вектор. Сложение векторов Логические задачи. Математика и информатика. Тетрадь для 1–2 классов
Логические задачи. Математика и информатика. Тетрадь для 1–2 классов Математические основы ТАУ (продолжение)
Математические основы ТАУ (продолжение) Устный счет. 5 класс
Устный счет. 5 класс Числовые ряды
Числовые ряды Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка
Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка Если я знаю, что знаю мало, я добьюсь того, чтобы знать больше
Если я знаю, что знаю мало, я добьюсь того, чтобы знать больше Первообразная. Правила нахождения первообразных
Первообразная. Правила нахождения первообразных Комбинаторика. Из истории комбинаторики
Комбинаторика. Из истории комбинаторики Параллельность в пространстве
Параллельность в пространстве Задуманное число. Общий множитель
Задуманное число. Общий множитель Теорема Пифагора
Теорема Пифагора Анализ результатов ЕГЭ и ОГЭ 2021 по математике
Анализ результатов ЕГЭ и ОГЭ 2021 по математике Построение угла по транспортиру. Задача
Построение угла по транспортиру. Задача Сложение. Увеличиваем на 1
Сложение. Увеличиваем на 1 Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Геометричні переміщення
Геометричні переміщення Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20) Площадь прямоугольника
Площадь прямоугольника Надежность технических систем
Надежность технических систем Сечение поверхности плоскостью
Сечение поверхности плоскостью Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат
Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат