Пропорции. Проценты. Диаграммы

ПРОПОРЦИЯ

ЗАДАЧИ на пропорции (1)
Д/З/1 № 1003, 1004

РЕШЕНИЕ пропорций

РЕШЕНИЕ пропорций
Д/З/2 № 1013, 1014, 1006(в,г)

Производные ПРОПОРЦИИ
Если верна пропорция , то можно получить другие верные пропорции, которые называются производными.
В пропорции можно менять местами средние (крайние) члены
К обеим частям пропорции можно прибавлять (или вычитать) одно и то же число
или
Обе части пропорции можно умножать (или делить) на одно и то же число

РЕШЕНИЕ
производных пропорций
Решить пропорцию
По формуле при m=2 получим
Решите пропорции

Домашнее задание № 3 (Д/З/З)
Докажите, что если , то
Из пропорции получите производные пропорции по формулам

ПРЯМАЯ и ОБРАТНАЯ пропорциональность
Докажем, что в формуле А=ВС
При постоянном С величины А и В зависят прямо пропорционально
При постоянном В величины А и С зависят прямо пропорционально
При постоянном А величины В и С зависят обратно пропорционально

ПРЯМАЯ и ОБРАТНАЯ пропорциональность
Получили, что в формуле А=ВС
При постоянном С величины А и В зависят прямо пропорционально.
При постоянном В величины А и С зависят прямо пропорционально.
При постоянном А величины В и С зависят обратно пропорционально.
ПРЯМО ПРОПОРЦИОНАЛЬНО зависят произведение и один из множителей при постоянном значении другого множителя
ОБРАТНО ПРОПОРЦИОНАЛЬНО зависят множители при постоянном значении произведения
Путь и скорость; путь и время; работа и производительность; работа и время; стоимость и цена; стоимость и количество зависят ПРЯМО ПРОПОРЦИОНАЛЬНО.
Скорость и время, производительность и время, цена и количество зависят ОБРАТНО ПРОПОРЦИОНАЛЬНО.

ЗАДАЧИ на пропорциональность
(оформление)
Если при одинаковом времени даны S1 и v1, S2 и v2, которые зависят прямо пропорционально, то условие запишем в виде:
S1 v1 тогда верна
S2 v2 пропорция
Если при одинаковом пути даны t1 и v1, t2 и v2, которые зависят обратно пропорционально, то условие запишем в виде:
t1 v1 тогда верна
t2 v2 пропорция

ЗАДАЧИ на пропорциональность
(решение)

ЗАДАЧИ на пропорциональность
(решение)

ЗАДАЧИ на пропорциональность
(устное решение)
Д/З/4 1015, 1016, 1030(устно), 1031(устно)

ЗАДАЧИ на пропорциональность
(решение)

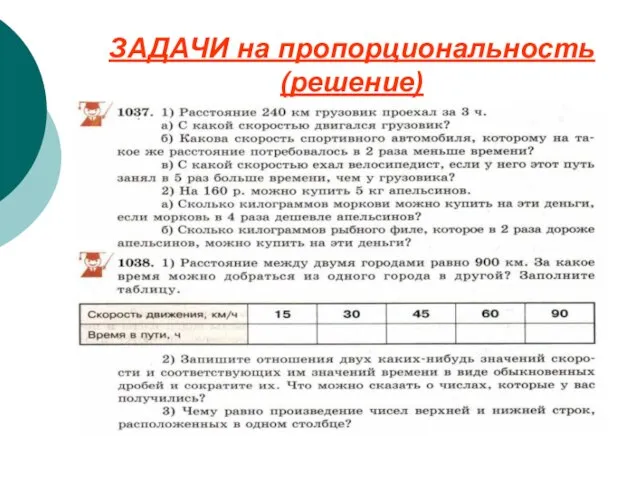
ЗАДАЧИ на пропорциональность
(решение)
Д/З/5 1054, 1055, 1056, 1057

ЗАДАЧИ на пропорциональность
(решение)
Д/З/6 1064, 1065, 1066

ЗАДАЧИ на пропорциональность
(решение)
Д/З/7 1073, 1074, 1075, 1076

ЗАДАЧИ на пропорциональность
(решение)
Д/З/8 1078, 1079, 1080

ПРОЦЕНТЫ

ПРОЦЕНТЫ и ДРОБИ
Сравним две известные формулы:
Формулировка «число а составляет часть от b» записывается на языке математики в виде равенства
(1)
Формулировка «число а составляет q% от b» записывается на языке математики в виде равенства

ЗАДАЧИ на ПРОЦЕНТЫ

ПРОЦЕНТЫ и пропорции
Из формулы 1. a, q – связаны прямо пропорционально,
2. a, b – связаны прямо пропорционально,
3. b, q – связаны обратно пропорционально,
4. b – принимают за 100%,
Значит, задачи на проценты можно решать с помощью пропорций.

ЗАДАЧИ на ПРОЦЕНТЫ
Д/З/9 1068, 1069, 1083

ЗАДАЧИ на ПРОЦЕНТЫ
Д/З/10 1017, 1018

ЗАДАЧИ на ПРОЦЕНТЫ
Д/З/10 Подготовка к контрольной работе