МиРИ Введение. Разд 1. Осн Метр ВЛ

Учебные пособия и метод. указания
1. Ленцман В.Л. Метрология и радиоизмерения. Учебное пособие – электронная версия. 2009 г.
2. Метрология и радиоизмерения.
Методические указания к лабораторным работам. СПб ГУТ. 2002г. (примеч. - 4 лаб.раб)
3. Методические указания по радиоизмерительным приборам /ЛЭИС. Л., 1986. Ч.1.
4. Методические указания по радиоизмерительным приборам /СПб ГУТ. 1996. Ч. 2.
5. Метрология и радиоизмерения. Под ред. В.И. Нефедова. Учебник для ВУЗов. М. «Высшая школа». 2006.
6. Любой другой учебник по Метрологии.

Введение в дисциплину
Термины
Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Единство измерений – состояние измерений, при котором:
их результаты выражены в допущенных к применению в РФ единицах величин, а
показатели точности измерений не выходят за установленные границы.
Примечание: В Российской Федерации применяется международная система единиц, рекомендованная Международной организацией законодательной метрологии (МОЗМ).

Метрология является научной и практической основой выполнения измерений,
а также процессов:
стандартизации,
сертификации и
обеспечения требуемого качества продукции и услуг.
Качество продукции или услуги характеризуют совокупностью определенных количественных параметров.
. Юридически строгие формулировки приведены в текстах федеральных законов
«Об обеспечении единства измерений»
(http://www.rsk-k.ru/zak.html) и
« О техническом регулировании» (http://www.consultant.ru/popular/techreg/).

Закон
«Об обеспечении единства измерений»
определяет сферу государственного регулирования обеспечения единства измерений, которая, в частности, распространяется на :
единицы величин,
эталоны единиц величин, а также на
измерения,
предусмотренные законодательством о техническом регулировании при выполнении работ по оценке соответствия продукции и услуг.

Федеральный закон
«О техническом регулировании»
регулирует отношения, возникающие :
при разработке, применении и исполнении обязательных требований к продукции, процессам проектирования, производства, эксплуатации, хранения, перевозки, реализации и утилизации,
при оценке соответствия.
Требования к функционированию единой сети связи РФ и использованию радиочастотного спектра устанавливаются и регулируются отдельным законодательством Российской Федерации в области связи

Техническое регулирование - правовое регулирование отношений в области установления, применения и исполнения: обязательных требований,
требований на добровольной основе
к продукции, процессам проектирования, производства, эксплуатации и оказанию услуг,
оценки и подтверждения соответствия.
.

Подтверждение соответствия - документальное удостоверение соответствия продукции или услуг требованиям:
технических регламентов,
положениям стандартов,
сводов правил
или
условиям договоров.

Технический регламент – документ, устанавливающий обязательные для применения и исполнения требования к объектам технического регулирования:
к продукции,
к процессам производства, строительства, монтажа, наладки, эксплуатации, хранения, перевозки, реализации и утилизации

Стандарт - документ, в котором в целях добровольного многократного использования устанавливают характеристики продукции, правила выполнения работ или оказания услуг.
Стандартизация – установление правил производства работ и характеристик продукции или услуг в целях их добровольного многократного использования.
Стандартизация обеспечивает упорядоченность в сферах производства и обращения продукции и повышение конкурентоспособности продукции, работ или услуг.

Сертификация – форма подтверждения соответствия продукции, производства работ, услуг (и т.п.) требованиям:
технических регламентов, положениям стандартов,
сводов правил или
условиям договоров.
Итогом такого подтверждения является выдача сертификата соответствия (документа) или знака.

1. Основы метрологии и теории погрешностей.
Термины и определения
Определения терминов метрологии даны по Федеральному закону
«Об обеспечении единства измерений»,
с использованием документа
Рекомендации по межгосударственной метрологии РМГ 29-99
Эти определения отличаются от использованных в учебниках прежних лет издания

1. Величина (физическая величина) – одно из свойств объекта, общее в качественном отношении для многих объектов, но в количественном отношении индивидуальное для каждого из них.
Примеры величин: длина, масса, время, электрический ток, напряжение и т.п.
Примечание:
В федеральном законе 2008 г «Об обеспечении единства измерений» прилагательное «физическая» во всех определениях опущено. Поэтому в дальнейшем будет использован термин «величина».

2. Единица величины (ЕВ) – фиксированное значение величины, которое принято за единицу данной величины и применяется для количественного выражения однородных с ней величин.
Определение РМГ 29-99 проще:
Единица величины - величина фиксированного размера, которой условно присвоено числовое значение, равное 1.

Примечания:
Единица величины обычно определена свойствами реального объекта - эталона.
Часто используемое в технической литературе выражения типа
«величина массы»
или
«величина напряжения»
являются неправильными, поскольку масса и напряжение – это и есть величины

3. Измерение – совокупность операций, выполняемых для определения количественного значения величины.
Определение этого термина в РМГ 29-99 более информативно:
Измерение - совокупность операций по применению технического средства, хранящего единицу величины, обеспечивающих нахождение соотношения измеряемой величины с ее единицей и получение значения этой величины.

Совокупность используемых единиц величин образует систему, в которой одни величины приняты за независимые, а другие определены как функции независимых величин.
В настоящее время практически все страны мира используют единую международную систему единиц величин СИ
SI – System International
В ней семь основных единиц, условно принятых за независимые
На их основе образованы с использованием соответствующих уравнений производные единицы.
Многие из производных единиц величин имеют специальные наименования: вольт (В), герц (Гц), ватт (Вт) и т.д.

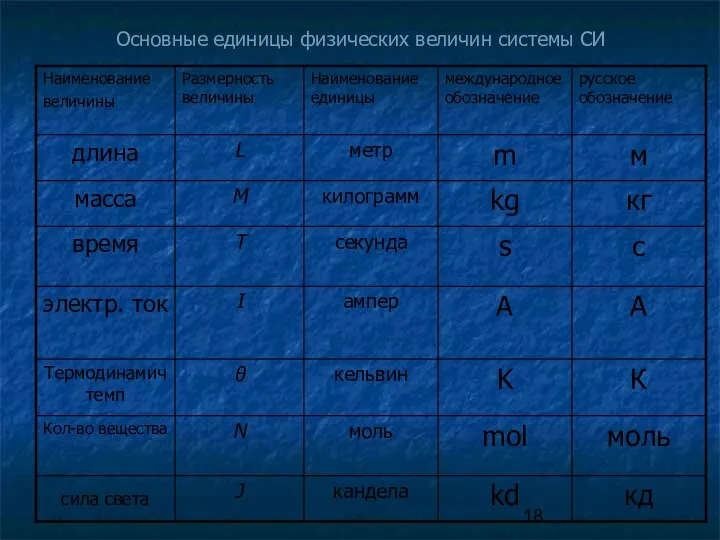
Основные единицы физических величин системы СИ

Определения некоторых основных единиц

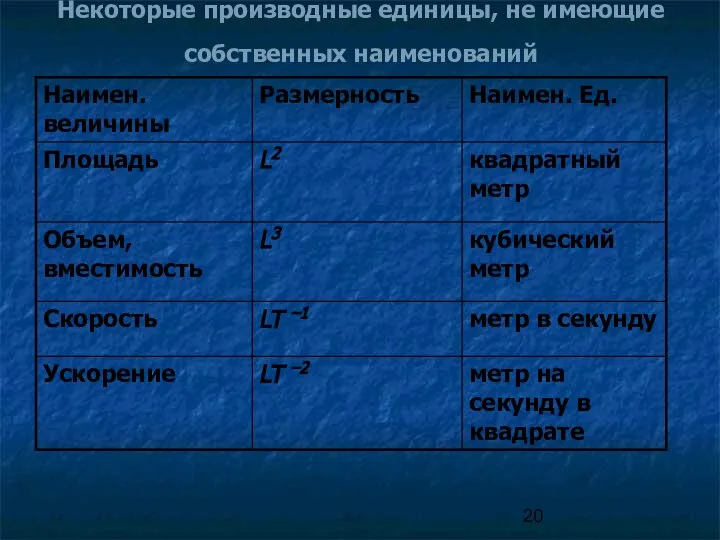
Некоторые производные единицы, не имеющие собственных наименований

4. Средство измерений - техническое средство, предназначенное для измерений.
Определение РМГ 29- 99 уточняет:
Средство измерений
имеет нормированные метрологические характеристики,
воспроизводит единицу физической величины,
обеспечивает неизменность размера этой единицы в пределах установленной погрешности в течение известного интервала времени.
Перечисленные факторы и «делают» техническое средство средством измерений.

Поверка средств измерений - совокупность операций, выполняемых в целях подтверждения соответствия средств измерений метрологическим требованиям.
Калибровка средств измерений - совокупность операций, выполняемых в целях определения действительных значений метрологических характеристик средств измерений.
Для средств измерений, относящихся к сфере государственного регулирования обеспечения единства измерений, регламентированы процедуры, обеспечивающие:
утверждение типа средств измерений;
поверку средств измерений, в том числе первичных и вторичных эталонов;
лицензирование деятельности юридических и физических лиц на право изготовления, продажи и ремонта средств измерений.

5. Методика (метод) измерений - совокупность конкретно описанных операций, выполнение которых обеспечивает получение результатов измерений с установленными показателями точности.
Это определение Федерального закона ОЕИ
не делает различия между терминами «методика» и «метод», что соответствует международному толкованию этих терминов

Ранее в документах и учебниках метод измерения рассматривался как совокупность приемов сравнения измеряемой величины с ее единицей.
Наиболее известны были два метода:
метод непосредственной оценки
и
метод сравнения,
упоминание о которых еще долго будет встречаться в литературе

6. Результат измерения (РИ)– значение величины, полученное путем ее измерения.
Примечание: фактически РИ - это произведение некоторого числа на единицу величины:
Х = n [х], где :
Х - результат, n - число, [х] – единица величины.
Это соотношение называют уравнением измерений. Например, U=2,35В, Т= 5,64 мс, f = 12,345 МГц. Результат измерения должен обязательно сопровождаться указанием условного обозначения единицы величины.

7. Погрешность измерения - отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Примечание: Истинное значение величины принципиально найти нельзя - это некоторая абстракция. На практике при определении погрешности вместо истинного значения используют так называемое действительное значение.
Действительное значение – значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Примечание: не следует путать этот термин с термином «действующее значение» (например, напряжения).

1.2. Классификация измерений
По способам обработки результатов измерения подразделяют на 4 вида:
прямые измерения,
косвенные,
совместные,
совокупные.
Прямое измерение – измерение, при котором искомое значение величины получают непосредственно от средства измерений.
Например, получение результата измерения напряжения с помощью вольтметра не требует какой-либо обработки.

Косвенное измерение – определение искомого значения величины на основании результатов прямых измерений других величин, функционально связанных с искомой величиной.
Например, измерение сопротивления резистора с использованием закона Ома:
R= U/I
на основе результатов измерения напряжения и тока требует расчета, как самого значения сопротивления, так и погрешности его определения ΔR, которая будет зависеть от погрешностей прямых измерений напряжения ΔU и тока ΔI. Далее будут рассмотрены процедуры такой обработки.

Совместные измерения - проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними.
Такие измерения позволяют найти зависимость одной величины от другой (или от нескольких других), например, построить вольтамперную характеристику нелинейного элемента.
При построении по совокупности полученных точек итоговой зависимости, удовлетворяющей некоторой модели, используют специальные математические методы обработки результатов, в частности, «метод наименьших квадратов». При этом итоговая кривая может не проходить через экспериментально полученные точки

Совокупные измерения - проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
Простейшим примером таких измерений является определение сопротивлений R1 и R2 двух резисторов путем двух измерений сопротивления при их последовательном и параллельном соединении.
Определив: Rпосл. = R1+ R2 и
Rпар. = ( R1∙ R2)/(R1+ R2),
можно найти значения R1 и R2.

1.3. Классификация погрешностей измерений
По форме записи погрешности принято разделять на:
абсолютные,
относительные,
приведенные.
Абсолютная погрешность – погрешность, выраженная в единицах измеряемой величины (т.е. она имеет размерность). За условным обозначением абсолютной погрешности в метрологии зарезервирована заглавная греческая буква «дельта»:
Δ= Аx - Аист.
Поскольку истинное значение Аист найти невозможно, на практике погрешность результата измерения Аx определяют приближенно с использованием действительного значения:
Δ= Аx - Адейств..
При записи значения абсолютной погрешности обязательно следует указывать единицу величины.

Относительная погрешность (условное обозначение – строчная греческая буква δ – «дельта») используется в двух формах записи:
δ = Δ/ Аx - безразмерная форма записи,
δ = (Δ/ Аx ) 100%- в процентах.
В англоязычных документах относительные погрешности часто указывают в миллионных долях от измеряемой величины (в промилях):
1 ppm (part per million) = 10-6.

Не следует путать строчную греческую букву
δ – «дельта»
со строчной греческой буквой
σ – «сигма»,
которая зарезервирована в метрологии за условным обозначением
среднего квадратического отклонения (СКО)
случайной погрешности

Приведенная погрешность – отношение абсолютной погрешности средства измерений к условно принятому (нормирующему) значению величины, постоянному во всем диапазоне измерений или в части диапазона.
За нормирующее значение Анорм. обычно принимают диапазон (поддиапазон) или верхний предел средства измерения. Приведенную погрешность обычно выражают в процентах:
δпр = (Δ/ Анорм ) 100%.
Приведенная погрешность, как правило, остается постоянной при выборе другого поддиапазона средства измерения

По характеру изменения при повторных измерениях
погрешности подразделяют на:
систематические;
случайные;
грубые.
Систематическая погрешность – составляющая погрешности результата измерения, которая остается постоянной по значению и знаку при повторных измерениях одной и той же величины.
К систематическим погрешностям принято относить и погрешности, которые изменяются при повторных измерениях по какому-либо детерминированному закону.

Систематическую погрешность бывает трудно обнаружить и определить – для этого надо иметь оценку действительного значения измеряемой величины. Но если значение и знак систематической погрешности найдены, ее можно исключить из результата измерения - ввести поправку.
Как правило, полностью исключить систематическую погрешность, нельзя. Остается так называемая «неисключенная» систематическая погрешность (НСП), определяемая, в итоге, некоторым интервалом ±Δ, поскольку информация о знаке «потеряна» или просто не учитывается.

НСП – это составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Для анализа НСП часто применяют методы теории случайных величин. Поэтому в литературе можно встретить такое, на первый взгляд странное выражение, как «закон распределения неисключенной систематической погрешности». Кроме того, слово «неисключенная» часто опускают.

Случайная погрешность – составляющая погрешности результата измерения погрешность, которая изменяется случайным образом (по знаку и значению) при повторном измерении одной и той же величины.
В качестве модели случайной погрешности берется случайная величина в математическом смысле этого термина.

Наличие случайной погрешности обычно легко обнаруживается при повторных измерениях одной и той же величины (разумеется, мы должны быть уверены, что сама измеряемая величина при этом не изменяется).
Исключить случайную погрешность принципиально невозможно. Но, зная закон распределения этой погрешности, можно приближенно оценить, в каком интервале и с какой вероятностью она будет находиться при многократном повторении таких измерений. Кроме того, случайную погрешность можно уменьшить путем статистического усреднения повторных независимых измерений !

Грубая погрешность – погрешность, существенно превышающая ожидаемую в данных условиях. Грубую погрешность, обусловленную неправильными действиями оператора, называют промахом.
Рассмотрим пример одновременного проявления всех трех видов погрешностей при измерении постоянного напряжения 1,0000 В, известного с высокой точностью – следовательно его можно принять за действительное значение напряжения
U действ.
Результаты измерений получились такими:

Результаты измерения напряжения, имеющие все три составляющие погрешности: случайную, систематическую и грубую
Естественно предположить, что компактный разброс результатов измерений вблизи значения 1,0000В обусловлен наличием случайной погрешности, а результат 1,35 В, по-видимому, связан с появлением грубой погрешности.

Грубую погрешность можно устранить одним из следующих способов:
просто на основе интуиции «отбросить» результат 1,35 В (это, разумеется, надо делать очень осторожно, чтобы не потерять редко появляющиеся, но очень важные данные);
обнаружить причину появления грубой погрешности (например, сбои в напряжении питания), устранить ее и провести измерения заново, обеспечив постоянство условий проведения повторных измерений;
использовать специальные математические процедуры «отбраковки» грубых погрешностей.

Устранив грубую погрешность, можно :
найти среднее значение результата измерения напряжения,
оценить систематическую погрешность как отклонение среднего значения от действительного,
оценить статистические характеристики случайной составляющей погрешности (подробнее об этом далее).

По зависимости от измеряемой величины погрешности принято подразделять на:
аддитивные;
мультипликативные.
Аддитивная – погрешность, значение которой не зависят от измеряемой величины. Аддитивный характер могут иметь как систематические, так и случайные погрешности.
Мультипликативная – погрешность, значение которой изменяется в зависимости от измеряемой величины.
Как правило, мультипликативные погрешности растут с увеличением измеряемой величины.

По причинам возникновения погрешности подразделяются на:
Инструментальные и
методические.
Инструментальная погрешность – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений (обусловлена его «неидеальностью»).
Методическая погрешность (погрешность метода измерения)- составляющая погрешности измерений, обусловленная несовершенством принятого метода измерений.
Как правило (но не всегда), методические погрешности имеют систематический характер и очень редко - случайный.

К методическим принято относить погрешности, обусловленные неполнотой наших представлений об измеряемом объекте (т.е. несоответствие используемой модели реальному объекту).
Например, измерить действующее значение напряжения синусоидальной формы можно очень просто, измерив его амплитуду и разделив полученный результат на √2.
Но если измеряемый сигнал отличен по форме от синусоиды (а мы не догадываемся, что в нем присутствуют вторая, третья и т.д. гармоники), то такое измерение будет иметь существенную методическую погрешность.

По условиям применения средств измерения погрешности подразделяют на:
основные и
дополнительные.
Основная – погрешность средств измерения в так называемых нормальных условиях измерения.
Нормальные условия – условия, записанные в технической документации как нормальные
Дополнительная – погрешность, которая возникает при отклонении условий работы средства измерения от нормальных - в так называемых рабочих условиях.

1.4. Оценка погрешностей и правила представления результатов измерения
Определение термина «единство измерений» требует указания вместе с результатом показателей точности - погрешностей измерения.
На практике используют два подхода к оценке погрешностей:
по нормируемым метрологическим характеристикам используемых средств измерений.
экспериментальный.

Экспериментальная оценка погрешностей
1. Проводят ряд измерений действительного значения в неизменных условиях.
2. Исключают грубые погрешности.
3. Определяют значение и знак систематической составляющей погрешности и исключают ее из результата - вводят поправку.
4.Полностью исключить систематическую погрешность, как правило, нельзя, а иногда просто нецелесообразно. Остается так называемая неисключенная систематическая погрешность (нсп), знак которой уже неизвестен, а ее значение оценивают обычно симметричным интервалом ±Δнсп.
5. Оценивают пределы случайной погрешности, обычно в форме симметричного доверительного интервала при заданной доверительной вероятности
Определение этих понятий и необходимые формулы рассмотрим позже.

5. Если случайная погрешность заметно больше неисключенной систематической погрешности, то именно случайная составляющая погрешности будет определять итоговую погрешность результата измерения. Например:
U ± Δдов , Рдов = 0,9
6. Если случайная погрешность заметно меньше неисключенной систематической погрешности, то именно неисключенная систематическая погрешность будет определять погрешность результата:
U ± ΔНСП
7. В некоторых случаях приходится находить суммарную (результирующую) погрешность, складывая по определенным формулам полученные оценки случайных и неисключенных систематических погрешностей.

При окончательном представлении результат измерения необходимо записать в следующем виде:
U ± Δдов , Рдов = (например 0,9)
где – Рдов -доверительная вероятность, которой соответствует погрешность измерения Δдов .
Если погрешность оценена не вероятностным способом, например, по нормируемым метрологическим характеристикам средств измерения, то соответствующую доверительную вероятность указать невозможно и ее, разумеется, не указывают.

При таком представлении надо соблюдать два правила:
1) При окончательной записи значения погрешности, задаваемой некоторым интервалом, следует использовать не более двух значащих цифр.
Можно использовать и одну значащую цифру, если это не приведет к большой погрешности округления. Как правило, одну значащую цифру оставляют, если цифра старшего разряда погрешности равна 3 и больше.
2) Наименьшие разряды результата измерения и округленного значения погрешности должны быть одинаковы.

Значащие цифры числа – это все цифры от первой слева, не равной нулю, до последней записанной цифры справа. При этом нули, следующие из множителя 10n , не учитываются.
Например, в числах 12; 1,2; 0,12; 0,00012; 1,2 ∙10-10 – всего две значащие цифры! А в числе 120 – их три!
Примечание: иногда используемое выражение
«значащие цифры после запятой»
здесь не применимо. Такое толкование термина «значащие цифры» при округлении погрешностей приводит к ошибкам!

Рассмотрим пример
Получены (например, расчетным путем при статистической обработке) результат измерения напряжения
Uх=1,234567 В и погрешность Δ= ± 0,0234567 В при доверительной вероятности Рдов=0,9.
Сначала в соответствии с первым правилом округляем полученное значение погрешности:
Δ = ± 0,0234567 В =~ ± 0,023 В.
В этом числе две значащие цифры. Это значение погрешности можно было бы записать и так
± 23 мВ.
Здесь тоже две значащие цифры, хотя десятичная запятая вообще отсутствует.
Обратите внимание, что при использовании дольных единиц напряжения мкВ такую погрешность грамотно записать нельзя! Это слишком малая единица для такого значения погрешности!

Теперь в соответствии со вторым правилом округляем результат, оставляя в нем последней цифру того разряда, на котором оканчивается округленное значение погрешности, и окончательно записываем:
Uх = (1,235 ±0,023) В, Рдов=0,9 или
Uх = (1235 ± 23) мВ, Рдов=0,9.
Обратите внимание, что такая форма записи со знаком ± , фактически эквивалентна использованию неравенства:
(1,212 В ≤ Uист ≤ 1,258 В) при Рдов=0,9,
но более компактна и наглядна.
Если исходное расчетное значение погрешности было бы ± 0,05432В (цифра старшего разряда погрешности больше, чем 3), то окончательное значение погрешности следовало бы округлить до одной значащей цифры:
± 0,05 В,
а результат измерения следовало записать так:
Uх = (1,23 ± 0,05) В, Рдов=0,9.

Рассмотренные правила обоснованы следующими соображениями:
теоретически можно поставить вопрос о «погрешности определения значения погрешности», и показать, что оценки погрешностей, в принципе, находятся довольно приближенно. Поэтому при их окончательной записи достаточно использовать одну - две значащие цифры;
простой здравый смысл позволяет утверждать, что если к любому интервалу, определяющему погрешность результата, добавить или отнять его малую часть, то значение погрешности практически не изменится.

1. 5. Виды средств измерений
Средства измерений (СИ) принято подразделять на:
меры;
измерительные приборы;
измерительные преобразователи;
измерительные установки;
измерительные системы.

Мера – средство измерений, предназначенное для воспроизведения и (или) хранения величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью.
Измерительный прибор – СИ, предназначенное для получения значений измеряемой величины в установленном диапазоне.
Измерительный преобразователь – средство с нормативными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или передачи. ИП или входит в состав какого-либо измерительного прибора (измерительной установки, измерительной системы и др.), или применяется вместе с каким-либо средством измерений.

Измерительная установка – совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей и других устройств, предназначенная для измерений одной или нескольких величин и расположенная в одном месте.
Измерительная система – совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей, ЭВМ и других технических средств, размещенных в разных точках контролируемого объекта и т.п. с целью измерений одной или нескольких величин, свойственных этому объекту, и выработки измерительных сигналов в разных целях.

1.6. Нормируемые метрологические характеристики СИ
Метрологические характеристики (МХ) – это характеристики (свойства) СИ, от которых зависит результат и погрешность измерения. Напомним, что наличие метрологических характеристик определяет само понятие «средства измерения».
Несмотря на специфику нормирования свойств различных СИ, можно сформулировать некоторый общий перечень МХ, который фирмы-изготовители обязательно указывают в технической документации:
1. Диапазон измерения (часто этот диапазон разбивают на поддиапазоны);

2. Разрешающая способность, которую задают несколькими различными способами:
2.1. ценой деления шкалы - для аналоговых приборов.
Важно иметь ввиду, что цена деления шкалы – это не погрешность СИ. Обычно при отсчете показаний аналогового прибора последнюю значащую цифру результата получают путем интерполяции положения «стрелки» в пределах одного деления шкалы;
2.2. ценой единицы младшего разряда - для цифровых СИ.
Эта характеристика зависит от установленного поддиапазона измерения;
2.3. количеством (k) десятичных разрядов цифрового отсчетного устройства- для цифровых СИ.
2.4. количеством (n) двоичных разрядов кода, (например, «АЦП на 10 двоичных разрядов» т.е. n=10),
По значениям k или n можно определить количество уровней квантования измеряемой величины:
N=2 n = 10 k

В технических описаниях СИ зарубежных фирм часто используют несколько жаргонный термин, например,:
«вольтметр на 4,5 десятичных разряда».
Это означает, что ЦОУ имеет 5 разрядов, но старший разряд – неполный, в нем могут отображаться
не все цифры от 0 до 9, а, например,
только цифры 0 или 1, или
только цифры от 0 до 4

3. Погрешность СИ задают предельно допускаемым значением (интервалом со знаком ±) в виде числа или выражения в форме:
3.1. абсолютной погрешности (достаточно редко):
∆=±a – если абсолютная погрешность имеет чисто аддитивный характер,
∆=±b∙Ax - если абсолютная погрешность имеет чисто мультипликативный характер (Ax- результат измерения),
∆=±(a+b Ax) - если абсолютная погрешность имеет и аддитивную и мультипликативную составляющие,

3.2. относительной погрешности:
δ=±b,
δ=±(b+a/Ax ), или
δ=±{c+d[(Uk /Ux )-1])} %
эта последняя формула, где Uk – диапазон измерения, а Ux - результат измерения, широко использовалась ранее при нормировании погрешностей отечественных цифровых вольтметров;
3.3. приведенной погрешности:
δпр = ±γ % (как правило, в %)

Некоторые зарубежные фирмы нормируют погрешности средств измерений как сумму двух составляющих в такой форме:
± (% of reading + % of range ), т.е.
± (% от показаний + % от поддиапазона).
Например, фирма Agilent для своего 6,5 разрядного вольтметра на поддиапазоне измерения 1,0 В нормирует погрешность так:
± (0,0030% от показаний + 0,0007% от диапазона).
В документации вольтметра представлена целая таблица таких формул для разных поддиапазонов и условий применения.

4. Условия применения (температура, давление, влажность, допустимые пределы изменения напряжения питающей сети, интервал времени от момента поверки или калибровки прибора, другие влияющие параметры.) Условия применения иногда подразделяют на:
нормальные условия, для которых нормируют основную погрешность,
рабочие условия (более широкие, чем нормальные), для которых нормируют дополнительную погрешность (или допускаемое изменение показаний).
5. Быстродействие - количество измерения в секунду (для цифровых СИ) или
Время установления показаний (для аналоговых СИ).
Чем выше быстродействие СИ, тем, как правило, больше нормируемая погрешность.

6. Входной импеданс - полное входное сопротивление
Эквивалентная схема входной цепи СИ, как правило, может быть представлена в виде параллельного соединения резистора и конденсатора:
Нормирование параметров R вх и С вх позволяет пользователю оценить влияние подключения СИ на измеряемую цепь - оценить и ввести поправку на соответствующую погрешность, если она носит систематический характер. Разумеется, при этом надо знать выходное сопротивление источника измеряемого сигнала.

Классы точности средств измерений
Для многих средств измерений очень давно было введено понятие класса точности.
Для различных СИ классы точности могут задаваться различным образом.
Цифры, указывающие КТ, выбирают из определенного набора (напр. 0,5; 1,5; 2,5; 4)
Класс точности - обобщенная характеристика точности СИ, задаваемая пределами допускаемой основной приведенной или
относительной погрешности.
Рассмотрим несколько простейших способов задания класса точности электроизмерительных приборов:

Первый способ задания класса точности
1. Цифра, обозначенная на шкале и указывающая класс точности, не сопровождается какими-либо другими значками (из перечисленных далее), например,
2.5. Это условное обозначение нормируемой приведенной погрешности ±2,5%, по которой можно, не пользуясь техническим описанием, сразу определить предельно допускаемую абсолютную погрешность на выбранном поддиапазоне:
Δ = ±( δ пр /100% ) А норм

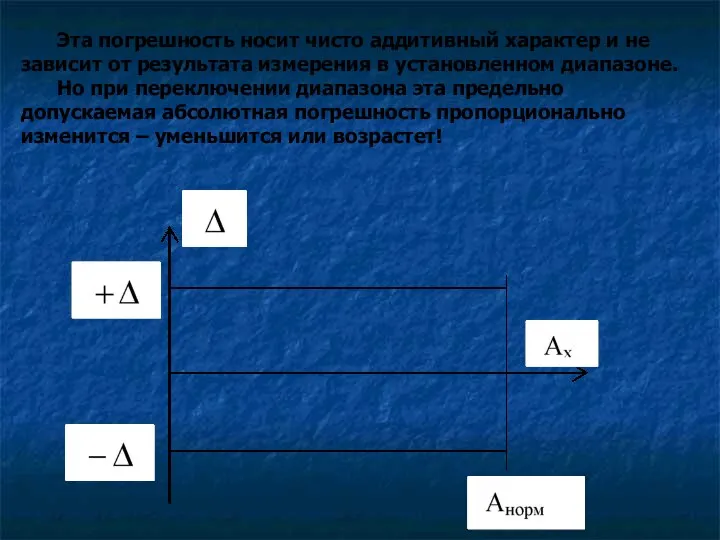
Эта погрешность носит чисто аддитивный характер и не зависит от результата измерения в установленном диапазоне.
Но при переключении диапазона эта предельно допускаемая абсолютная погрешность пропорционально изменится – уменьшится или возрастет!

Второй способ задания класса точности
2. Цифра, обозначающая класс точности, обводится кружком:
(1,5)
В данном случае класс точности определяет нормируемую предельно допускаемую относительную погрешность ±1,5%.
Предельно допускаемую абсолютную погрешность нетрудно сосчитать:
Δ = ±(/ δ /100% )АХ

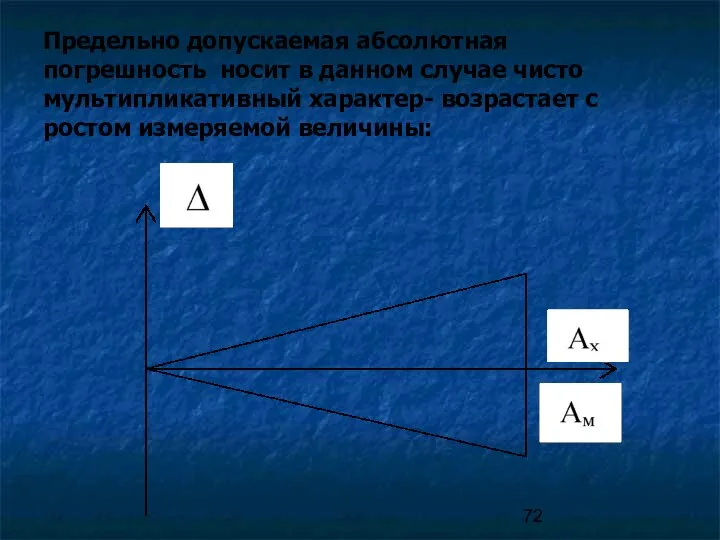
Предельно допускаемая абсолютная погрешность носит в данном случае чисто мультипликативный характер- возрастает с ростом измеряемой величины:

Третий способ задания класса точности
3. Для цифровых вольтметров класс точности было принято задавать двумя цифрами, разделенными косой чертой, например:
0.25/0.15
В данном случае цифры класса точности определяют коэффициенты c и d в двучленной формуле для предельно допускаемой относительной погрешности:
δ=±(c+d[(U k /U x )-1]) % ,
где Uk – диапазон измерения, Ux - результат измерения,
c и d – коэффициенты, например:
c = 0.25%, d = 0.15 %.

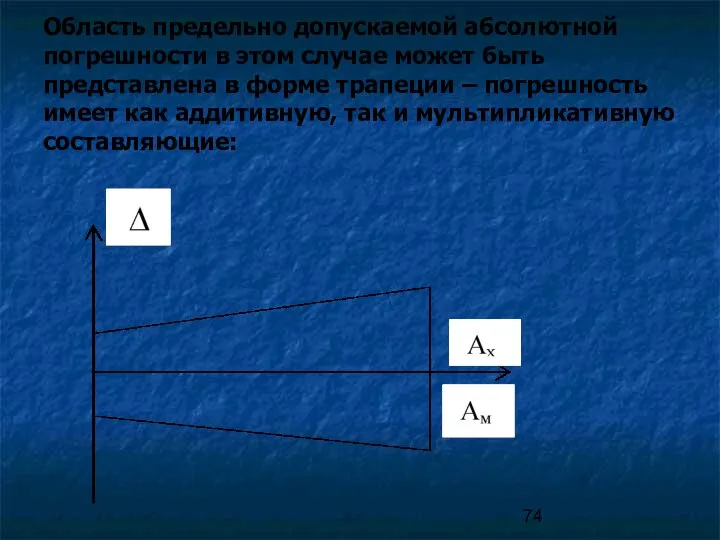
Область предельно допускаемой абсолютной погрешности в этом случае может быть представлена в форме трапеции – погрешность имеет как аддитивную, так и мультипликативную составляющие:

Четвертый способ задания класса точности
Цифра, обозначающая класс точности, сопровождается указанием скобки снизу от цифры, например:
4 Такой способ задания класса точности раньше использовали для аналоговых приборов с существенно нелинейной шкалой (например, для омметров). Цифра 4 указывает приведенную погрешность в процентах от максимальной длины шкалы в миллиметрах:
δпр = ± [Δ L(мм)/ Δ Lмах(мм)]100%

Зная длину шкалы прибора, можно определить абсолютную погрешность в миллиметрах, «мысленно» наложить этот отрезок на нелинейную шкалу омметра в месте расположения указателя («стрелки») и приближенно оценить абсолютную погрешность в единицах сопротивления. Поскольку шкала омметра нелинейная, то в начале шкалы погрешность измерения сопротивления таким оммеромможет составлять, например, ±0,5 кОм, а конце - ±15 кОм.
В настоящее время понятие класса точности для многих средств измерений постепенно выходит из употребления

1.7. Случайные погрешности
В качестве модели случайной погрешности в метрологии принимается случайная величина – величина, знак и значение которой принципиально нельзя предсказать исходя из условий проведения испытаний.
Случайная величина полностью характеризуется законом распределения, который дает информацию об области значений случайной величины и
о вероятности, с которой эта случайная величина принимает то или иное значение.
Полезно напомнить, что если мы знаем закон распределения случайной погрешности, то мы знаем о ней буквально все, что можно о ней знать.

В метрологии законы распределения принято задавать в дифференциальной форме – в виде функции или графика плотности вероятности, причем условие нормировки этой функции принято таким:

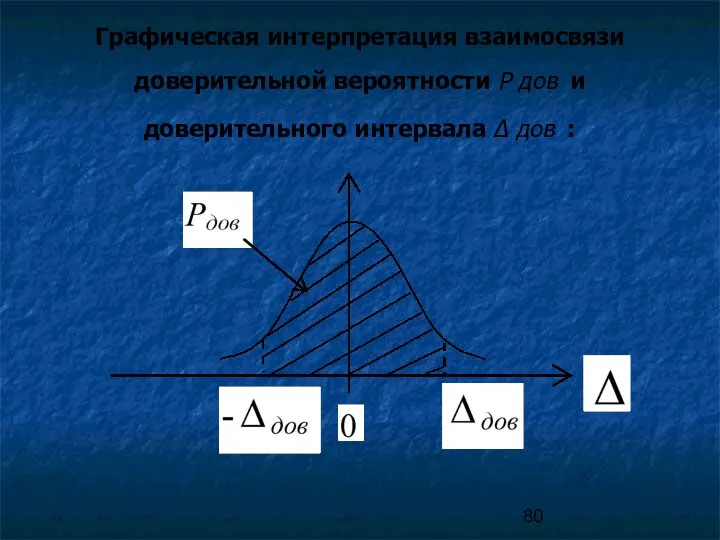
Уравнение
определяет взаимосвязь понятий
доверительного интервала Δ дов и доверительной вероятности Р дов
С вероятностью Pдов случайная погрешность будет находиться в пределах доверительного интервала
от – Δ дов до +Δ дов.

Графическая интерпретация взаимосвязи доверительной вероятности Р дов и доверительного интервала Δ дов :

При решении измерительных задач довольно часто приходится иметь дело с так называемым нормальным законом распределения случайных погрешностей (распределением Гаусса).
Некоторым теоретическим обоснованием этого факта служит центральная предельная теорема Ляпунова, который доказал, что при некоторых предположениях распределение суммы случайных величин с произвольными законами распределения близко к нормальному.

В таком виде распределение зависит только от параметра σ («сигма») - среднего квадратического отклонения (СКО).
Напомним, что СКО - это положительное значение квадратного корня из дисперсии.
Среднее значение погрешности (мат. ожидание) в данном случае принято равным нулю – т.е. предполагаем, что систематическая погрешность отсутствует.

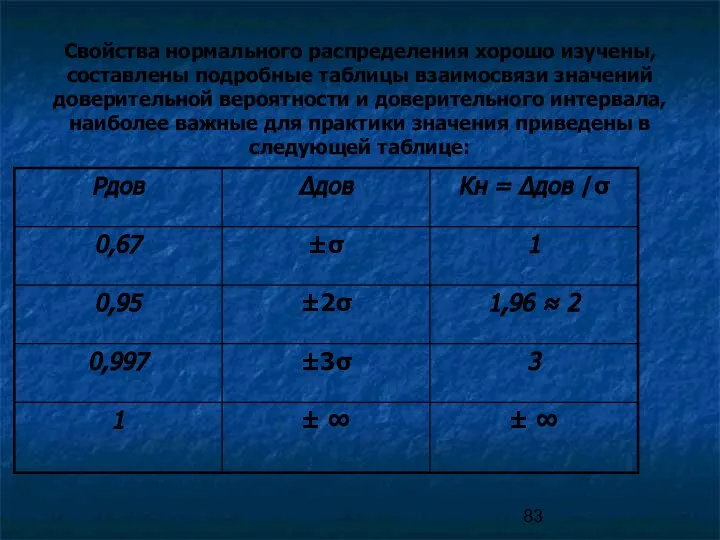
Свойства нормального распределения хорошо изучены, составлены подробные таблицы взаимосвязи значений доверительной вероятности и доверительного интервала, наиболее важные для практики значения приведены в следующей таблице:

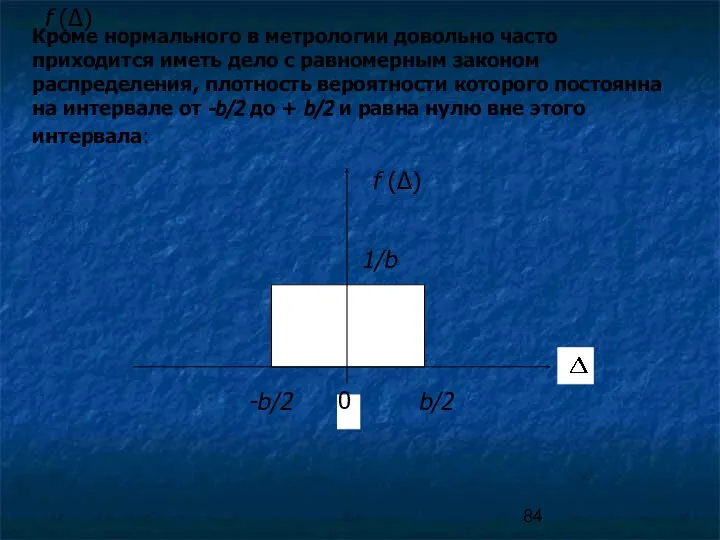
f (Δ)
f (Δ)
Кроме нормального в метрологии довольно часто приходится иметь дело с равномерным законом распределения, плотность вероятности которого постоянна на интервале от -b/2 до + b/2 и равна нулю вне этого интервала:
b/2
0
-b/2
1/b

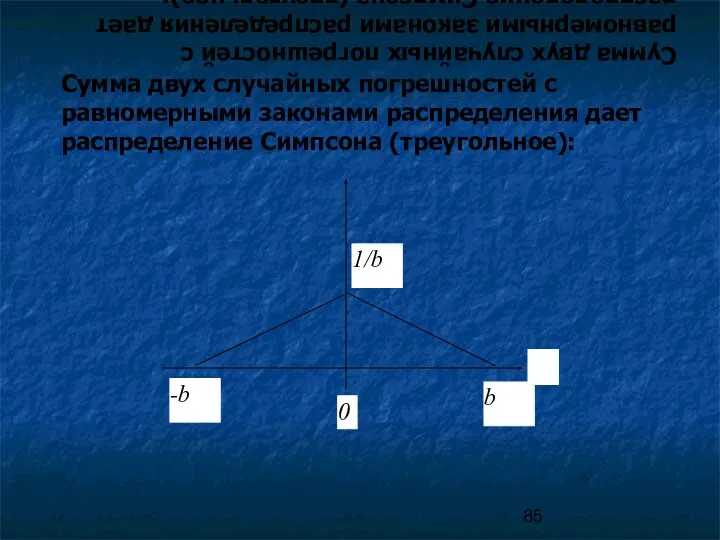
Сумма двух случайных погрешностей с равномерными законами распределения дает распределение Симпсона (треугольное):
Сумма двух случайных погрешностей с равномерными законами распределения дает распределение Симпсона (треугольное):

Обработка результатов измерений при наличии случайных погрешностей
Задача обработки заключается в том, чтобы по данным нескольких (n) таких измерений :
(А1 , А2 ,…Аn),
получить одно число Ах – результат измерения и оценить для него доверительный интервал случайной погрешности Δдов с указанием соответствующей доверительной вероятности Pдов .
Можно сформулировать три типичных ситуации такой обработки, различающиеся степенью наших априорных (до проведения опыта) знаний о законе распределения случайной погрешности.
Для упрощения будем предполагать, что мы имеем дело с нормальным законом распределения случайной погрешности.

1. Вид функции f (Δ) – известен ( нормальный закон),
параметр σ – известен, например, на основании предыдущих многократных наблюдений. Очевидно, что это достаточно определенная ситуация;
2. Вид функции f (Δ) – известен ( нормальный закон),
однако параметр σ – не известен - его надо будет найти по полученной выборке.
Естественно ожидать, что во второй ситуации доверительный интервал Δдов будет больше при той же доверительной вероятности Pдов
или
будет меньше вероятность Pдов при том же значении доверительного интервала Δдов.

Первая ситуация - самая простая – мы знаем о случайной величине все, что можно о ней знать. В этом ситуации можно сделать даже одно измерение (n=1), принять это значение А1 за результат,
выбрать значение доверительной вероятности Pдов ,
по таблице интеграла вероятностей определить соответствующе значение параметра KН,
,умножить его на известное значение σ и определить таким образом доверительный интервал:
Δдов = KH (Pдов) σ
и записать результат измерения:
При проведении простых технических измерений можно рекомендовать задавать значения Pдов порядка 0,8…0,9. Не следует использовать значения Pдов более 0,99!

Вполне возможно, что оцененная таким образом случайная погрешность результата измерений нас не устроит, - окажется слишком велика.
В этом случае надо провести n измерений:
A1, A2, A3…An
и найти среднее арифметическое этих значений. Доказано, что при нормальном распределении – это лучший способ распорядиться полученной выборкой.
С увеличением n среднее арифметическое значение стремится к математическому ожиданию, т.е. к истинному значению измеряемой величины:

Среднее арифметическое – это тоже нормально распределенная случайная величина. Поэтому решение задачи для первой типичной ситуации можно записать в виде:
Увеличение количества результатов измерений – это кардинальный путь уменьшения влияния случайных погрешностей. Разумеется, здесь есть ограничения, обусловленные требованием неизменности измеряемой величины в процессе получения выборки большого объема и независимости измерений в данной выборке.

Вторая типичная ситуация – имеем дело с нормальным законом распределения случайной погрешности, но параметр σ - неизвестен.
Делаем выборку объема n (A1, A2…An.),
рассчитываем среднее арифметическое значение,
рассчитываем так называемое выборочное среднеквадратическое отклонение однократного измерения:
которое представляет собой оценку неизвестного значения параметра σ.
Член ( n-1) в этом выражении математики называют числом степеней свободы.

Далее рассчитываем выборочное СКО среднего арифметического значения
и записываем результат:
где
- коэффициент, определяемый распределением Стьюдента.

1,96 ≈ 2 =KH(Pдов)
Таблицы коэффициентов
приводятся в справочниках. В частности, для Р=0,95 , коэффициенты Стьюдента определяются таблицей:
Поскольку при n →∞ t(n, Pдов) =KH (Pдов) ≈ 2
то для того, чтобы перейти от второй ситуации к первой, достаточно просто увеличить количество измерений! Но это не всегда возможно.

Третья типичная ситуация обработки характеризуется отсутствием информации о законе распределения погрешности, но есть основания считать, что такое распределение, в принципе, существует.
В этой ситуации необходимо выполнить достаточно много измерений заведомо неизменной величины и по этой большой выборке построить так называемую «гистограмму» опытного распределения случайной погрешности – экспериментальный аналог плотности вероятности этого распределения.

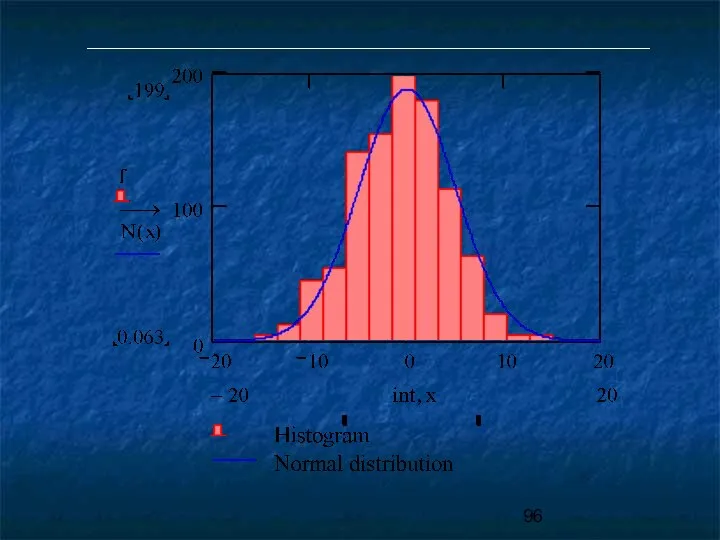
Для построения гистограммы всю область полученных значений погрешности
от Δmin до Δmax
разбивают на r одинаковых интервалов, количество которых выбирают по эмпирической формуле
r =(3…5)lg(n).
Далее подсчитывают количество значений погрешности, попавших в эти интервалы
n1, n2, …. nr.
По этим значениям строят ступенчатую зависимость – гистограмму

Визуально оценив гистограмму, можно предположить («выдвинуть статистическую гипотезу»), какому закону распределения случайной погрешности она может соответствовать. В математике разработаны процедуры проверки статистических гипотез, которые можно использовать для получения информации о законах распределения реальных случайных погрешностей.
Если принимается гипотеза нормального распределения, то можно перейти, как показано выше, от третьей ко второй и далее к первой ситуации обработки данных.

3.8. Систематические погрешности
Систематическую погрешность довольно трудно найти - для этого надо иметь оценку действительного значения измеряемой величины. Но если она найдена, ее можно исключить из результата измерения.
Общие способы обнаружения и исключения систематических погрешностей:
1. Проведение перед измерениями операции «установки 0» средства измерения - путем подачи на его вход сигнала с заведомо «нулевым» значением измеряемой величины - так можно обнаружить и исключить аддитивную составляющую систематической погрешности.

2.Проведение перед измерениями операции «калибровки» СИ – путем подачи на его вход сигнала с известными значениями измеряемой величины – так можно обнаружить и скомпенсировать мультипликативную составляющую систематической погрешности.

3. Использовать при измерениях два прибора одинаковой точности, но работающие на различных принципах. Существенное расхождение их показаний может говорить о наличии систематической погрешности неизвестного происхождения;
4. Применить способ компенсации систематической погрешности по знаку - так построить схему измерения, чтобы один раз систематическая погрешность входила в результат измерения с одним знаком, а второй раз - с противоположным.

5. Иногда хорошо работает способ «рандомизации» – превращения систематической погрешности в случайную, хотя практически реализовать это способ не так то просто. Случайная погрешность «лучше» систематической в том смысле, что ее можно уменьшить при увеличении количества измерений путем статистического усреднения.

3.9. Суммирование погрешностей
Систематические составляющие погрешности складывают алгебраически - с учетом знака:
Очевидно, что систематические погрешности могут друг друга частично или даже полностью компенсировать. Этим широко пользуются при конструировании СИ

Неисключенные систематические погрешности, задаваемые предельно допускаемыми интервалами, суммируют, как правило, по модулю, а знак “±” выносят за скобку:
Такой способ сложения используют, если число слагаемых не более трех.
При большем числе составляющих используют формулы, аналогичные формулам суммирования случайных погрешностей.

Результирующее СКО суммы случайных составляющих погрешностей определяют по формуле:
(т.е. складывают дисперсии – квадраты СКО).
Этой формулой можно пользоваться при произвольных законах распределения отдельных составляющих.
Однако доверительные интервалы суммировать по такой формуле в общем случае нельзя.

3.10. Погрешности косвенных измерений
Результат косвенных измерений может быть функцией как одной, так и нескольких переменных.
Простой пример - косвенные измерения периода сигнала T по результатам прямых измерений его частоты f (или наоборот).
Оценка погрешности частоты известна , период находим по формуле T=1/f .
Как определить погрешность оценки периода?

Чаще встречаются косвенные измерения, при которых искомая величина зависит от нескольких аргументов:
сопротивление R=U/I, мощность P=UI.
Погрешности прямых измерений напряжения и тока известны, надо оценить погрешности косвенных измерений R или P
Примером более сложной функциональной зависимости являются косвенные измерения индуктивности катушки:
Надо определить значение индуктивности L и погрешность измерения ΔL, если погрешности
Δf и ΔC0
известны - определены нормируемыми МХ прибора.

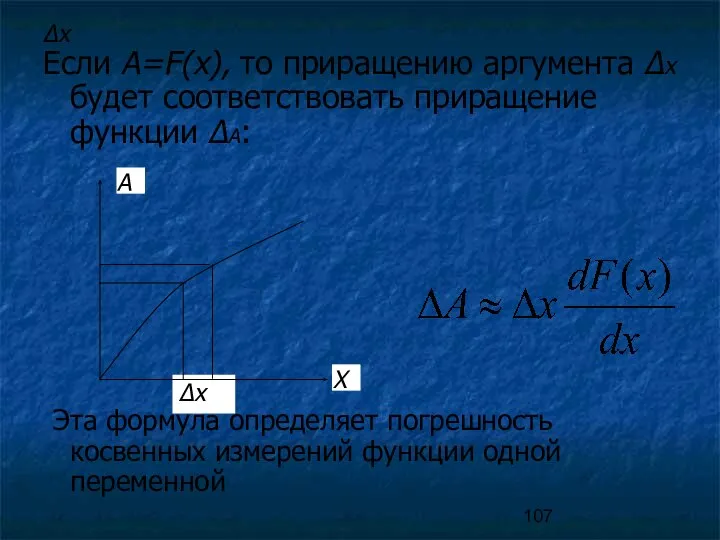
Δх
Если A=F(x), то приращению аргумента Δх будет соответствовать приращение функции ΔА:
Эта формула определяет погрешность косвенных измерений функции одной переменной

При выводе этой формулы не сделано никаких предположений о том, что за погрешность Δх - систематическая или случайная.
Очевидно, что если погрешность прямых измерений - систематическая, то надо учитывать ее знак и знак производной при определении погрешности .
Если погрешность аргумента случайная (или неисключенная систематическая) и задается симметричным интервалом ± Δх, то и погрешность косвенных измерений также будет определяться симметричным интервалом ±ΔА.

Если косвенно измеряемая величина является функцией нескольких переменных: A=F(x,y,t), то используя частные производные, следует получить формулы для частных погрешностей косвенных измерений, обусловленные наличием погрешностей прямых измерений значений аргументов функции:

Далее возникает задача суммирования этих частных погрешностей косвенных измерений.
При числе слагаемых не более трех результирующую погрешность косвенных измерений принято рассчитывать как сумму модулей частных погрешностей, а знак “±” выносить за скобку:
При числе слагаемых более трех обычно рекомендуют использовать квадратическое сложение - складывать квадраты частных погрешностей и из полученной суммы извлекать корень.

Рассмотрим практическую задачу косвенного определения периода по результатам прямых измерений частоты:
f=123456 Гц ±1Гц.
Это реальный результат, полученный с использованием электронно-счетного частотомера, а его погрешность ±1Гц – это погрешность квантования, которая принципиально имеет одну значащую цифру!
Период - величина, обратная частоте и значение
Т=1/f = 8,10005184033 мкс
нетрудно рассчитать на калькуляторе. Поскольку пока мы не знаем погрешности, то неизвестно, сколько значащих цифр оставить в расчетном значении Т.

Можно предложить три варианта расчета погрешности косвенных измерений периода:
1. Следует найти производную от функции 1/f и записать в общем виде выражение для абсолютной погрешности косвенных измерений периода:

Расчет дает значение 0,0000656 мкс, которое, в соответствии с правилами, следует округлить до одной значащей цифры: 0,00007 мкс.
Теперь можно записать результат косвенного измерения периода с указанием погрешности:
T= 8,10005 мкс ± 0,00007 мкс
- младший разряд значения погрешности определяет младший разряд результата косвенных измерений периода.

2. Второй вариант более наглядный - следует найти общее выражение для относительной погрешности косвенных измерений периода:
δТ = - δf .
В данном примере относительные погрешности частоты и периода равны по модулю и противоположны по знаку, что, вообще говоря, для данного примера достаточно очевидно и без всяких расчетов.
Однако при сложных формулах переход к относительным погрешностям позволяет, как правило, значительно упростить выражения для погрешности косвенных измерений, поскольку постоянные множители при этом сокращаются.

3. Наконец, наиболее прост третий способ - численной оценки погрешности косвенных измерений, который вообще не требует дифференцирования функции. Достаточно рассчитать два значения периода:
первое T1= 1/f и второе T2 =1/(f +Δf) т.е. с учетом положительного приращения частотыы, обусловленного погрешностью +1Гц. Разность T2 – T1 дает искомую погрешность косвенного измерения периода. Очевидно, что значение T3= 1/(f -Δf) можно не рассчитывать, поскольку в первом приближении, отклонения в обе стороны будут одинаковы по абсолютной величине.