- Главная
- Математика
- Свойство биссектрисы угла

Содержание
- 2. Свойство биссектрисы углы T Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Дано: ∠BAC; AM
- 3. Теорема о биссектрисах треугольника T Биссектрисы треугольника пересекаются в одной точке. Дано: ΔABC, AA1, BB1, CC1
- 4. Закрепление № 676 (а), 678 (а), 674
- 5. № 676 (а)
- 6. № 678 (а)
- 7. № 674
- 9. Скачать презентацию
Слайд 2Свойство биссектрисы углы
T Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Дано:
Свойство биссектрисы углы
T Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Дано:
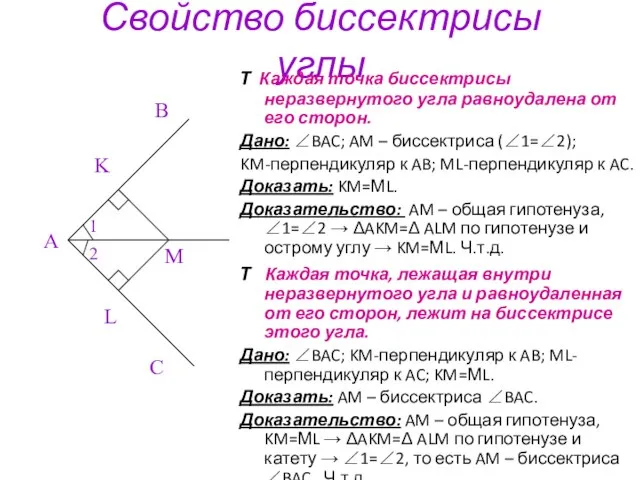
∠BAC; AM – биссектриса (∠1=∠2);
KM-перпендикуляр к AB; ML-перпендикуляр к AC.
Доказать: KM=МL.
Доказательство: AM – общая гипотенуза, ∠1=∠2 → ΔAKM=Δ ALM по гипотенузе и острому углу → KM=МL. Ч.т.д.
T Каждая точка, лежащая внутри неразвернутого угла и равноудаленная от его сторон, лежит на биссектрисе этого угла.
Дано: ∠BAC; KM-перпендикуляр к AB; ML-перпендикуляр к AC; KM=МL.
Доказать: AM – биссектриса ∠BAC.
Доказательство: AM – общая гипотенуза, KM=МL → ΔAKM=Δ ALM по гипотенузе и катету → ∠1=∠2, то есть AM – биссектриса ∠BAC . Ч.т.д.
KM-перпендикуляр к AB; ML-перпендикуляр к AC.
Доказать: KM=МL.
Доказательство: AM – общая гипотенуза, ∠1=∠2 → ΔAKM=Δ ALM по гипотенузе и острому углу → KM=МL. Ч.т.д.
T Каждая точка, лежащая внутри неразвернутого угла и равноудаленная от его сторон, лежит на биссектрисе этого угла.
Дано: ∠BAC; KM-перпендикуляр к AB; ML-перпендикуляр к AC; KM=МL.
Доказать: AM – биссектриса ∠BAC.
Доказательство: AM – общая гипотенуза, KM=МL → ΔAKM=Δ ALM по гипотенузе и катету → ∠1=∠2, то есть AM – биссектриса ∠BAC . Ч.т.д.
A
B
C
K
L
M
1
2
Слайд 3Теорема о биссектрисах треугольника
T Биссектрисы треугольника
пересекаются в одной точке.
Дано: ΔABC,
Теорема о биссектрисах треугольника
T Биссектрисы треугольника
пересекаются в одной точке.
Дано: ΔABC,
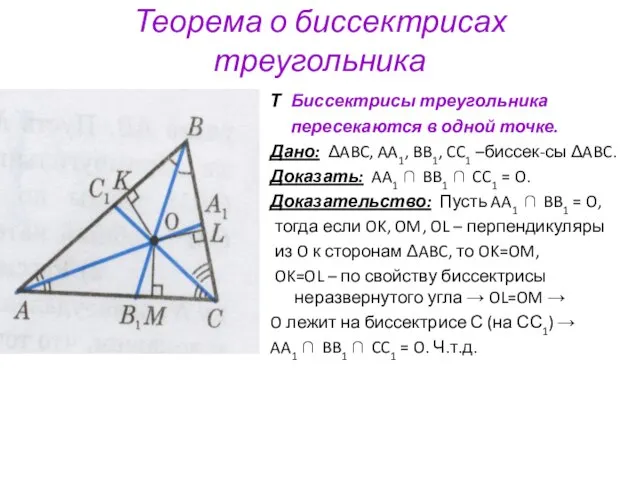
AA1, BB1, CC1 –биссек-сы ΔABC.
Доказать: AA1 ∩ BB1 ∩ CC1 = O.
Доказательство: Пусть AA1 ∩ BB1 = O,
тогда если OK, OM, OL – перпендикуляры
из O к сторонам ΔABC, то OK=OM,
OK=OL – по свойству биссектрисы неразвернутого угла → OL=OM →
O лежит на биссектрисе С (на СС1) →
AA1 ∩ BB1 ∩ CC1 = O. Ч.т.д.
Доказать: AA1 ∩ BB1 ∩ CC1 = O.
Доказательство: Пусть AA1 ∩ BB1 = O,
тогда если OK, OM, OL – перпендикуляры
из O к сторонам ΔABC, то OK=OM,
OK=OL – по свойству биссектрисы неразвернутого угла → OL=OM →
O лежит на биссектрисе С (на СС1) →
AA1 ∩ BB1 ∩ CC1 = O. Ч.т.д.
Слайд 4Закрепление
№ 676 (а), 678 (а), 674
Закрепление
№ 676 (а), 678 (а), 674

Слайд 5№ 676 (а)
№ 676 (а)
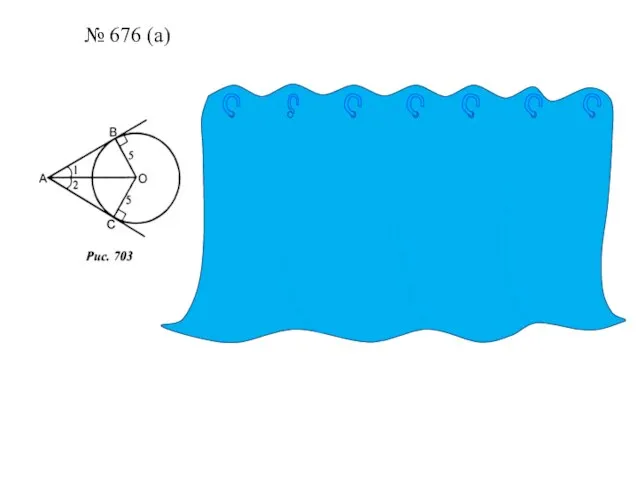
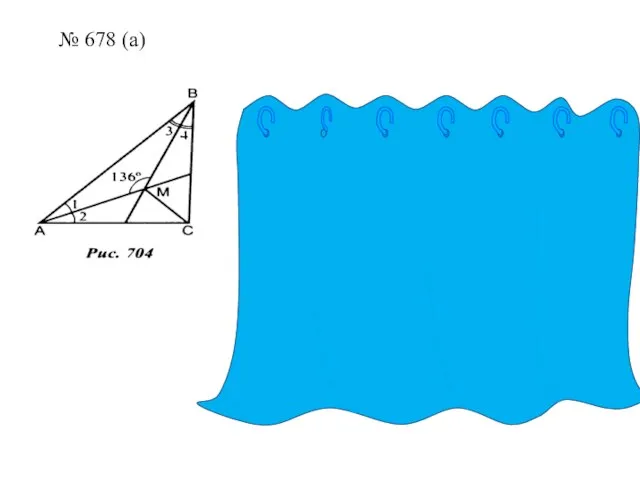
Слайд 6№ 678 (а)
№ 678 (а)
Слайд 7№ 674
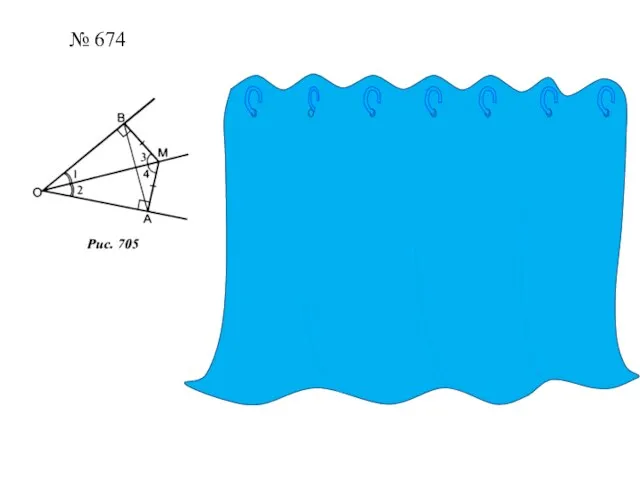
№ 674
- Предыдущая
Trzej synowie Построение графиков в MathCAD
Построение графиков в MathCAD Квадратичная функция. Решение текстовых задач
Квадратичная функция. Решение текстовых задач Многогранники: выпуклые призмы и антипризмы
Многогранники: выпуклые призмы и антипризмы Презентация по математике "Логарифмическая функция. Преобразования графиков." -
Презентация по математике "Логарифмическая функция. Преобразования графиков." -  Вычисление определенных интегралов
Вычисление определенных интегралов Это полезно знать. Интересные факты из жизни самых больших чисел
Это полезно знать. Интересные факты из жизни самых больших чисел Множество и его элементы
Множество и его элементы Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Площадь фигур. Свойства площадей
Площадь фигур. Свойства площадей Математический турнир Умники и умницы
Математический турнир Умники и умницы Презентация на тему Рещение линейных уравнений
Презентация на тему Рещение линейных уравнений  Игра - путешествие В стране занимательной математики
Игра - путешествие В стране занимательной математики Математическая грамотность. Урок 1
Математическая грамотность. Урок 1 Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Параллелограмм и трапеция. Урок 4
Параллелограмм и трапеция. Урок 4 Теорема Пифагора
Теорема Пифагора Презентация по математике "Правило умножения для комбинаторных задач" -
Презентация по математике "Правило умножения для комбинаторных задач" -  Вычисление производных. Формулы дифференцирования
Вычисление производных. Формулы дифференцирования Упрощение логических выражений
Упрощение логических выражений Системы неравенств с двумя переменными
Системы неравенств с двумя переменными Поиск сокровищ. Изучений геометрических фигур
Поиск сокровищ. Изучений геометрических фигур Деление суммы на число
Деление суммы на число Презентация на тему Умножение двузначного числа на однозначное (3 класс)
Презентация на тему Умножение двузначного числа на однозначное (3 класс)  Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Презентация на тему Перебор возможных вариантов
Презентация на тему Перебор возможных вариантов  Степень с отрицательным показателем
Степень с отрицательным показателем