Содержание
- 2. Комбинаторика и вероятность. В теории вероятности ключевым понятием является случайность, понятие довольно таки абстрактное. Казалось бы,
- 3. Комбинаторика и вероятность. Давайте разберем, как формулы комбинаторики помогают при вычислении вероятности событий. Чтобы глубоко не
- 4. Комбинаторика и вероятность. Пример. Из колоды карт (36 карт) случайным образов вытаскивают 4 карты. Найти вероятность
- 5. Комбинаторика и вероятность. б) В этом пункте нас просят найти вероятность события, обратного событию предыдущей задачи.
- 6. Комбинаторика и вероятность. Пример. В урне лежат красные и синие шары. Известно, что красных шаров 8
- 7. Комбинаторика и вероятность. а) Мы вытаскиваем 3 шара, причем из них должно оказаться ровно 2 синих,
- 8. Комбинаторика и вероятность. б) Посмотрим внимательно на условие: Среди вытащенных шаров не меньше одного красного. Это
- 9. Комбинаторика и вероятность. в) Вероятность того, что синих шаров вытащили больше чем красных означает, что было
- 10. Комбинаторика и вероятность. В конце урока отметим, что вероятностные задачи решать тяжелее, чем просто комбинаторные. В
- 12. Скачать презентацию









 Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2 Математика вокруг нас
Математика вокруг нас Комбинаторика
Комбинаторика Старинные задачи на дроби
Старинные задачи на дроби Умножение нуля и единицы
Умножение нуля и единицы Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Правильные многогранники вокруг нас
Правильные многогранники вокруг нас Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Решение примеров и простых задач в пределах 10
Решение примеров и простых задач в пределах 10 Сечения куба плоскостью
Сечения куба плоскостью координаты вектора
координаты вектора Системы линейных уравнений СЛУ
Системы линейных уравнений СЛУ Геометрическая прогрессия
Геометрическая прогрессия Луч и отрезок
Луч и отрезок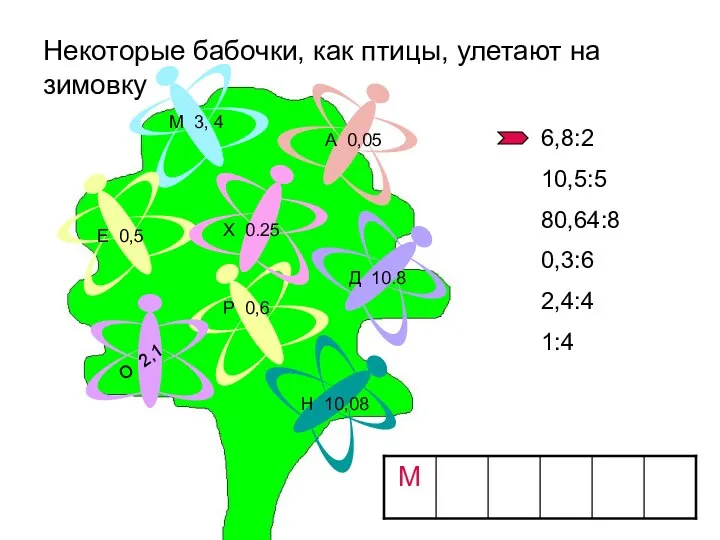 Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку
Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку Многочлен. Решить задачу
Многочлен. Решить задачу Презентация на тему Решение текстовых задач различными способами
Презентация на тему Решение текстовых задач различными способами  Многогранники. Задания
Многогранники. Задания Координаты вектора
Координаты вектора Координатная плоскость
Координатная плоскость Решение логарифмических неравенств
Решение логарифмических неравенств Среднее арифметическое
Среднее арифметическое Презентация на тему Решение задач по теме "Пирамида" 10 класс
Презентация на тему Решение задач по теме "Пирамида" 10 класс  Прямой угол
Прямой угол Вектор. Равенство векторов
Вектор. Равенство векторов Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации