Првильные многоугольники

Работаем по учебнику
С 275
1. Найдите определение правильного многоугольника.

Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны

2. Выпишите формулу суммы внутренних углов выпуклого многоугольника.

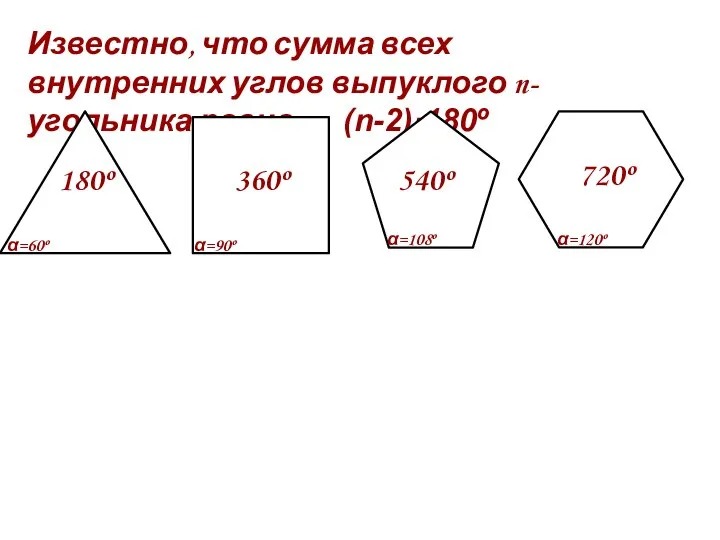
Известно, что сумма всех внутренних углов выпуклого n-угольника равна (n-2)·180º
α=60º
α=90º
α=108º
α=120º
180º
360º
540º
720º

3. Как вычислить градусную меру угла правильного многоугольника?

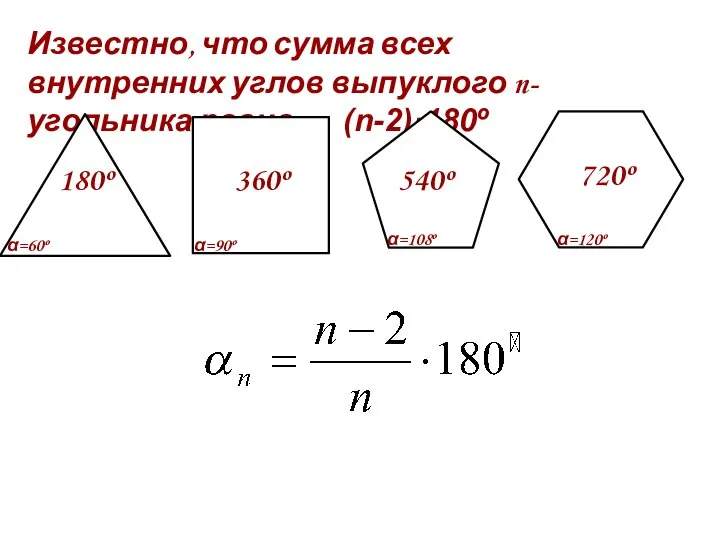
Известно, что сумма всех внутренних углов выпуклого n-угольника равна (n-2)·180º
α=60º
α=90º
α=108º
α=120º
180º
360º
540º
720º

4. Что такое описанная окружность?
5. Как построить центр описанной около правильного многоугольника окружности?

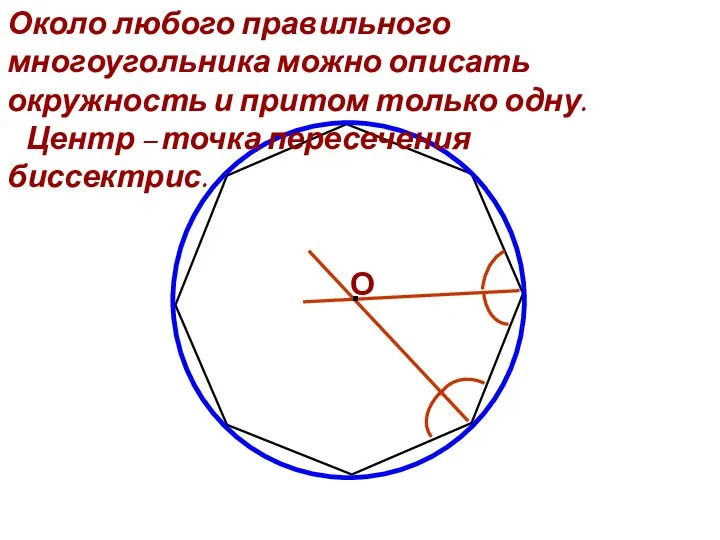
Около любого правильного многоугольника можно описать окружность и притом только одну.
Центр – точка пересечения биссектрис.
·
О

6. Что такое вписанная окружность?
7. Как построить центр вписанной в правильный многоугольник окружности?

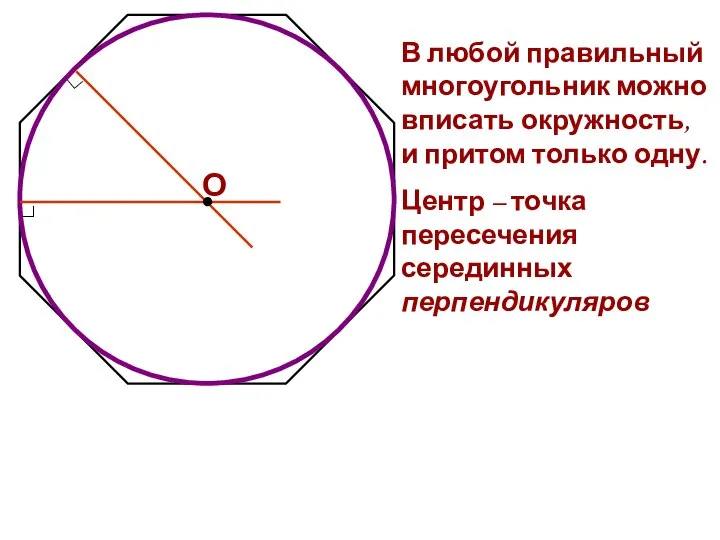
В любой правильный многоугольник можно вписать окружность, и притом только одну.
Центр – точка пересечения серединных перпендикуляров
•
О
∟
∟

8. Верно-ли утверждение?
1. Окружность вписанная в многоугольник, касается его сторон в их серединах.
2.Центр описанной и вписанной окружностей для многоугольника совпадают.

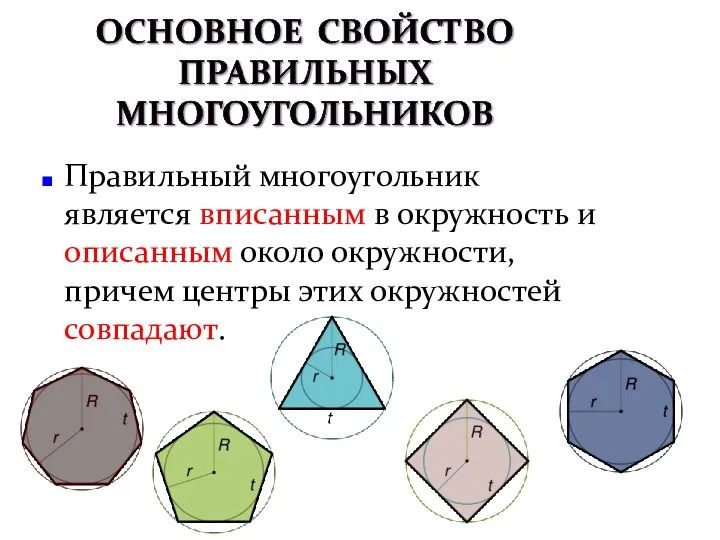
Правильный многоугольник является вписанным в окружность и описанным около окружности, причем центры этих окружностей совпадают.

9. Что такое центр правильного многоугольника?
10. Существует ли центр произвольного многоугольника

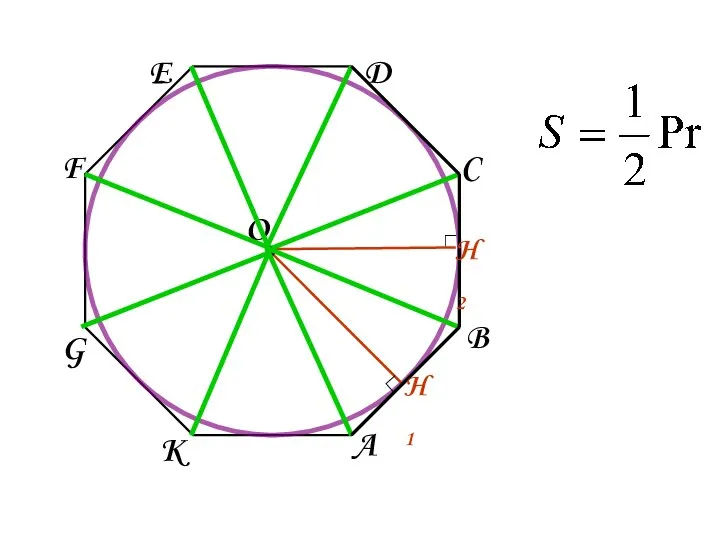
11. Как найти площадь правильного многоугольника?

•
∟
∟
A
B
C
D
E
F
G
K
H1
H2
O

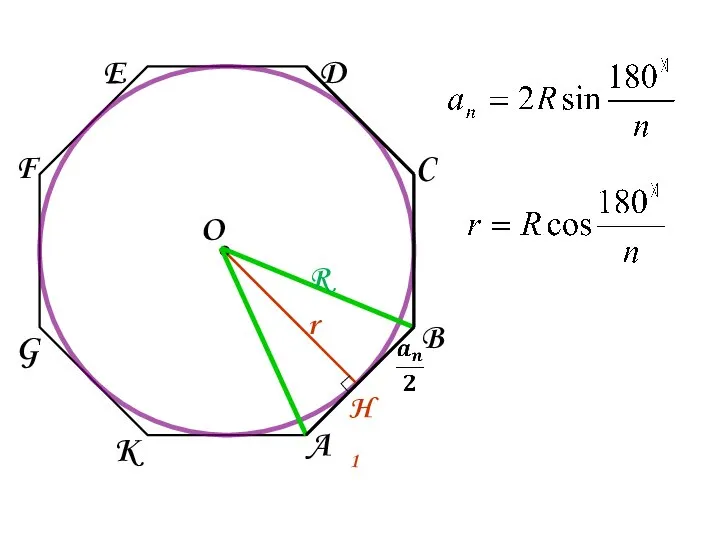
12. Выразите сторону правильного многоугольника через радиус описанной окружности.
13. Выразите радиус вписанной в правильный многоугольник окружности через радиус описанной окружности.

•
∟
A
B
C
D
E
F
G
K
H1
O
R
r