Слайд 2Некоторые понятия и определения
1. Ненулевой вектор n, перпендикулярный заданной прямой, называется нормальным

вектором для этой прямой.
Слайд 3Некоторые понятия и определения

Слайд 4Некоторые понятия и определения

Слайд 5Способы задания прямой на плоскости
1. По точке и нормальному вектору
2. По точке

и направляющему вектору
3. По двум точкам
Слайд 7Метрические приложения уравнений прямых на плоскости

Слайд 8Метрические приложения уравнений прямых на плоскости

Слайд 9Метрические приложения уравнений прямых на плоскости

Слайд 11Составить каноническое, параметрическое, общее, нормированное и уравнение прямой в отрезках
Дано; A(1,2)

B(4,6)
Слайд 12Составить уравнение с угловым коэффициентом

Слайд 13Вычислить:
ж) расстояние от прямой до начала координат ;
з) площадь треугольника, образованного

этой прямой с координатными осями;
и) величину угла между этой прямой и положительным направлением оси абсцисс
Слайд 15Алгоритм нахождения общего уравнение серединного перпендикуляра к стороне треугольника
1. Находим координаты точки

М- середины стороны
2. Искомый серединный перпендикуляр MN проходит через точку M перпендикулярно вектору (стороне треугольника). Находим координаты стороны. BC – нормаль для серединного перпендикуляра.
3. Запишем общее уравнение нормали с неизвестным свободным членом:
Ax+By+C=0
4. Свободный член С выбираем так, чтобы серединный перпендикуляр проходил через точку М. Подставляем вместо x и y координаты точки М. Находим значение С.
5. Записываем общее уравнение серединного перпендикуляра.
Слайд 16Нахождение общего уравнения серединного перпендикуляра к стороне
Дано; A(1,5) B(13,0), C( 5,8)

Слайд 17 Составить каноническое уравнение прямой, содержащей медиану AM. Составить общее уравнение прямой,

содержащей высоту AH.
Дано; A(1,5) B(13,0), C( 5,8) BC(-8,8)
Слайд 18Составить параметрическое уравнение прямой, содержащей биссектрису AL

Слайд 19Найти расстояние от вершины до прямой (т.е. высоту треугольника)

Слайд 20Найти величину угла между прямыми

Слайд 21Алгоритм нахождения координат точки ,
симметричной точке относительно прямой
1. Составляем уравнение

общее уравнение прямой.
Если известен направляющий вектор, то сначала записываем каноническое уравнение прямой, а затем общее уравнение прямой. Коэффициенты перед x и y - это координаты нормального вектора прямой.
2. Составляем параметрическое уравнение прямой ОО”, проходящей через начало координат, перпендикулярно АВ. Направляющий вектор этой прямой перпендикулярен вектору AB. Этот вектор находится из условия (p,AB)=0.
3.Записываем параметрическое уравнение прямой (выражение x и y через параметр t).
4. Подставляем выражения x и y в общее уравнения прямой.
5.Находим параметр t.
6.Подставляем его в параметрическое уравнение. Это есть координаты точки, симметричной относительно заданной прямой




















 Деление натуральных чисел
Деление натуральных чисел Следствия из аксиом I - III
Следствия из аксиом I - III Квадратичная функция проверочная работа
Квадратичная функция проверочная работа Презентация по математике "Город арифметика" -
Презентация по математике "Город арифметика" -  Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Парная регрессия и корреляция. Тема 2
Парная регрессия и корреляция. Тема 2 Предел функции в точке и на бесконечности
Предел функции в точке и на бесконечности Свойства сложения и умножения - Презентация_
Свойства сложения и умножения - Презентация_ Презентация на тему Дробные числа
Презентация на тему Дробные числа  Окружность и круг
Окружность и круг Классификация понятий. Правила классификации. Задания на сообразительность
Классификация понятий. Правила классификации. Задания на сообразительность Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Многогранники. Стереометрия
Многогранники. Стереометрия Вычисление пределов функций
Вычисление пределов функций Что такое проекция вектора
Что такое проекция вектора Что? Где? Когда?
Что? Где? Когда? ЕГЭ по математике. Экономические задачи VII
ЕГЭ по математике. Экономические задачи VII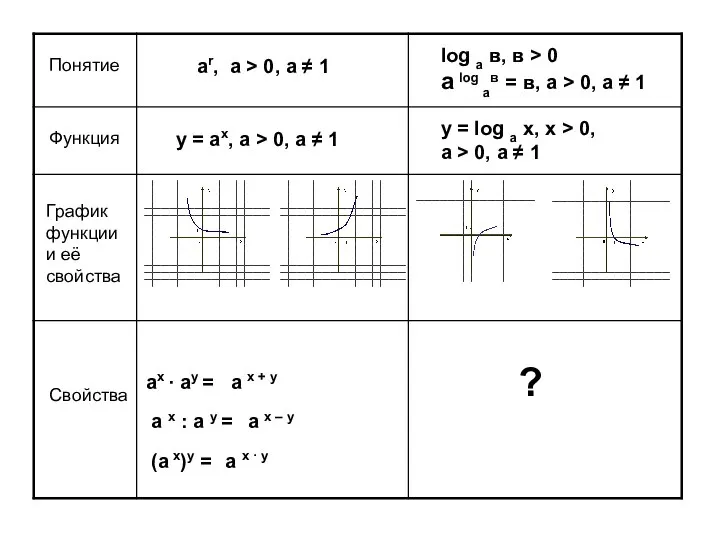 Свойства логарифмов
Свойства логарифмов Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком  Треугольники
Треугольники Рівняння руху гіроскопу в кардановому підвісі
Рівняння руху гіроскопу в кардановому підвісі Квадрат суммы и квадрат разности
Квадрат суммы и квадрат разности Урок математики 13.09
Урок математики 13.09 Математическая викторина
Математическая викторина Симметрическая и знакопеременная группы. Алгебраические операции
Симметрическая и знакопеременная группы. Алгебраические операции Задания со спичками
Задания со спичками Математический диктант по теме Простейшие задачи в координатах
Математический диктант по теме Простейшие задачи в координатах Интеграл. Определенный интеграл. Свойства
Интеграл. Определенный интеграл. Свойства