Содержание
- 2. План лекции
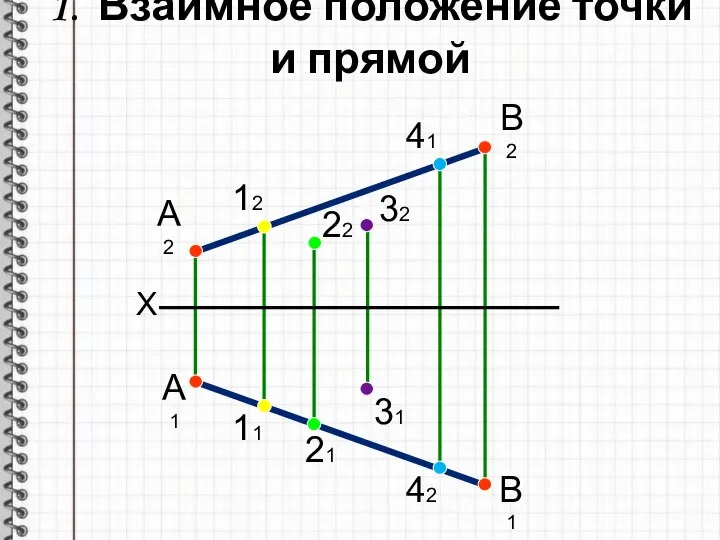
- 3. 1. Взаимное положение точки и прямой X А2 В2 А1 В1 12 11 22 21 32
- 4. Если точка принадлежит прямой, то проекции точки принадлежат одноименным проекциям прямой 1. Взаимное положение точки и
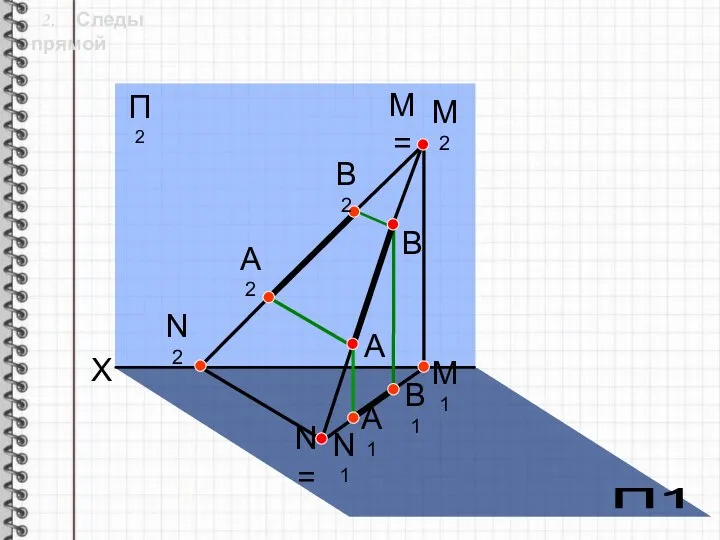
- 5. 2. Следы прямой Определение: След прямой - точка пересечения прямой с плоскостью проекций.
- 6. 2. Следы прямой X А1 В А В1 А2 В2 N= N1 N2 M2 M= M1
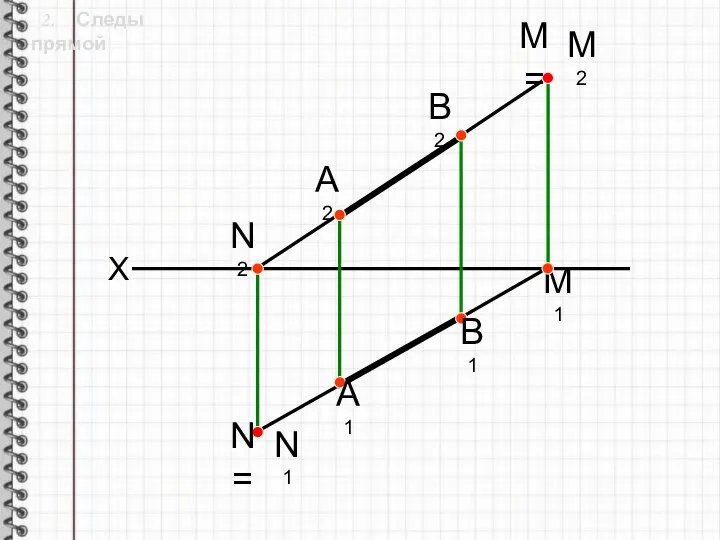
- 7. 2. Следы прямой А1 В1 А2 N= N1 N2 M2 M1 B2 X M=
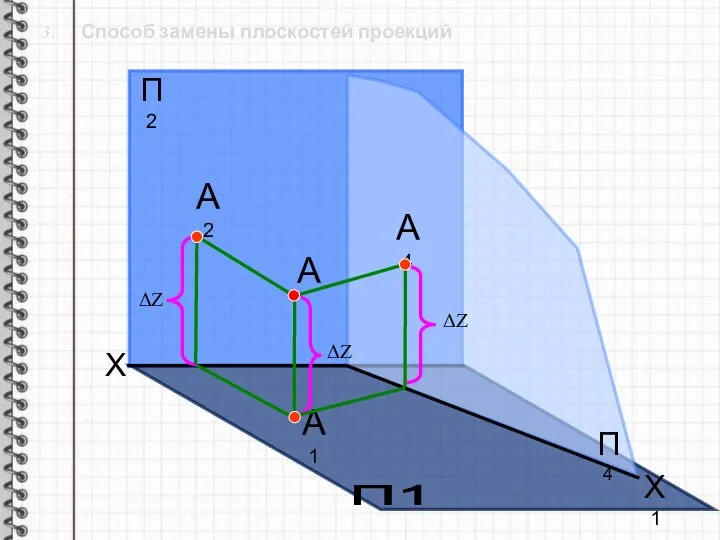
- 8. 3. Способ замены плоскостей проекций Способ замены плоскостей проекций заключается в последовательной замене одной из плоскостей
- 9. 3. Способ замены плоскостей проекций При этом должны быть выдержаны следующие условия: 1. Новая плоскость должна
- 10. 3. Способ замены плоскостей проекций X П2 П1 А1 А А2 П4 Х1 А4 ΔΖ ΔΖ
- 11. 3. Способ замены плоскостей проекций X П2 П1 П4 Х1
- 12. 3. Способ замены плоскостей проекций X П2 П1 Х1 П4
- 13. 3. Способ замены плоскостей проекций X П2 П1 Х1 П4
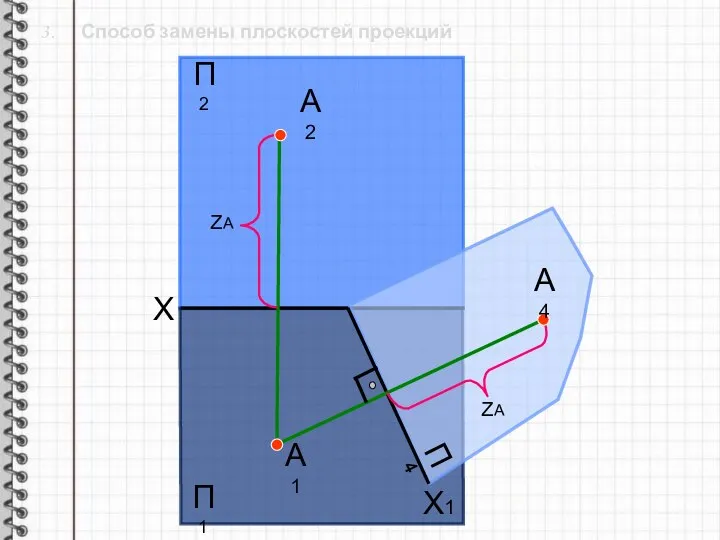
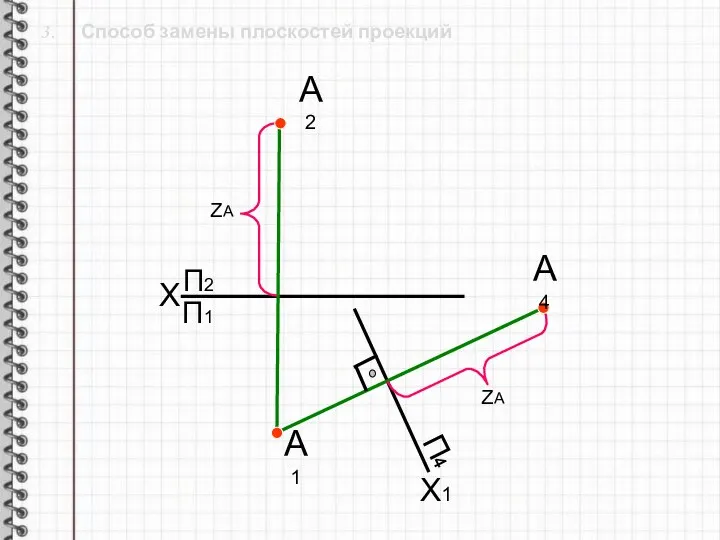
- 14. 3. Способ замены плоскостей проекций X П2 Х1 П1 П4 А1 А2 ZА ZА А4
- 15. 3. Способ замены плоскостей проекций X П2 Х1 П1 П4 А1 А2 ZА ZА А4
- 16. 4. Преобразование чертежа прямой Прямая общего положения может быть преобразована в: 1. прямую уровня; 2. проецирующую
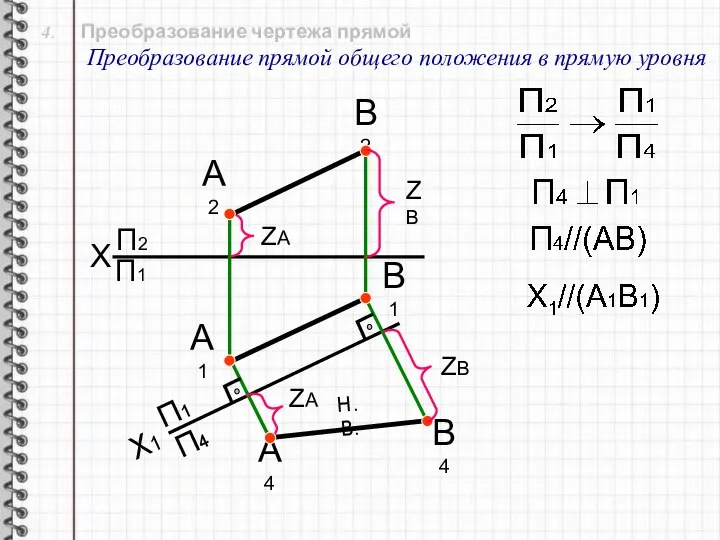
- 17. 4. Преобразование чертежа прямой Преобразование прямой общего положения в прямую уровня X П2 Х1 П1 П4
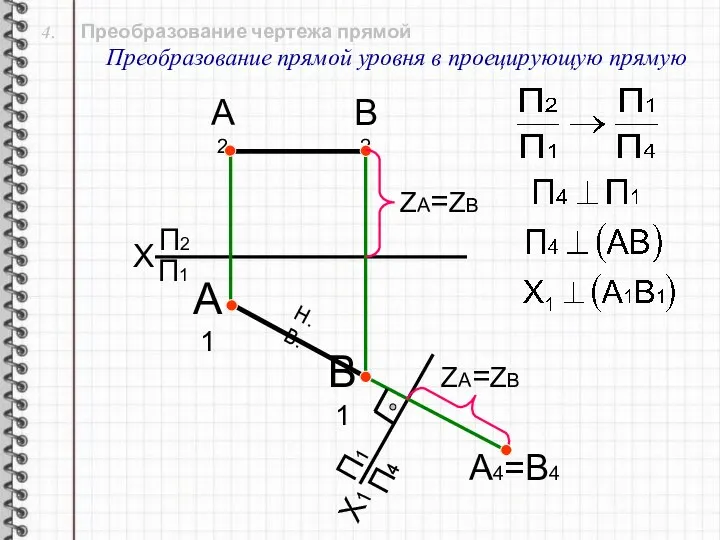
- 18. 4. Преобразование чертежа прямой Преобразование прямой уровня в проецирующую прямую X П2 Х1 П1 П4 А1
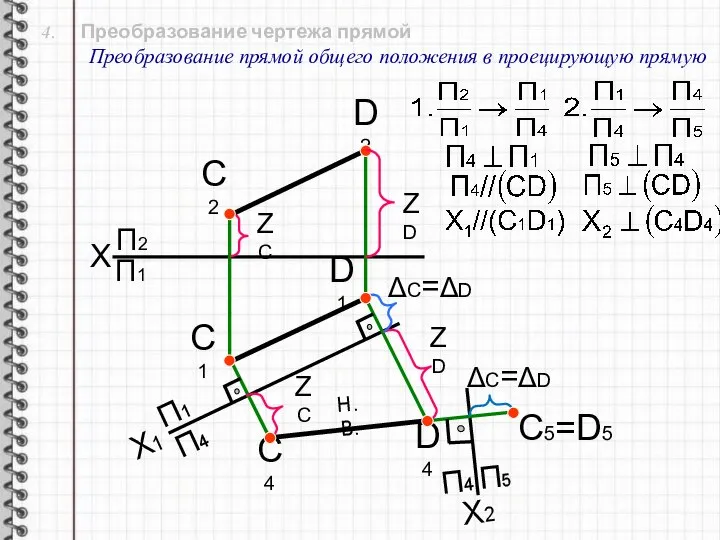
- 19. 4. Преобразование чертежа прямой Преобразование прямой общего положения в проецирующую прямую X П2 Х1 П1 П4
- 20. 5. Взаимное положение двух прямых Прямые в пространстве могут быть: пересекающимися; скрещивающимися; параллельными (в частности совпадать).
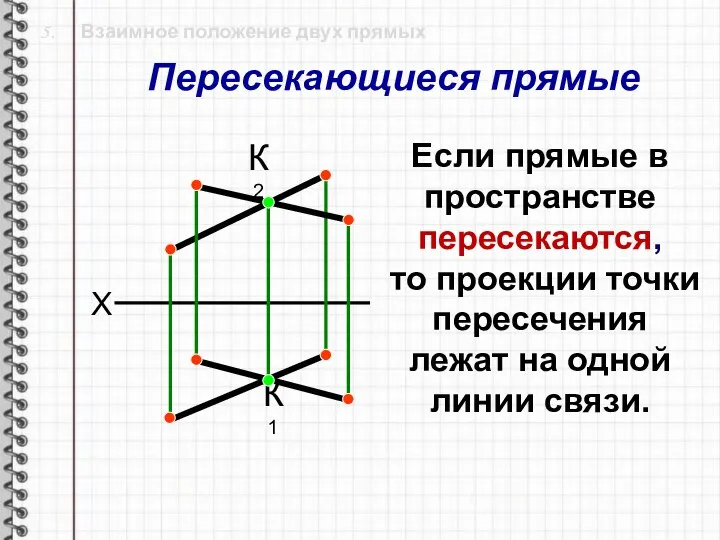
- 21. 5. Взаимное положение двух прямых К1 К2 X Если прямые в пространстве пересекаются, то проекции точки
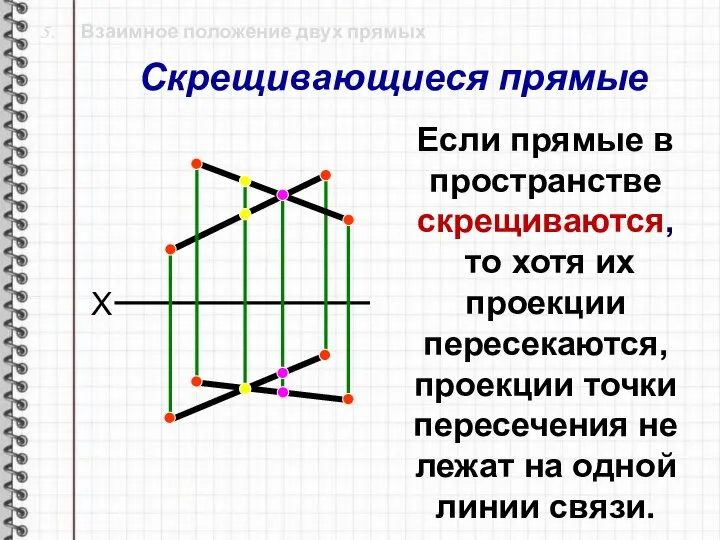
- 22. 5. Взаимное положение двух прямых X Если прямые в пространстве скрещиваются, то хотя их проекции пересекаются,
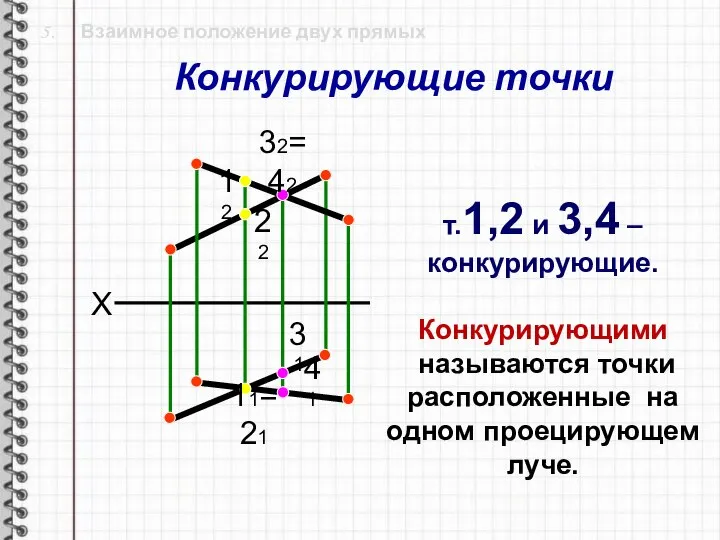
- 23. 5. Взаимное положение двух прямых X т.1,2 и 3,4 – конкурирующие. Конкурирующими называются точки расположенные на
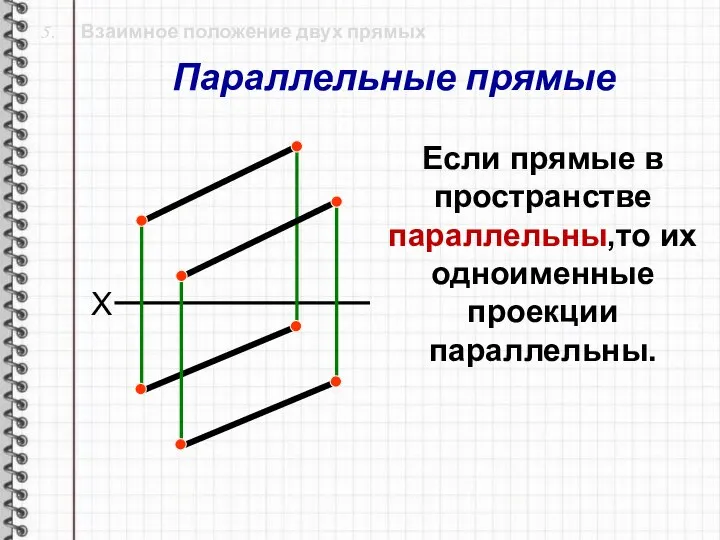
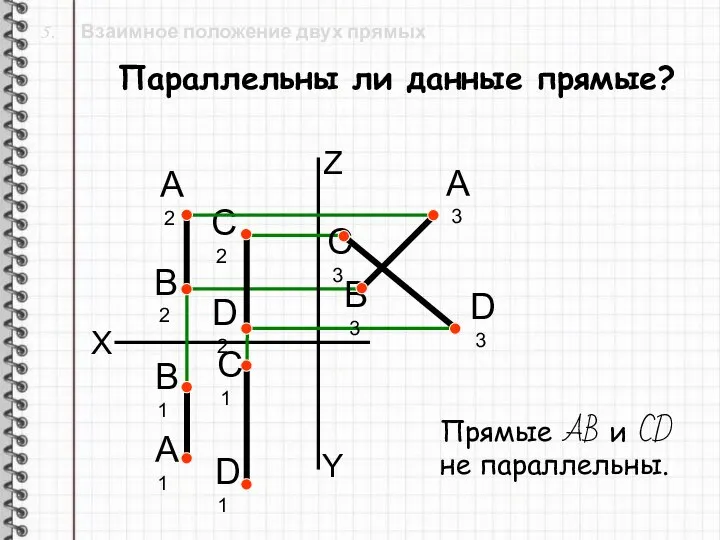
- 24. 5. Взаимное положение двух прямых X Если прямые в пространстве параллельны,то их одноименные проекции параллельны. Параллельные
- 25. 5. Взаимное положение двух прямых X Параллельны ли данные прямые? Z Y B1 B2 A1 D1
- 26. 6. Проекции плоских углов В зависимости от положения сторон плоского угла по отношению к плоскости проекций
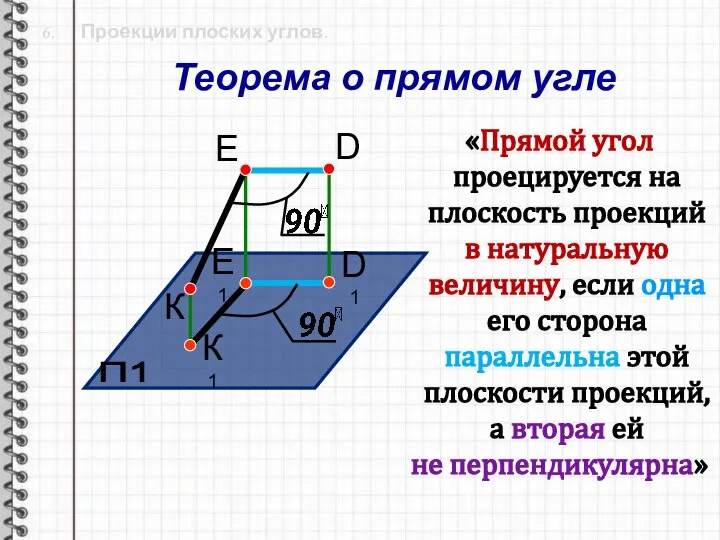
- 27. 6. Проекции плоских углов. «Прямой угол проецируется на плоскость проекций в натуральную величину, если одна его
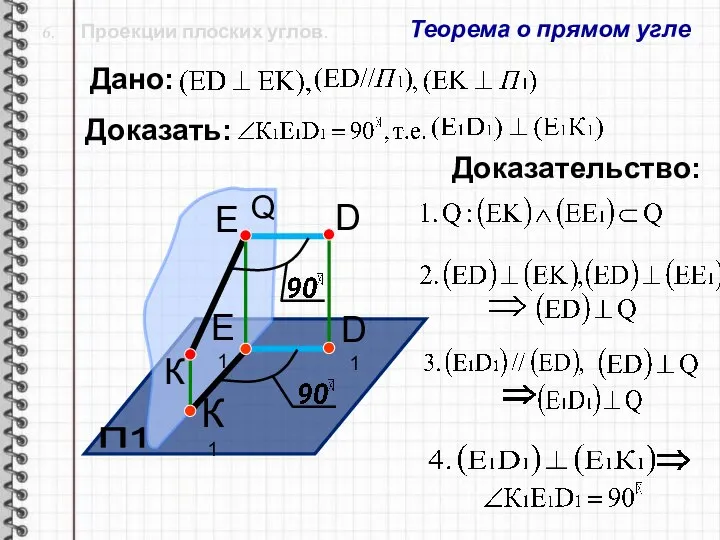
- 28. 6. Проекции плоских углов. Теорема о прямом угле П1 D1 D К1 Дано: Доказать: Доказательство: Q
- 30. Скачать презентацию








 Углы. Виды углов
Углы. Виды углов Ключевые задачи по теме пирамида
Ключевые задачи по теме пирамида Как можно сравнивать размеры больших и малых тел
Как можно сравнивать размеры больших и малых тел Свойства степени
Свойства степени Презентация на тему УСТНЫЙ СЧЕТ
Презентация на тему УСТНЫЙ СЧЕТ  Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Подготовка к диагностической работе. 5 класс
Подготовка к диагностической работе. 5 класс Геометрическая прогрессия. Задачи в формате экзамена
Геометрическая прогрессия. Задачи в формате экзамена Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса)
Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса) Логарифмические функции
Логарифмические функции Основные принципы комбинаторики
Основные принципы комбинаторики Построение и анализ графиков в среде Живая геометрия. 9 класс
Построение и анализ графиков в среде Живая геометрия. 9 класс Определение медианы
Определение медианы Презентация на тему Параллельность прямых
Презентация на тему Параллельность прямых  Презентация на тему Вводный урок математики в 5 классе
Презентация на тему Вводный урок математики в 5 классе  Решение тригонометрических неравенств
Решение тригонометрических неравенств Логарифмы вокруг нас
Логарифмы вокруг нас Построение графиков функций. Алгебра и начала анализа 11 класс
Построение графиков функций. Алгебра и начала анализа 11 класс Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Устный счет
Устный счет Пушкин и математика Выполнила ученица 10 «а» класса МОУ «Гимназия №58» г. Саратов Гаврилюк Виктория Владимировна, Регион – Сарато
Пушкин и математика Выполнила ученица 10 «а» класса МОУ «Гимназия №58» г. Саратов Гаврилюк Виктория Владимировна, Регион – Сарато Пирамида. Основание пирамиды
Пирамида. Основание пирамиды Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве Таблица сложения в пределах 20
Таблица сложения в пределах 20 Квадратичная функция
Квадратичная функция Презентация на тему Дециметр (1 класс)
Презентация на тему Дециметр (1 класс)  Показательное неравенство af(x) > a8(x)
Показательное неравенство af(x) > a8(x) Интеграл. Что называют криволинейной
Интеграл. Что называют криволинейной