Слайд 2КОНУС
Ко́нус (от др.-греч, κώνος «шишка») — тело, полученное объединением всех лучей, исходящих

из одной точки (вершины конуса) и проходящих через плоскую поверхность. Также можно сказать, что это тело, полученное при вращении прямоугольного треугольника вокруг одного из его катетов.
Слайд 3КОНУС
S пол=S бок +S осн
S бок= πrl
S осн= πr2
V=1/3S осн
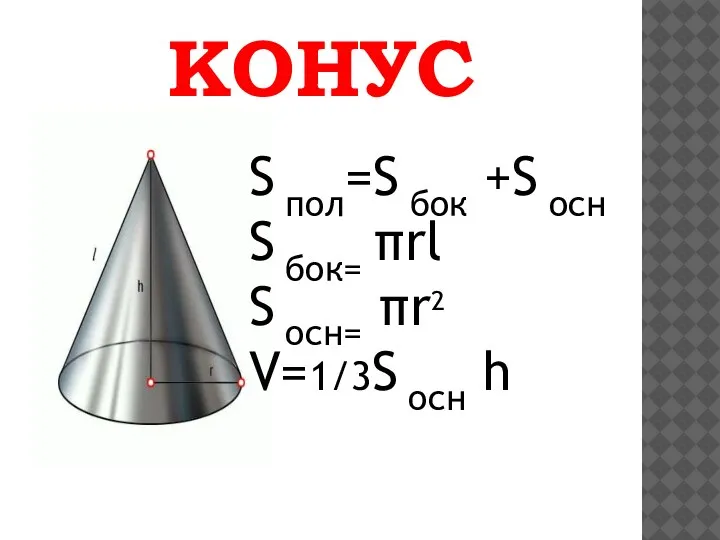
h
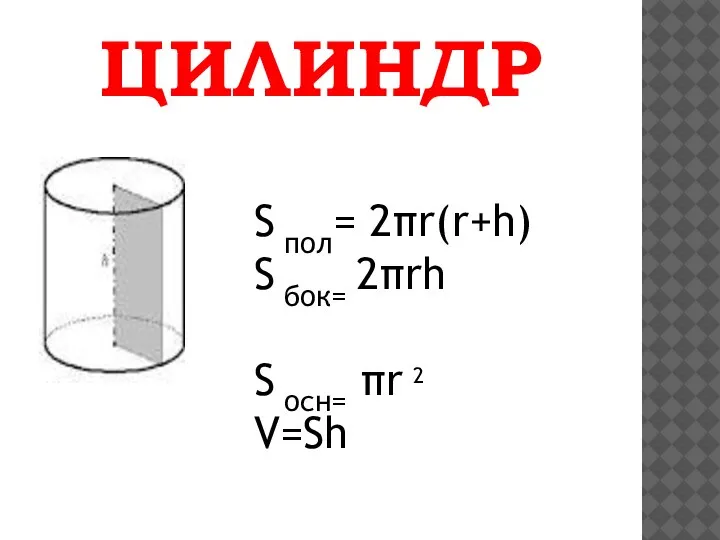
Слайд 5ЦИЛИНДР
Цили́ндр (др.-греч, κύλινδρος — валик, каток) —геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными

плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра.
У цилиндра имеется ось симметрии
Слайд 6ЦИЛИНДР
S пол= 2πr(r+h)
S бок= 2πrh
S осн= πr 2
V=Sh
Слайд 8ШАР
Шар - это пространственная фигура. Отрезок, соединяющий две точки сферы и проходящий

через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.
Любое сечение шара имеет вид круга. Если рассекать шар ближе к центру, то круги будут больше, если дальше от центра, то радиусы кругов будут меньше.
Арбуз, апельсин, Солнце, Луна, Земля и остальные планеты имеют форму немного сплющенного шара.
V=2/3πr2h
Слайд 9CФЕРА
Поверхность шара называют сферой.
Слово "сфера" произошло от греческого слова "сфайра", которое

переводится на русский язык как "мяч".
Сфера - это, можно сказать, оболочка или граница шара.
Мяч, глобус - это сферы.
Сфера обладает очень интересным свойством - все её точки одинаково удалены от центра шара.
Отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара. На рисунке отрезки ОА, ОВ, ОD и ОС являются радиусами .









 Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов
Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов 11 клас призма
11 клас призма Четные и нечетные числа
Четные и нечетные числа Решение уравнений и задач
Решение уравнений и задач Функциональная грамотность: формирование, диагностика
Функциональная грамотность: формирование, диагностика Презентация на тему Площади многоугольников
Презентация на тему Площади многоугольников  Понятие предиката и кванторы. Логические операции над предикатами
Понятие предиката и кванторы. Логические операции над предикатами Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Конспект урока по математике во 2 классе.
Конспект урока по математике во 2 классе. Параллельные прямые
Параллельные прямые Решение систем уравнений и неравенств графическим способом
Решение систем уравнений и неравенств графическим способом Что умеет линейка?
Что умеет линейка? Элементы теории вероятности в практических задачах
Элементы теории вероятности в практических задачах Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5?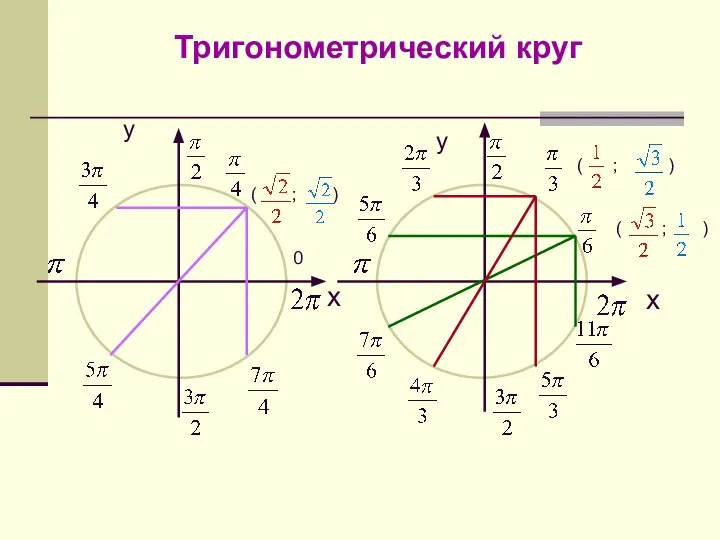 Тригонометрический круг
Тригонометрический круг Правильные многоугольники
Правильные многоугольники Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок)
Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок) Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах Квадратный трёхчлен и его корни
Квадратный трёхчлен и его корни predmet_stereometrii._aksiomy_stereometrii
predmet_stereometrii._aksiomy_stereometrii Число семь. Цифра 7
Число семь. Цифра 7 Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Координаты вектора
Координаты вектора Обозначение и сравнение углов
Обозначение и сравнение углов Таблица умножения с 7 до 9
Таблица умножения с 7 до 9 Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Статистическое наблюдение
Статистическое наблюдение