Слайд 2Определение
Неравенства вида
ax² + bx + c > 0 ; ax²

+ bx + c < 0,
(ax² + bx + c ≥ 0; ax² + bx + c ≤ 0)
неравенства второй степени с одной переменной или
квадратные неравенства
Слайд 3Метод ИНТЕРВАЛОВ
1) Найти корни соответствующего
квадратного уравнения
ах²+вх+с = 0

Слайд 4Метод ИНТЕРВАЛОВ
2) Корни уравнения нанести на числовую ось;
3) Разделить числовую ось на

интервалы;
4) Определить знаки функции в каждом из интервалов (…);
5) Выбрать подходящие интервалы и записать ответ.
Слайд 5х² + х – 6 ≥ 0
Решение:
1) решим соответствующее квадратное

уравнение
х² + 5х – 6 = 0
Т.к. а+в+с=0, то х₁ =1, а х₂ = - 6
Слайд 6
2) -6 1 х
3) Запишем ответ:
(-∞; -6]U[1;
![2) -6 1 х 3) Запишем ответ: (-∞; -6]U[1; +∞) 0 +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1142901/slide-5.jpg)
Слайд 7Решаем
1) х(х+7)≥0;
2) (х-1)(х+2)≤0;
3) х- х²+2<0;
4) -х²- 5х+6>0;
5) х(х+2)<15

Слайд 8Графический способ
1).Определить направление ветвей параболы, по знаку первого коэффициента квадратичной функции.
2).Найти корни

соответствующего квадратного уравнения;
Слайд 9Графический способ
3). Построить эскиз графика и по нему
определить промежутки, на

которых
квадратичная функция принимает
положительные или отрицательные
значения
4). Выбрать нужный промежуток и записать ответ
Слайд 10Возможные случаи расположения параболы
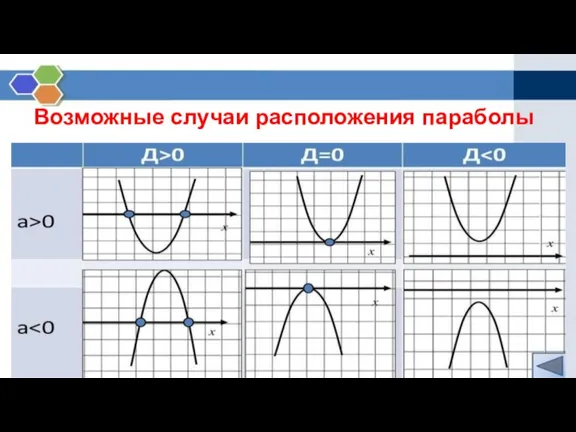
Слайд 11Например
Решить неравенство х²+5х-6≤0
Решение: 1). рассмотрим функцию
у = х²+5х-6,
это квадратичная

функция, графиком является парабола, т.к. а =1, то ветви направлены вверх.
Слайд 12
- 6
х
+
+
4). Запишем ответ:
(-∞; -6]U[1; +∞)
![- 6 х + + 4). Запишем ответ: (-∞; -6]U[1; +∞)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1142901/slide-11.jpg)
Слайд 13Решаем
1) х²-3х<0;
2) х²- 4х>0;
3) х²+2х ≥ 0;
4) -2х²+х+1 ≤ 0





![2) -6 1 х 3) Запишем ответ: (-∞; -6]U[1; +∞) 0 +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1142901/slide-5.jpg)





![- 6 х + + 4). Запишем ответ: (-∞; -6]U[1; +∞)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1142901/slide-11.jpg)

 Уравнение как способ перевода условия задачи на математический язык
Уравнение как способ перевода условия задачи на математический язык Длина окружности. Площадь круга
Длина окружности. Площадь круга Корень n-ой степени
Корень n-ой степени Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Стереометрия в задачах ЕГЭ
Стереометрия в задачах ЕГЭ Методы прогнозирования потерь в осевых турбинах
Методы прогнозирования потерь в осевых турбинах Прямая. Ортогональные проекции прямой линии
Прямая. Ортогональные проекции прямой линии Измерение длины отрезка
Измерение длины отрезка Случайные величины
Случайные величины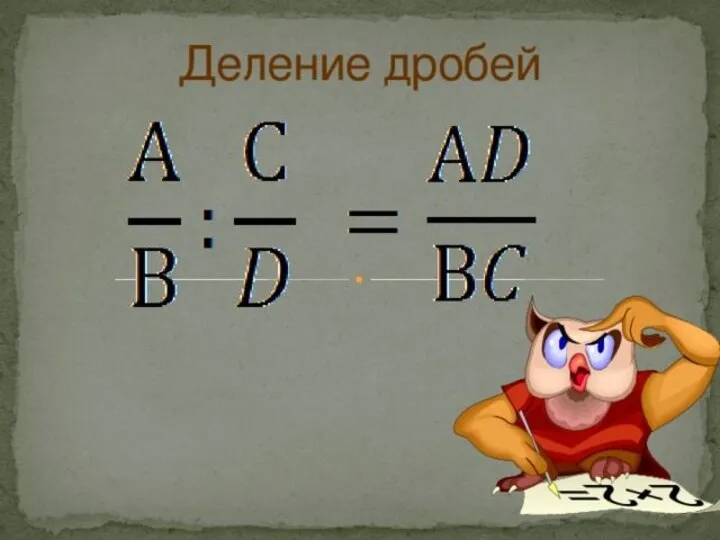 Деление дробей
Деление дробей Тест. Свойство простейших фигур
Тест. Свойство простейших фигур Многогранник с двумя основаниями
Многогранник с двумя основаниями Вычисление пределов функций
Вычисление пределов функций 20120818_pryamaya_i_obratnaya_proporcionalnost
20120818_pryamaya_i_obratnaya_proporcionalnost Расчетное задание
Расчетное задание Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Презентация на тему Решение задач различными способами
Презентация на тему Решение задач различными способами  Первообразная. 11 класс
Первообразная. 11 класс Анализ работы.12 задач
Анализ работы.12 задач Задачи на построение
Задачи на построение Векторы
Векторы Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Раз, два, три. Спортивно-математический турнир
Раз, два, три. Спортивно-математический турнир Применение синуса и косинуса при программировании движения с поворотом. Для учащихся 7-8 классов
Применение синуса и косинуса при программировании движения с поворотом. Для учащихся 7-8 классов Деление на 2
Деление на 2 Решение комбинаторных задач
Решение комбинаторных задач Лабораторно-практическая работа в парах
Лабораторно-практическая работа в парах Решение уравнений «В мире звезд»
Решение уравнений «В мире звезд»