Понятие и виды средних величин

ПЛАН ЗАНЯТИЯ

«НАДЕЖНЕЕ ФАКТОВ
РАЗВЕ ЧТО ЦИФРЫ»
Джордж Каннинг

ЦЕЛИ ЗАНЯТИЯ
Изучить понятие средней величины и виды средних величин
Развить умение применять исчисление средних показателей для основных экономических показателей страховой организации
Развить умение правильно обобщать, сравнивать, и анализировать статистические данные
Расширить общеобразовательный кругозор

СТАЛКИВАЛИСЬ ЛИ ВЫ В ПОВСЕДНЕВНОЙ ЖИЗНИ ИЛИ В ПРОФЕССИОНАЛЬНОЙ СРЕДЕ СО СРЕДНИМИ ЗНАЧЕНИЯМИ КАКИХ-ЛИБО ПОКАЗАТЕЛЕЙ?

ВИДЫ СРЕДНИХ ВЕЛИЧИН

ВИДЫ СРЕДНЕЙ АРФИМЕТИЧЕСКОЙ ВЕЛИЧИНЫ

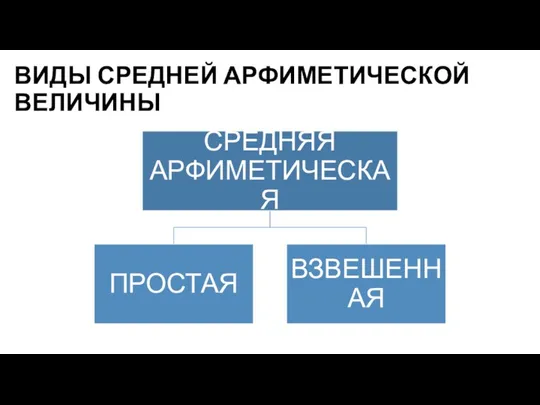
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ПРОСТАЯ
Простой средней арифметической величиной называется такое значение признака в расчете на единицу совокупности, при вычислении которого общий объем признака в совокупности сохраняется неизменным
ФОРМУЛА:

ПРИМЕР 1
За II полугодие 2015 года страховой агент Иванов И.И. получил следующую заработную плату (см. Таблицу 1). Рассчитайте среднюю заработную плату Иванова И.И. за II полугодие 2015 года.
Таблица 1
Решение: СР.з.п. = (24 000 + 32 000 + 18 000 + 26 000 + 28 000 + 34 000) = 27 000 рублей
6

СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЗВЕШЕННАЯ
Взвешенная средняя арифметическая — равна отношению суммы произведения значения признака на частоту повторения данного признака к сумме частот всех признаков. Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.
ФОРМУЛА:

ПРИМЕР 2
Найдите среднюю заработную плату одного страхового агента.
Таблица 2
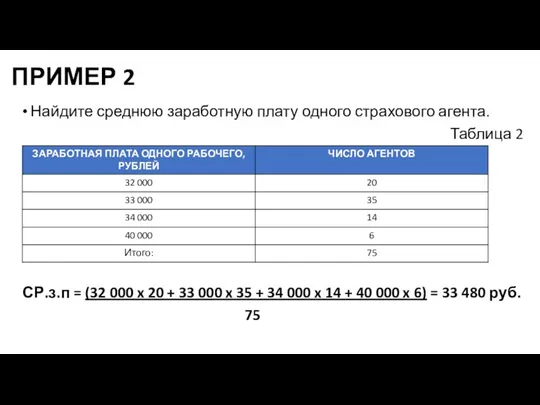
СР.з.п = (32 000 x 20 + 33 000 x 35 + 34 000 x 14 + 40 000 x 6) = 33 480 руб.
75

СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ВЕЛИЧИНА
Средняя квадратическая используется при вычислении средних величин, в расчете которых присутствует вторая степень числа (диаметр колеса, стороны геометрических фигур, вариативность какого-либо признака и т.д.)
ФОРМУЛА:

СМЫСЛ СРЕДНЕЙ КВАДРАТИЧЕСКОЙ
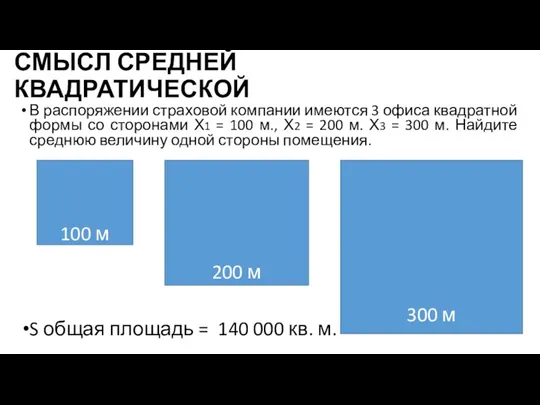
В распоряжении страховой компании имеются 3 офиса квадратной формы со сторонами Х1 = 100 м., Х2 = 200 м. Х3 = 300 м. Найдите среднюю величину одной стороны помещения.
S общая площадь = 140 000 кв. м.
100 м
200 м
300 м

ИТОГ РАЧЕТОВ

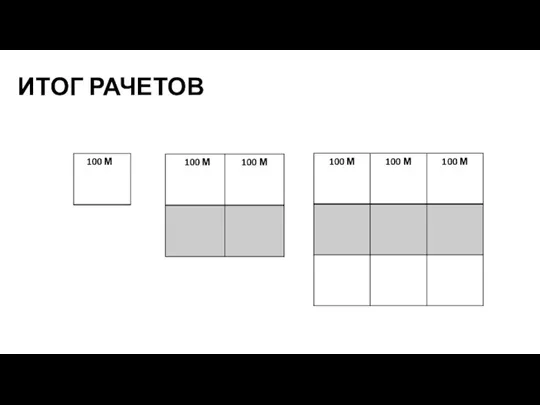
ИТОГ РАЧЕТОВ
Для того, чтобы найти среднюю величину одной стороны помещения, необходимо общую площадь разбить на три равных квадрата с одинаковой стороной. Длина этой стороны и будет искомой величиной.

ИТОГ РАСЧЕТОВ
S площадь всех квадратов = 140 000 кв. м.
?
?
?

РАСЧЕТЫ
ЕСЛИ РАСЧЕТ ПРОИЗВЕДЕН ПРИ ПОМОЩИ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ ПРОСТОЙ:
(100 + 200 + 300 ) : 3 = 200 метров
В таком случае S общая площадь = (200 x 200 ) x 3 = 120 000 кв. м.
200 м
200 м
200 м

РАСЧЕТЫ
216 м
216 м
216 м

СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
Если по условиям задачи необходимо, чтобы при осреднении неизменной оставалась сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней.
ФОРМУЛА:

ПРИМЕР 3
Автомобиль ехал из пункта А в пункт Б – со скоростью 60 км/час, а обратно из пункта Б в пункт А – 40 км/час. Найдите среднюю скорость автомобиля.
А 60 км/час Б
96 километров
40 км/час
При расчете необходимо, чтобы неизменной величиной оставалось время, затраченное на ОБЕ ПОЕЗДКИ, иначе средняя скорость может оказаться любой – от скорости черепахи до скорости света.

РАСЧЕТ

ВЫЧИСЛЕНИЕ СРЕДНИХ ВЕЛИЧИН
ОСНОВНЫХ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
СТРАХОВОЙ ОРГАНИЗАЦИИ

КАКИЕ ЭКОНОМИЧЕСКИЕ ПОКАЗАТЕЛИ ДЕЯТЕЛЬНОСТИ СТРАХОВЫХ ОРГАНИЗАЦИЙ ВЫ ЗНАЕТЕ?

ОСНОВНЫЕ ЭКОНОМИЧЕСКИЕ ПОКАЗАТЕЛИ ДЕЯТЕЛЬНОСТИ СТРАХОВЫХ ОРГАНИЗАЦИЙ
ОБЪЕМ СТРАХОВЫХ ПРЕМИЙ
ОБЪЕМ СТРАХОВЫХ ВЫПЛАТ
ОБЪЕМ ЧИСТОЙ ПРИБЫЛИ
РАЗМЕР КОМИССИОННОГО ВОЗНАГРАЖДЕНИЯ
РАЗМЕР ЗАРАБОТНОЙ ПЛАТЫ
РАЗМЕР СТРАХОВЫХ РЕЗЕРВОВ
РАЗМЕР ТЕХНИЧЕСКОГО РЕЗУЛЬТАТА

ЗАДАЧА 1
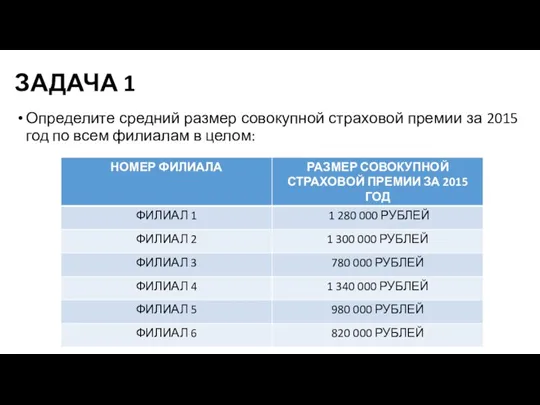
Определите средний размер совокупной страховой премии за 2015 год по всем филиалам в целом: