Презентация на тему Первый признак подобия треугольников

Цель:
Повторить определение подобных треугольников, теорему об отношении площадей подобных треугольников
Рассмотреть первый признак подобия треугольников, применение его при решении задач

Это фигуры, которые имеют одинаковую форму.
Подобные фигуры

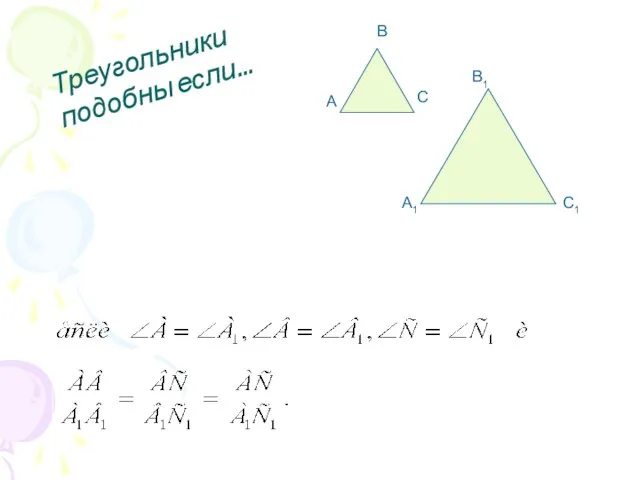
А
В
С
А1
В1
С1
Треугольники подобны если…

Устная работа.
1). Что такое сходственные стороны треугольников
2). Что такое коэффициент подобия?
3). Сформулировать теорему об отношении площадей подобных треугольников.

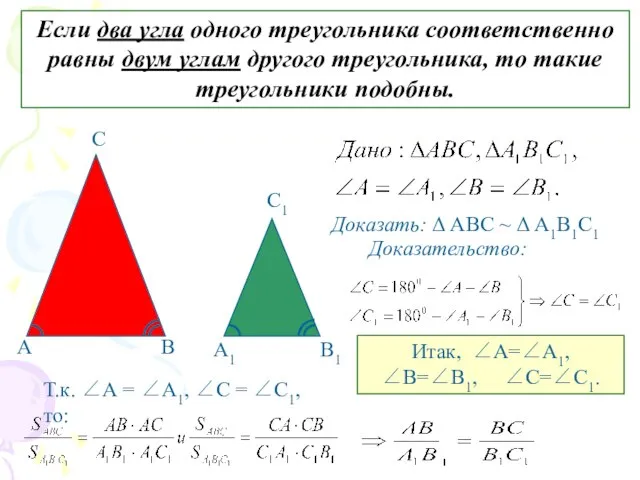
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
А
В
С
А1
В1
С1
Доказать: Δ АВС ~ Δ А1В1С1
Доказательство:
Т.к. ∠А = ∠А1, ∠С = ∠С1, то:
Итак, ∠А=∠А1, ∠В=∠В1, ∠С=∠С1.

2. Формулировка и доказательство теоремы

Т.к. ∠А = ∠А1, ∠В = ∠В1, то
Δ АВС ~ Δ А1В1С1

3. Решение задач на применение признака подобия треугольников

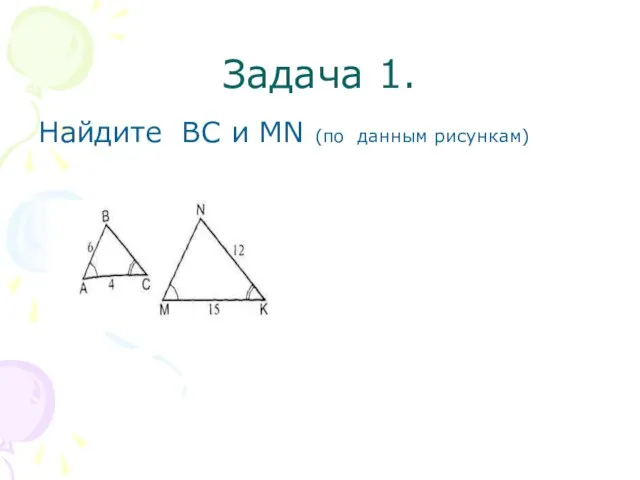
Задача 1.
Найдите ВС и МN (по данным рисункам)

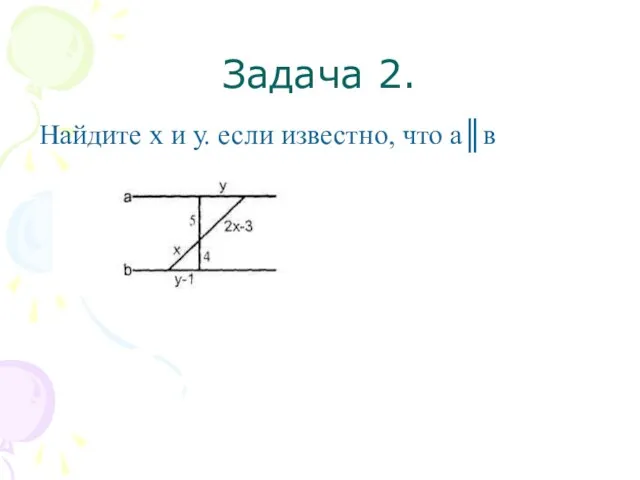
Задача 2.
Найдите х и у. если известно, что а║в

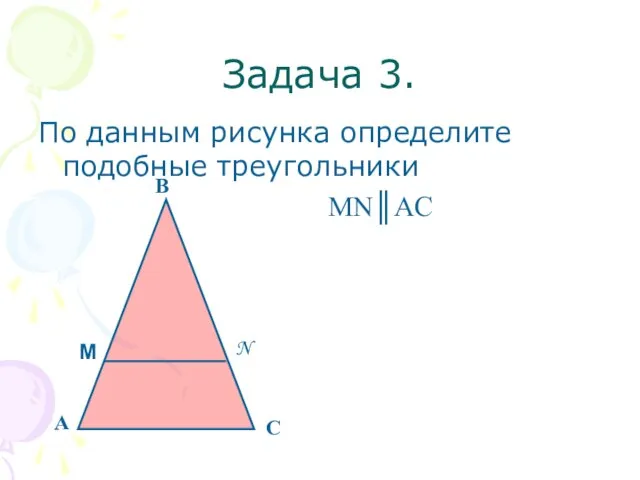
Задача 3.
По данным рисунка определите подобные треугольники
MN║AC
А
В
С
М
N

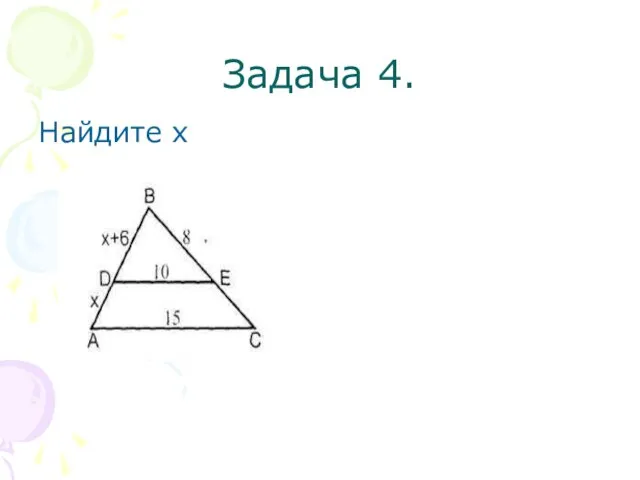
Задача 4.
Найдите х

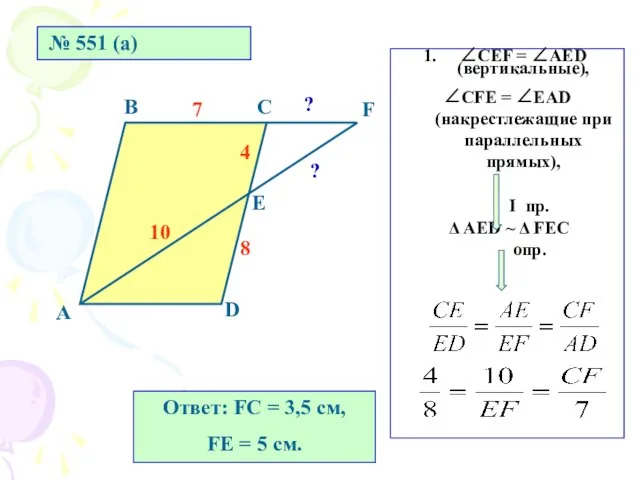
№ 551 (а)
А
В
С
D
Е
F
8
4
7
10
?
?
∠СЕF = ∠AED (вертикальные),
∠СFE = ∠EAD (накрестлежащие при параллельных прямых),
I пр.
Δ АЕD ~ Δ FЕС
опр.
Ответ: FC = 3,5 см,
FЕ = 5 см.