РўР’РёРњРЎ_Лекция 5_Непрерывные СЃРучайные РІРµРичины

Пролог
Лекция 5. Непрерывные случайные величины
В качестве исчерпывающего описания дискретной случайной величины обычно рассматривается закон её распределения: ряд распределения или формула, позволяющая находить вероятности любых значений случайной величины. Этот способ не является единственным и, главное, не является универсальным. Он не применим к случайным величинам множество значений которых бесконечно и не является счётным.
Возможен другой подход к описанию случайных величин: рассматривать не вероятности событий X=x для возможных значений x, а вероятности событий X

Определение 1. Функцией распределения случайной величины X называется функция F(x), которая для каждого значения x определяет вероятность того, что случайная величина X принимает значение меньше чем x, т.е.
Геометрически это означает, что случайная точка X попадёт левее заданной точки x.
Функцию распределения называют также интегральной функцией распределения.
§1. Функция распределения СВ
Лекция 5. Непрерывные случайные величины

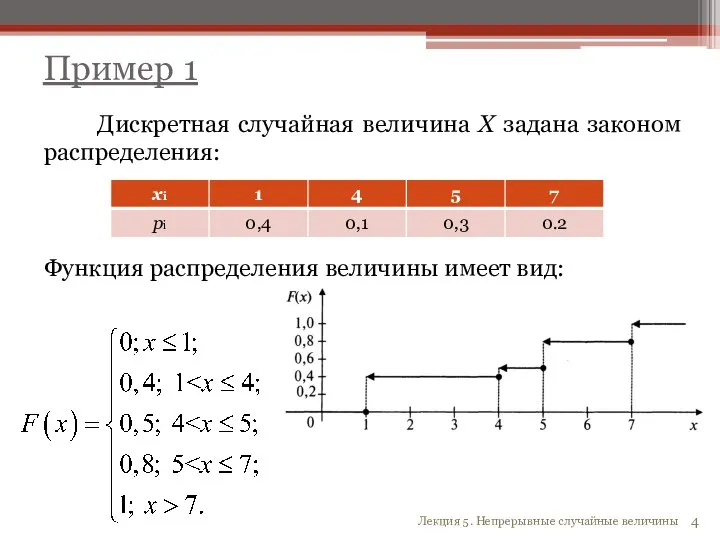
Пример 1
Лекция 5. Непрерывные случайные величины
Дискретная случайная величина X задана законом распределения:
Функция распределения величины имеет вид:

Свойства функции распределения.
1. Функция распределения принимает неотрицательные значения, заключённые между нулём и единицей:
Утверждение вытекает из определения функции распределения как вероятности (1).
§1. Функция распределения СВ
Лекция 5. Непрерывные случайные величины

Свойства функции распределения.
2. Функция распределения есть неубывающая функция на всей числовой прямой:
Утверждение вытекает из теоремы о вероятности суммы несовместных событий:
§1. Функция распределения СВ
Лекция 5. Непрерывные случайные величины

Свойства функции распределения.
3. Функция распределения на границах области определения принимает свои наименьшее и наибольшее значения:
Утверждение вытекает определения вероятности:
§1. Функция распределения СВ
Лекция 5. Непрерывные случайные величины

Свойства функции распределения.
4. Вероятность попадания случайной величины в интервал [х1,х2) равна приращению её функции распределения на этом интервале:
Утверждение было получено при доказательстве свойства 2:
§1. Функция распределения СВ
Лекция 5. Непрерывные случайные величины

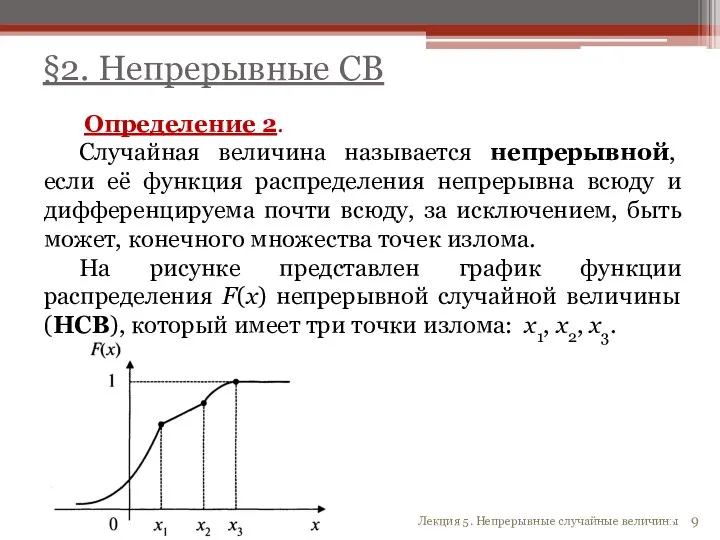
Определение 2.
Случайная величина называется непрерывной, если её функция распределения непрерывна всюду и дифференцируема почти всюду, за исключением, быть может, конечного множества точек излома.
На рисунке представлен график функции распределения F(x) непрерывной случайной величины (НСВ), который имеет три точки излома: х1, х2, х3.
§2. Непрерывные СВ
Лекция 5. Непрерывные случайные величины

Теорема 1. Вероятность отдельно взятого значения непрерывной случайной величины равна нулю.
Утверждение следует из свойств функции распределения случайной величины и свойства предела функции, непрерывной в точке:
Следствие. Вероятность попадание непрерывной случайной величины в интервал не зависит от принадлежности интервалу его концов:
§2. Непрерывные СВ
Лекция 5. Непрерывные случайные величины

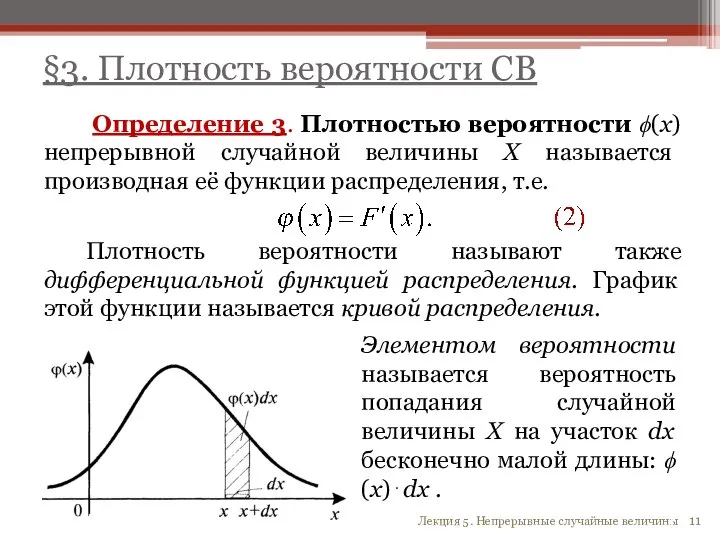
Определение 3. Плотностью вероятности ϕ(x) непрерывной случайной величины X называется производная её функции распределения, т.е.
Плотность вероятности называют также дифференциальной функцией распределения. График этой функции называется кривой распределения.
§3. Плотность вероятности СВ
Лекция 5. Непрерывные случайные величины
Элементом вероятности называется вероятность попадания случайной величины X на участок dx бесконечно малой длины: ϕ(x)⋅dx .

Пример 2
Лекция 5. Непрерывные случайные величины
Непрерывная случайная величина X задана функцией распределения:
Её плотность вероятности имеет вид:

Свойства плотности вероятности.
1. Плотность вероятности неотрицательная функция:
Утверждение следует из определения плотности вероятности как производной неубывающей функции (функции распределения).
§3. Плотность вероятности СВ
Лекция 5. Непрерывные случайные величины

Свойства плотности вероятности.
2. Вероятность попадания случайной величины в интервал [a, b] равна определённому интегралу от её плотности вероятности на этом интервале:
Утверждение следует из свойства 4 функции распределения; того факта, что функция распределения F(x) есть первообразная для плотности вероятности ϕ(x) и формулы Ньютона-Лейбница:
§3. Плотность вероятности СВ
Лекция 5. Непрерывные случайные величины

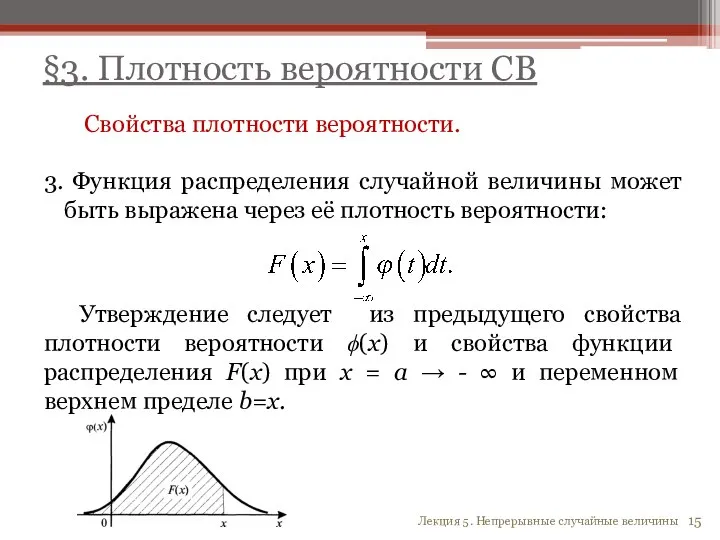
Свойства плотности вероятности.
3. Функция распределения случайной величины может быть выражена через её плотность вероятности:
Утверждение следует из предыдущего свойства плотности вероятности ϕ(x) и свойства функции распределения F(x) при x = a → - ∞ и переменном верхнем пределе b=x.
§3. Плотность вероятности СВ
Лекция 5. Непрерывные случайные величины

Свойства плотности вероятности.
4. Несобственный интеграл по всей числовой прямой от плотности вероятности равен единице:
Утверждение следует из предыдущего свойства плотности вероятности и свойства функции распределения: F(+∞)=1.
С геометрической точки зрения свойство означает, что площадь фигуры под всей кривой распределения равна единице.
§3. Плотность вероятности СВ
Лекция 5. Непрерывные случайные величины

§4. Равномерное распределение
Определение 5.
НСВ имеет равномерное распределение на отрезке [a, b], если её плотность вероятности ϕ(х) постоянна на этом отрезке и равна нулю вне его:
График плотности вероятности имеет вид:
Лекция 5. Непрерывные случайные величины

§4. Равномерное распределение
Теорема 2.
Функция распределения НСВ, имеющей равномерное распределение на отрезке [a, b], имеет вид:
График функции распределения имеет вид:
Лекция 5. Непрерывные случайные величины

§4. Равномерное распределение
Доказательство.
При x ≤ a функция распределения F(x)=0.
При a < x ≤ b функция распределения равна:
При x > b функция распределения равна:
Лекция 5. Непрерывные случайные величины

Пример 3
Лекция 5. Непрерывные случайные величины
Эксперимент: выбрать наугад время прихода пассажира на остановку в диапазоне [0; 2].
(Диапазон определяется графиком регулярного (равномерного) движения транспорта).
Событие A: время ожидания пассажиром автобуса составит не больше полминуты.
Величина Х: время ожидания пассажиром автобуса.

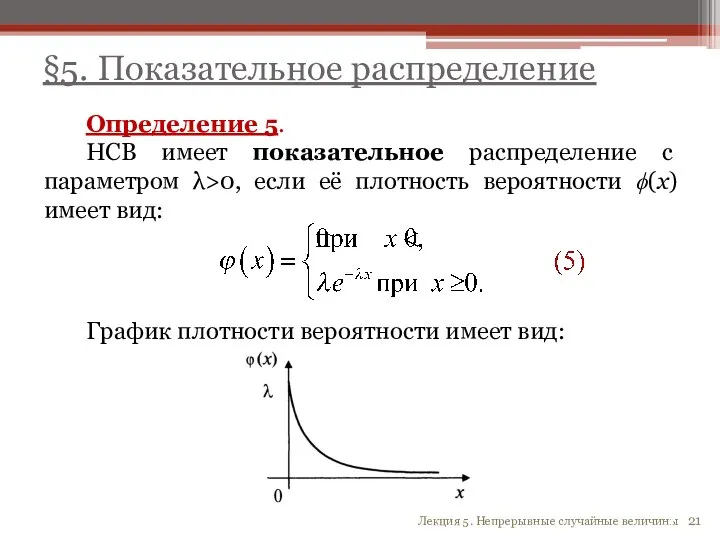
§5. Показательное распределение
Определение 5.
НСВ имеет показательное распределение с параметром λ>0, если её плотность вероятности ϕ(х) имеет вид:
График плотности вероятности имеет вид:
Лекция 5. Непрерывные случайные величины

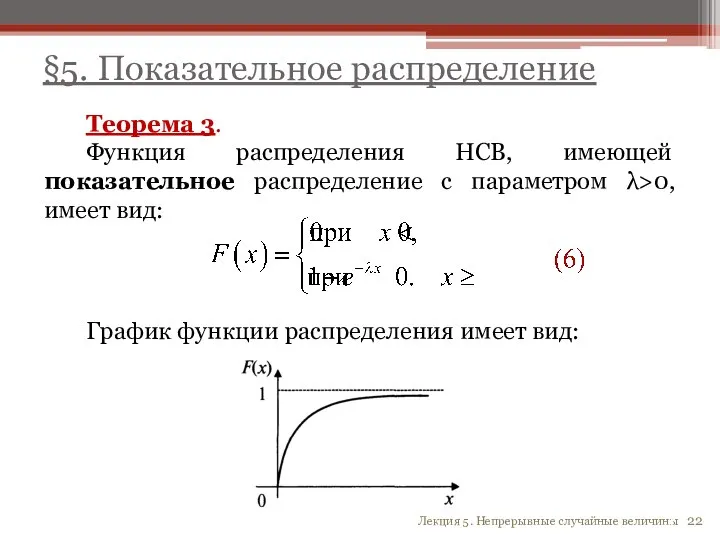
§5. Показательное распределение
Теорема 3.
Функция распределения НСВ, имеющей показательное распределение с параметром λ>0, имеет вид:
График функции распределения имеет вид:
Лекция 5. Непрерывные случайные величины

§5. Показательное распределение
Доказательство.
При x < 0 функция распределения F(x)=0.
При x ≥ b функция распределения равна:
Замечание.
Показательный закон распределения играет важную роль в теории массового обслуживания. Так, например, интервал времени между соседними событиями в простейшем потоке событий имеет показательное распределение с параметром λ – интенсивностью потока.
Лекция 5. Непрерывные случайные величины

§6. Нормальное распределение
Определение 6.
НСВ имеет нормальное распределение с параметрами a и σ2, если её плотность вероятности ϕN(х) имеет вид:
Замечание.
Нормальный закон распределения наиболее часто встречается на практике. Он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Лекция 5. Непрерывные случайные величины

§6. Нормальное распределение
График плотности вероятности нормально распределённой случайной величины с параметрами a и σ2, т.е. Х ~ N(a,σ2), называют гауссовой или нормальной кривой.
Нормальная кривая имеет:
ось симметрии: прямую х = а,
точку максимума: точку х = а,
максимум:
две точки перегиба:
Лекция 5. Непрерывные случайные величины

§6. Нормальное распределение
Теорема 4.
Функция распределения НСВ, имеющей нормальное распределение с параметрами a и σ2 имеет вид:
где - функция Лапласа.
График функции распределения имеет вид:
Лекция 5. Непрерывные случайные величины

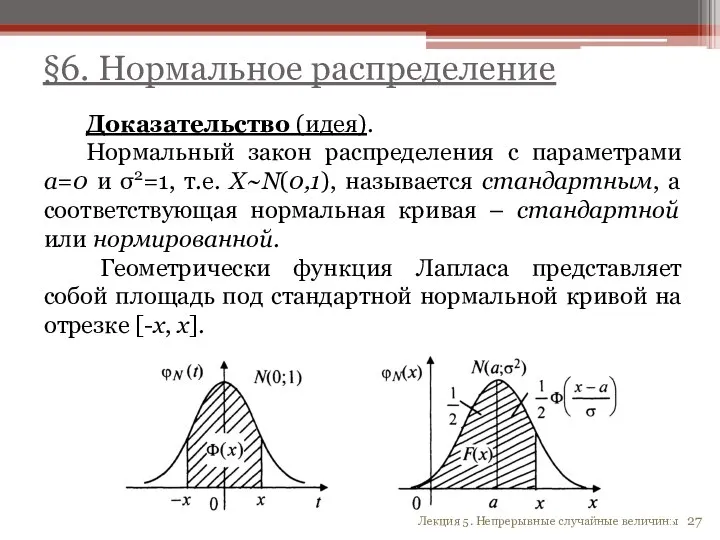
§6. Нормальное распределение
Доказательство (идея).
Нормальный закон распределения с параметрами a=0 и σ2=1, т.е. Х~N(0,1), называется стандартным, а соответствующая нормальная кривая – стандартной или нормированной.
Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-х, х].
Лекция 5. Непрерывные случайные величины

Свойства нормального распределения.
1. Вероятность попадания случайной величины в интервал [x1, x2] равна:
где
Утверждение следует из свойства функции распределения:
§6. Нормальное распределение
Лекция 5. Непрерывные случайные величины

Свойства нормального распределения.
2. Вероятность отклонения значений случайной величины от значения параметра а (по абсолютной величине) не более чем на δ равна:
где
Утверждение следует из предыдущего свойства и нечётности функции Лапласа:
§6. Нормальное распределение
Лекция 5. Непрерывные случайные величины

Свойства нормального распределения.
3. «Правило трёх сигм». Практически достоверно, что значение случайной величины заключено в интервале [a - 3σ; a + 3σ].
Утверждение следует из предыдущего свойства и таблицы значений функции Лапласа.
§6. Нормальное распределение
Лекция 5. Непрерывные случайные величины