Слайд 2Задание №1
1 - измерить углы различных треугольников, найти сумму всех углов, сделать

вывод
2 - измерить углы различных четырёхугольников, найти сумму всех углов, сделать вывод
3 - измерить углы различных пятиугольников, найти сумму всех углов, сделать вывод
4 - измерить углы различных шестиугольников найти сумму всех углов, сделать вывод
Слайд 3Выводы
Сумма углов любого треугольника равна 180°
Сумма углов любого четырёхугольника = 360°
Сумма углов
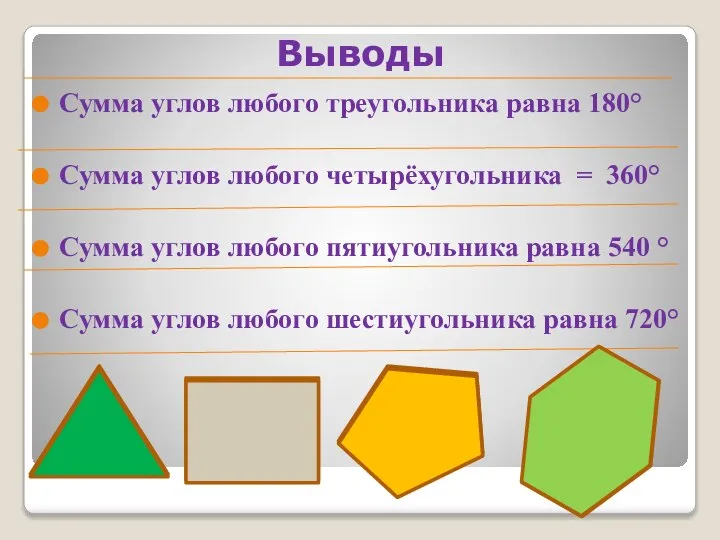
любого пятиугольника равна 540 °
Сумма углов любого шестиугольника равна 720°
Слайд 4Найти сумму углов 12-тиугольника
Необходима формула. Находим закономерность. Свяжем все результаты измерения со
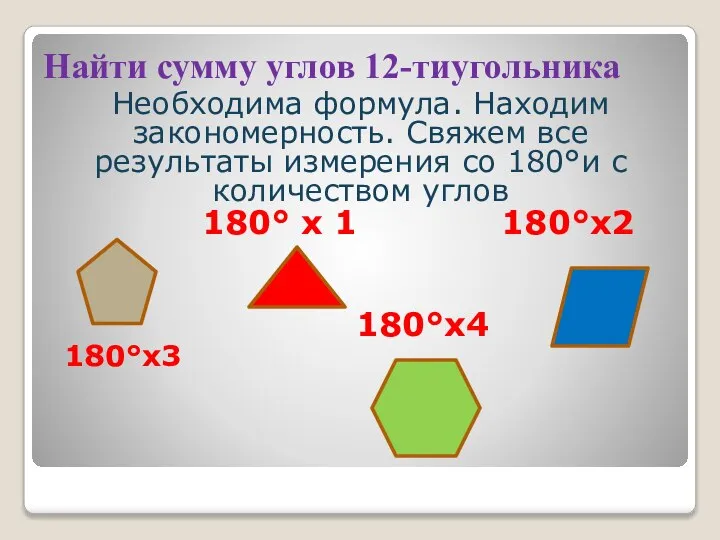
180°и с количеством углов
180° х 1 180°х2
180°х4
180°х3
Слайд 5Найти сумму углов 12-тиугольника
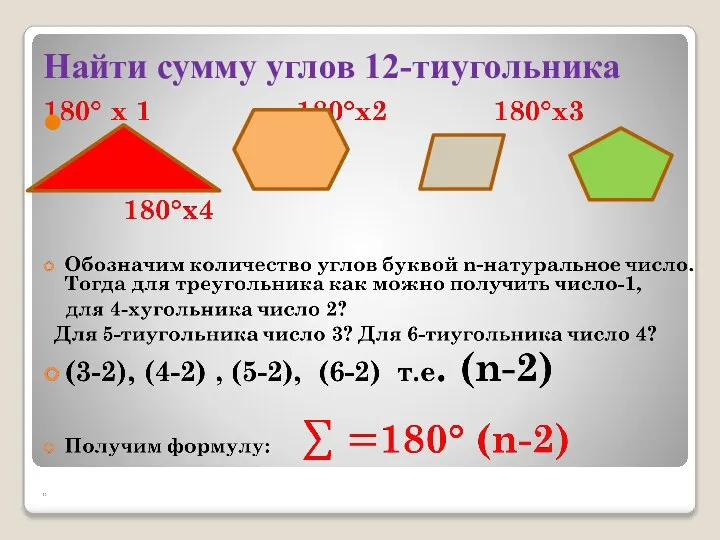
Слайд 6Найти сумму углов 12-тиугольника
Решение:
Подставляем в формулу вместо n число, обозначающее количество углов

, т.е. 12, получим:
∑=180°(12-2)=180°х 10= 1800 °
Слайд 7Задание №2
1 - Провести диагонали в различных треугольниках, подсчитать их количество;
2 -

Провести диагонали в различных
четырёхугольниках, подсчитать их количество;
3 - Провести диагонали в различных пятиугольниках, подсчитать их количество;
4 -Провести диагонали в различных шестиугольниках, подсчитать их количество.
Слайд 8Результаты опытов
Треугольник- нет диагоналей
Четырёхугольник -2
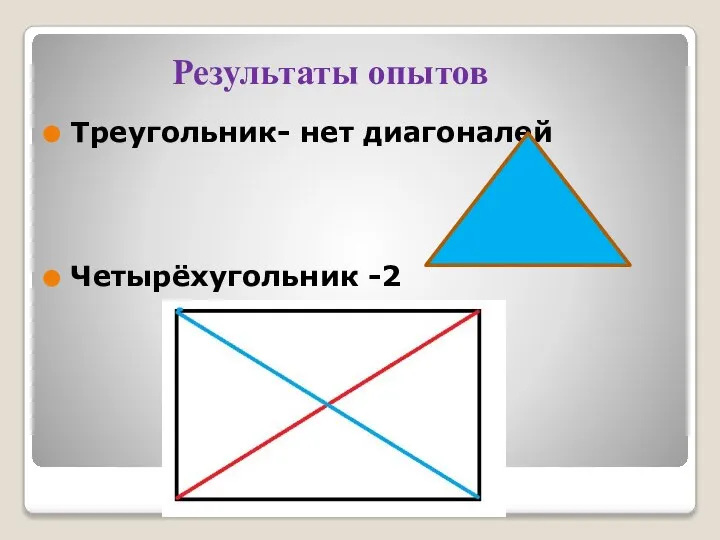
Слайд 9
Пятиугольник-5
Шестиугольник-9
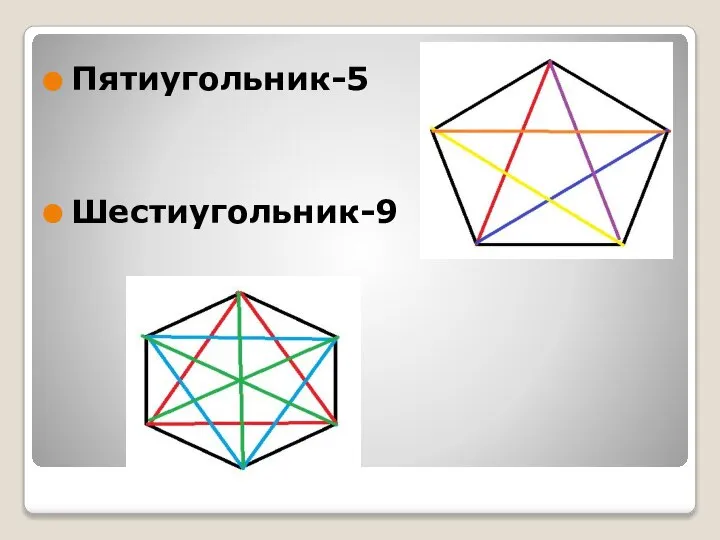
Слайд 10(5-3)х5: 2=5 (6-3)х6:2=9 N =n·(n – 3):2
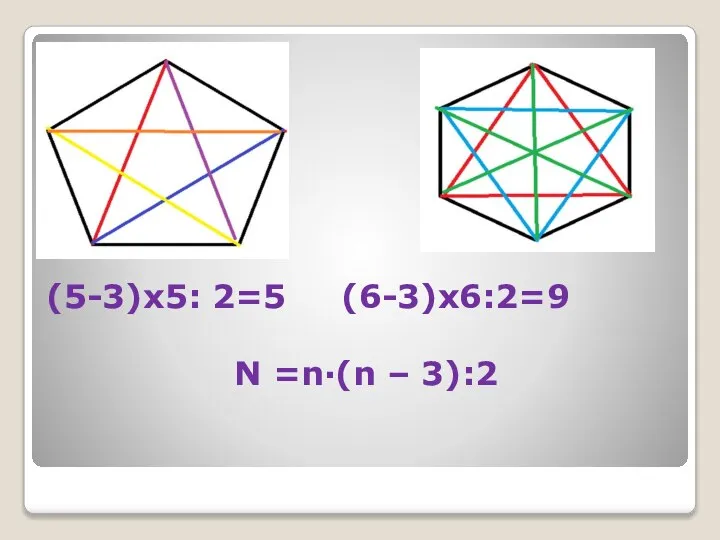
Слайд 11 Вот и весь секрет!
N =n·(n – 3):2
∑=180° (n-2)











 Математический маятник. Измерения
Математический маятник. Измерения Признаки равенства треугольников
Признаки равенства треугольников Пропорция
Пропорция Решение текстовых задач
Решение текстовых задач Цифра ноль
Цифра ноль Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Решение задач с помощью уравнений
Решение задач с помощью уравнений Число и цифра 5
Число и цифра 5 Презентация на тему Решение задач различными способами
Презентация на тему Решение задач различными способами  Число π. Длина окружности
Число π. Длина окружности Теория игр
Теория игр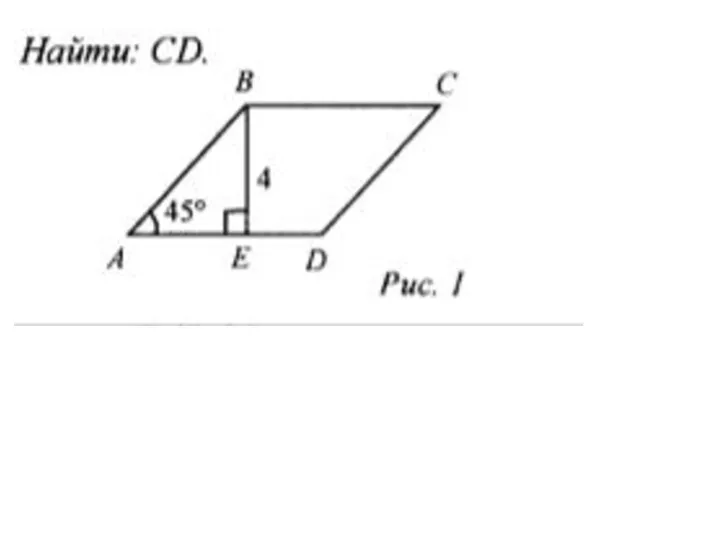 Вычисление площадей
Вычисление площадей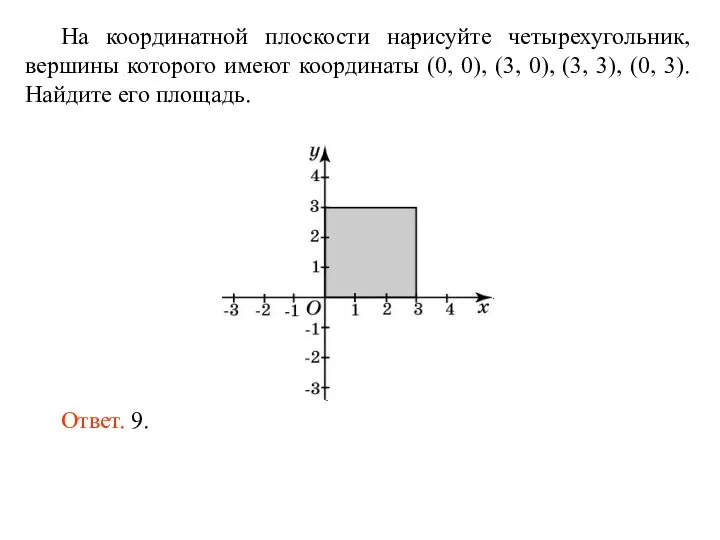 Площадь фигур на координатной плоскости
Площадь фигур на координатной плоскости Распределительная логистика. Практическое задание №8
Распределительная логистика. Практическое задание №8 Окружность. Методическая разработка урока
Окружность. Методическая разработка урока История дробей
История дробей Наибольшие и найменьшее значение функции
Наибольшие и найменьшее значение функции Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass Случаи вычитания 11-
Случаи вычитания 11- Функция. Свойства функции
Функция. Свойства функции Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Математика в профессиях
Математика в профессиях Симметрия
Симметрия Взятие Измаила в математических и исторических нюансах
Взятие Измаила в математических и исторических нюансах Векторы. Решение задач
Векторы. Решение задач Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс) Треугольник
Треугольник Четность, нечетность синуса, косинуса, тангенса, котангенса
Четность, нечетность синуса, косинуса, тангенса, котангенса