- Главная
- Математика
- Система однородных линейных уравнений

Содержание
Слайд 3Такая система всегда совместна, так как имеет, по крайней мере, нулевое решение.
Если
Такая система всегда совместна, так как имеет, по крайней мере, нулевое решение.
Если

в системе число неизвестных равно числу уравнений (n=m), а ее определитель не равен нулю, то такая система имеет только нулевое решение.
Для того, чтобы система имела ненулевое решение, необходимо, чтобы число уравнений было меньше числа переменных или чтобы определитель системы был равен нулю.
Для того, чтобы система имела ненулевое решение, необходимо, чтобы число уравнений было меньше числа переменных или чтобы определитель системы был равен нулю.
- Предыдущая
Моя семья. ФотоальбомСледующая -
Виды ожогов. ПМП при ожогах
 Природа России в цифрах и загадках
Природа России в цифрах и загадках Логарифм числа
Логарифм числа Задания по математике (5 класс, часть 8)
Задания по математике (5 класс, часть 8) Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Математика вокруг нас. Числа в загадках, пословицах и поговорках
Математика вокруг нас. Числа в загадках, пословицах и поговорках Длина. Сантиметр
Длина. Сантиметр Декартова прямоугольная система координат на плоскости
Декартова прямоугольная система координат на плоскости Элементы теории случайных процессов
Элементы теории случайных процессов Геометрическая оптика. 11 класс. ЕГЭ
Геометрическая оптика. 11 класс. ЕГЭ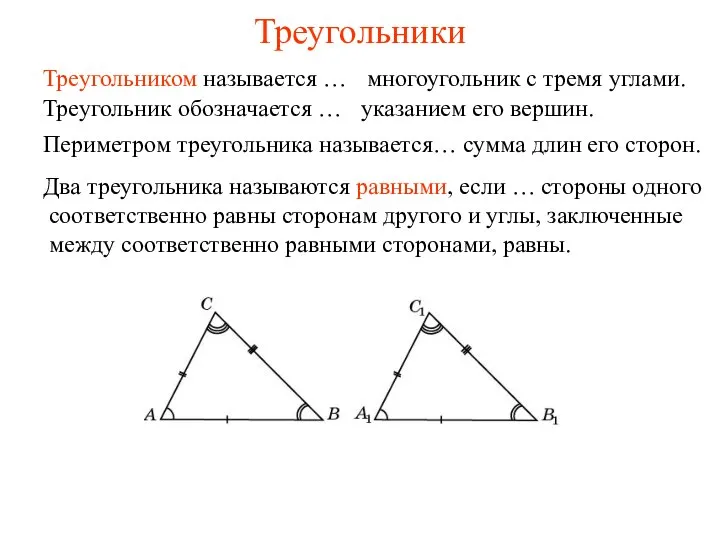 Треугольники
Треугольники К разговору о пропорциях
К разговору о пропорциях Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Ноль и нуль
Ноль и нуль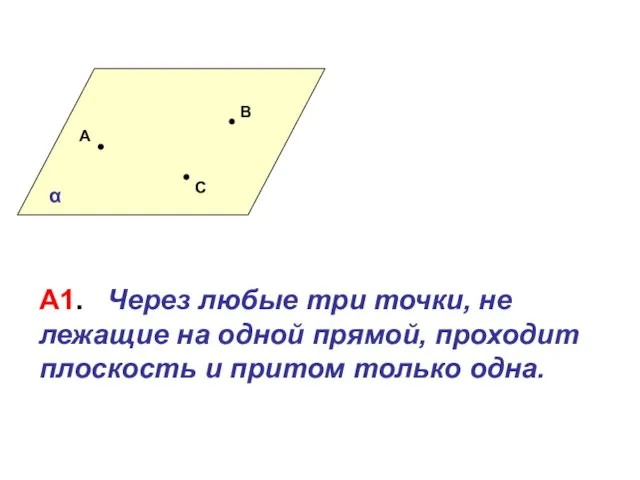 Плоскости
Плоскости Графики уравнений, содержащих модули
Графики уравнений, содержащих модули Решение задач
Решение задач Проценты (1)
Проценты (1) Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб
Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб Простейшие задачи в координатах
Простейшие задачи в координатах Дробно-рациональные уравнения
Дробно-рациональные уравнения Двугранные углы
Двугранные углы Лекция_05
Лекция_05 Нахождение числа по заданному значению его дроби
Нахождение числа по заданному значению его дроби Расстояние между точкой и прямой
Расстояние между точкой и прямой Пространство
Пространство Комбинаторика и вероятность
Комбинаторика и вероятность Сокращение дробей. Тождество
Сокращение дробей. Тождество Презентация на тему ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ
Презентация на тему ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ