Содержание
- 2. ЦЕЛИ УРОКА: ВВЕСТИ ПОНЯТИЕ ДВУГРАННОГО УГЛА И ЕГО ЛИНЕЙНОГО УГЛА; РАССМОТРЕТЬ ЗАДАЧИ НА ПРИМЕНЕНИЕ ЭТИХ ПОНЯТИЙ;
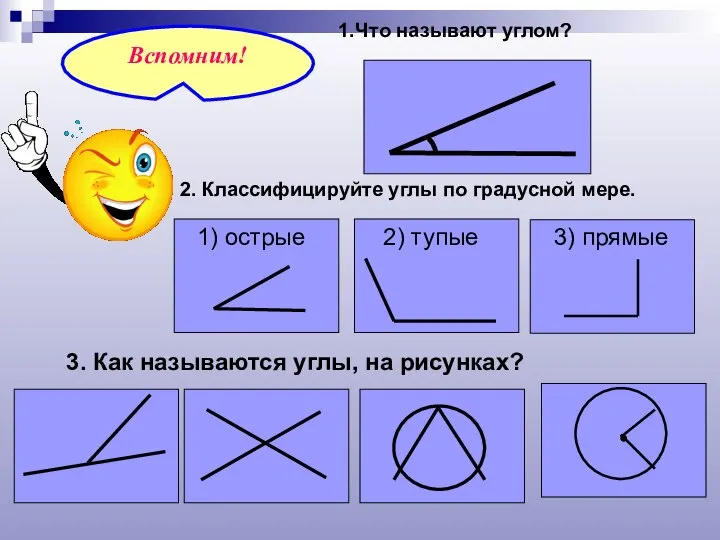
- 3. 1.Что называют углом? 2. Классифицируйте углы по градусной мере. 3. Как называются углы, на рисунках?
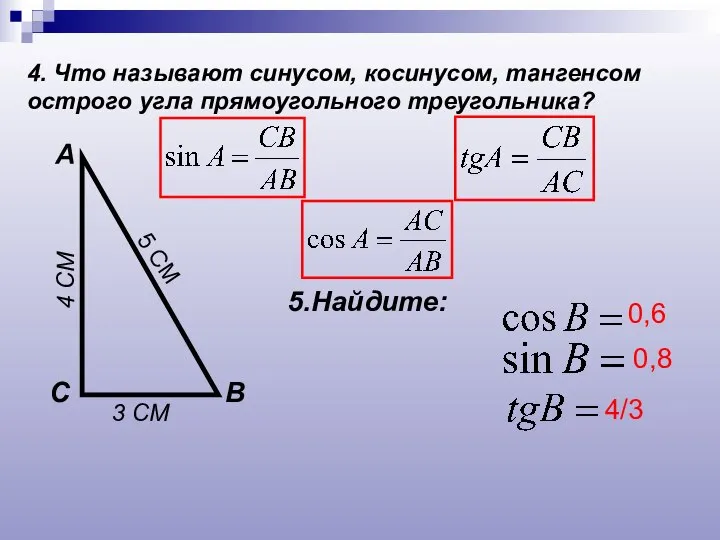
- 4. 4. Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника? А В С 5.Найдите: 3 СМ
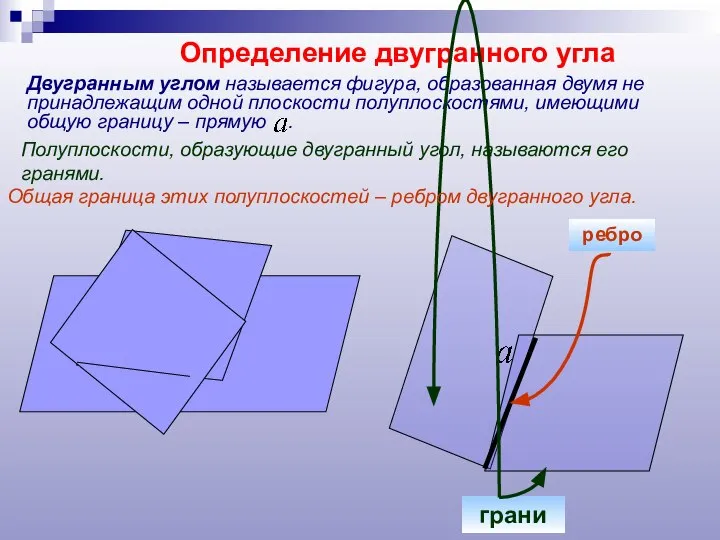
- 5. Определение двугранного угла Двугранным углом называется фигура, образованная двумя не принадлежащим одной плоскости полуплоскостями, имеющими общую
- 6. В обыденной жизни, форму двугранного угла имеют
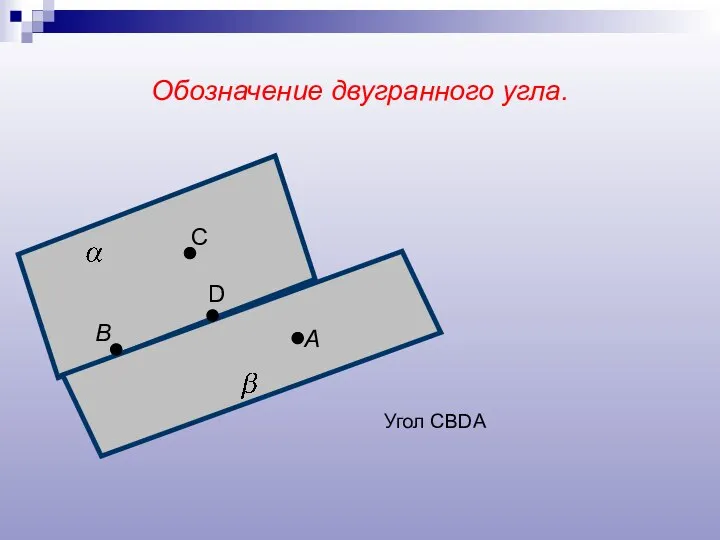
- 7. Обозначение двугранного угла. А В С D Угол CBDA
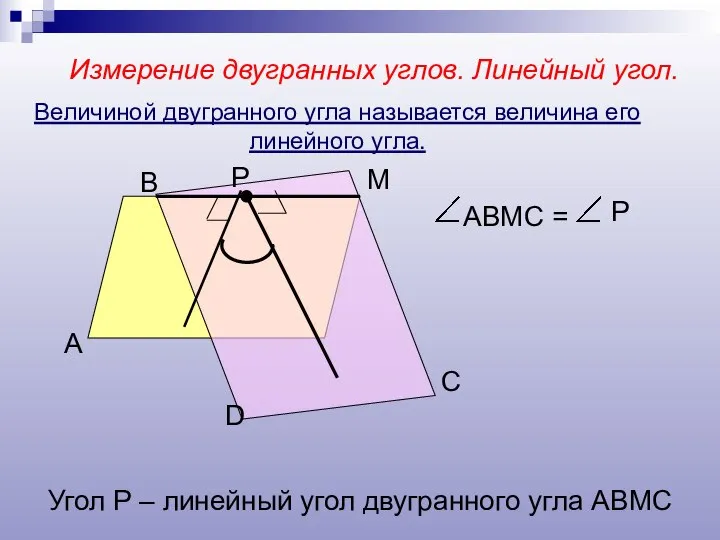
- 8. Измерение двугранных углов. Линейный угол. А В М D Р С АВМС = Р Угол Р
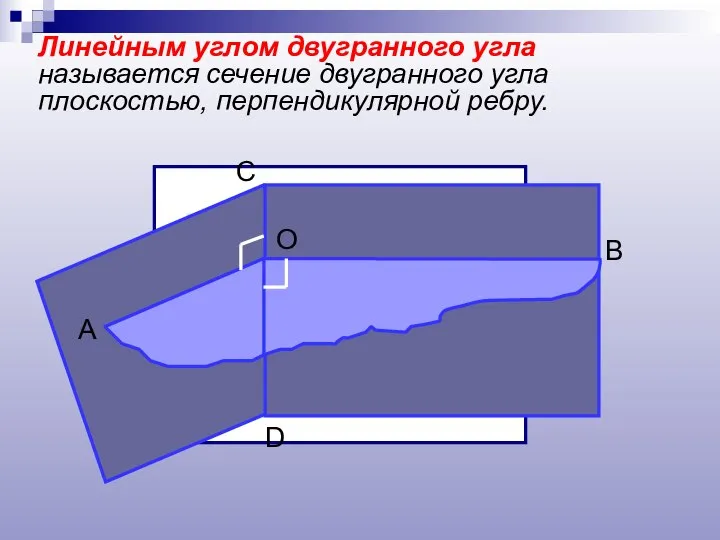
- 9. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
- 10. Способ нахождения (построения) линейного угла. 1. Найти ( увидеть) ребро и грани двугранного угла 2. В
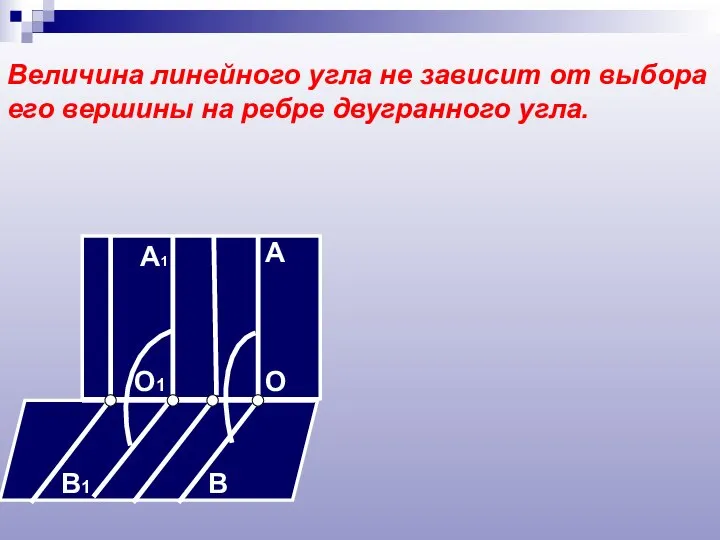
- 11. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. A B O
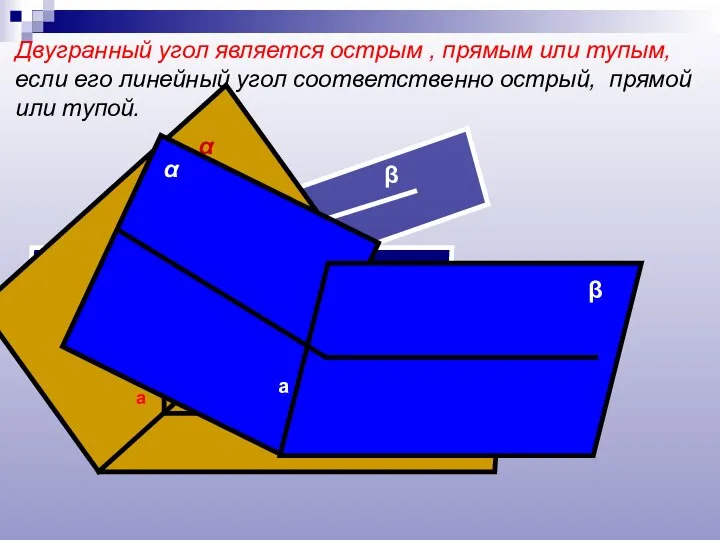
- 12. Двугранный угол является острым , прямым или тупым, если его линейный угол соответственно острый, прямой или
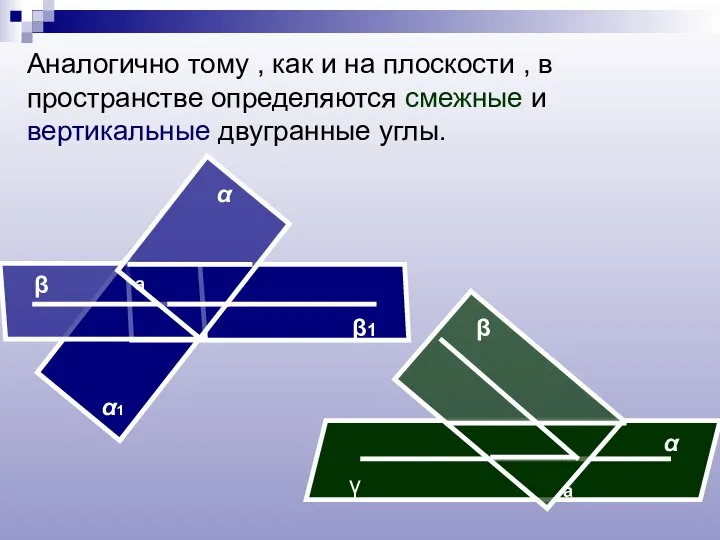
- 13. Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.
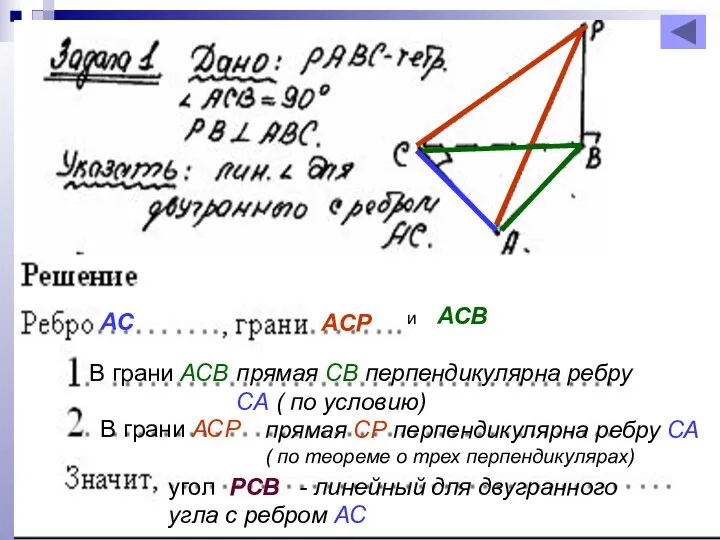
- 14. АС АСР и АСВ прямая СВ перпендикулярна ребру СА ( по условию) В грани АСВ В
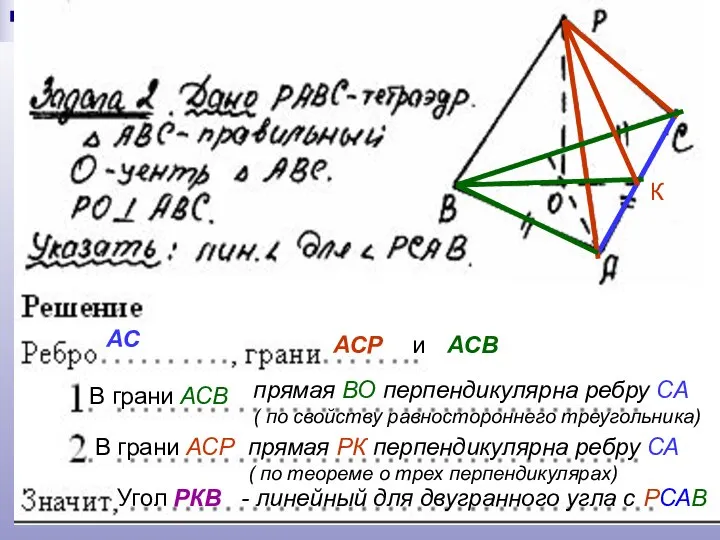
- 15. АС АСР и АСВ В грани АСВ прямая ВО перпендикулярна ребру СА ( по свойству равностороннего
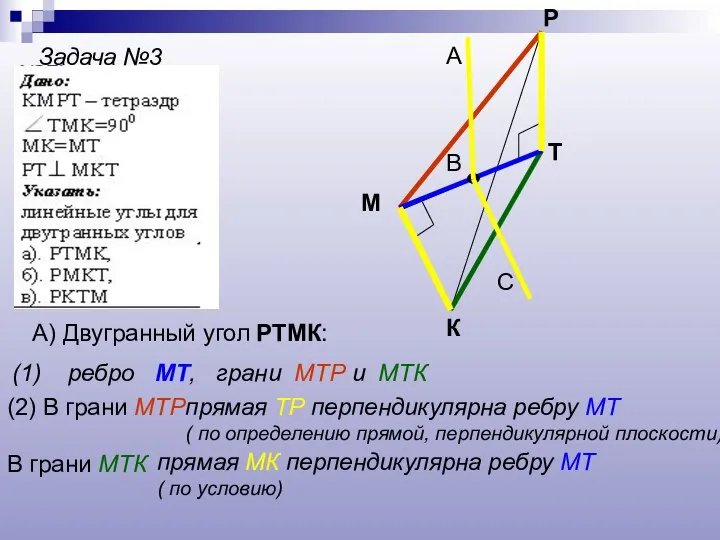
- 16. Задача №3 К М Р Т А) Двугранный угол РТМК: (1) ребро МТ, грани МТР и
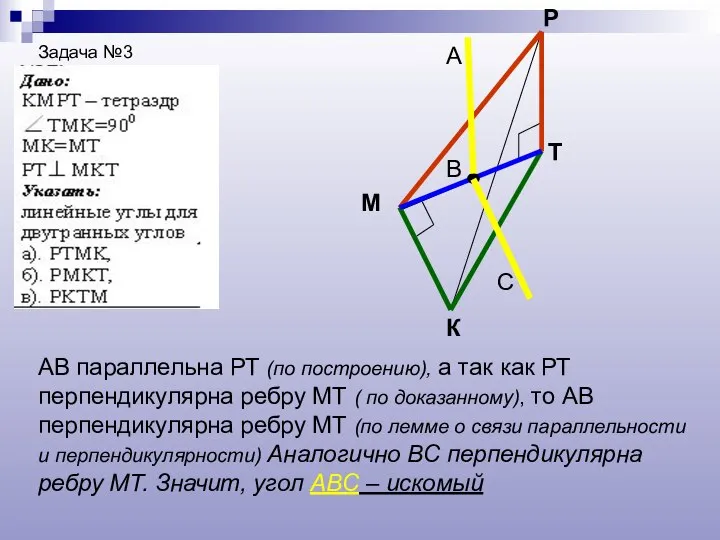
- 17. Задача №3 К М Р Т В А С АВ параллельна РТ (по построению), а так
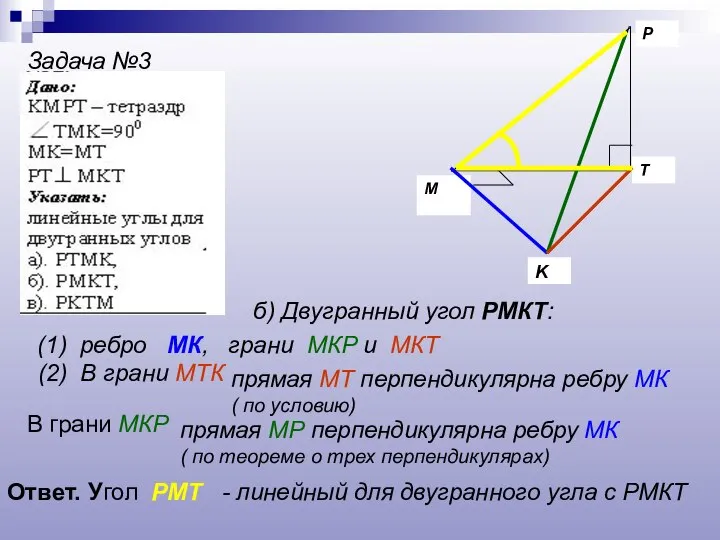
- 18. P K T M Задача №3 б) Двугранный угол РМКТ: (1) ребро МК, грани МКР и
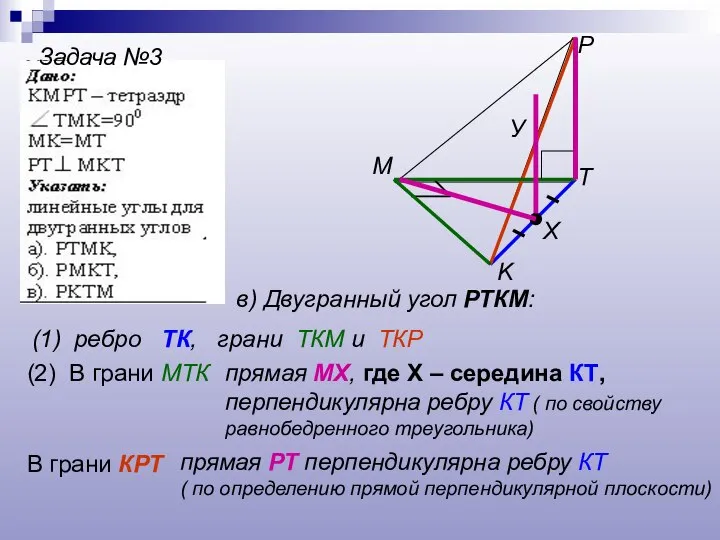
- 19. Задача №3 T K P M в) Двугранный угол РТКМ: (1) ребро ТК, грани ТКМ и
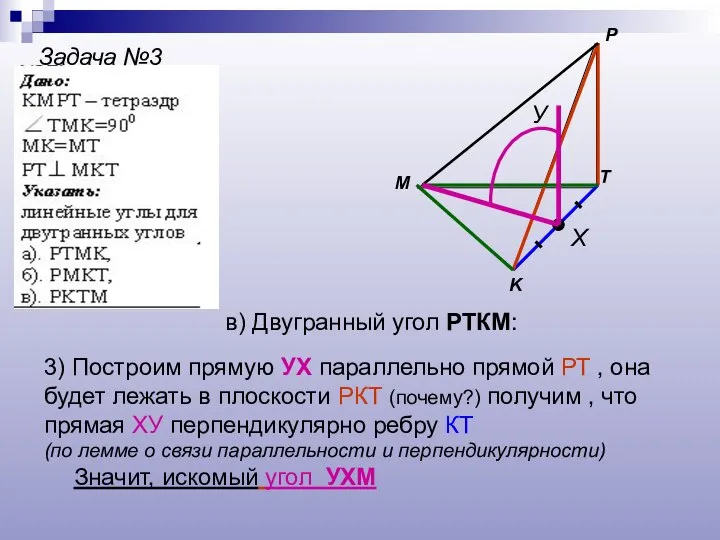
- 20. Задача №3 M P K T Х У в) Двугранный угол РТКМ: 3) Построим прямую УХ
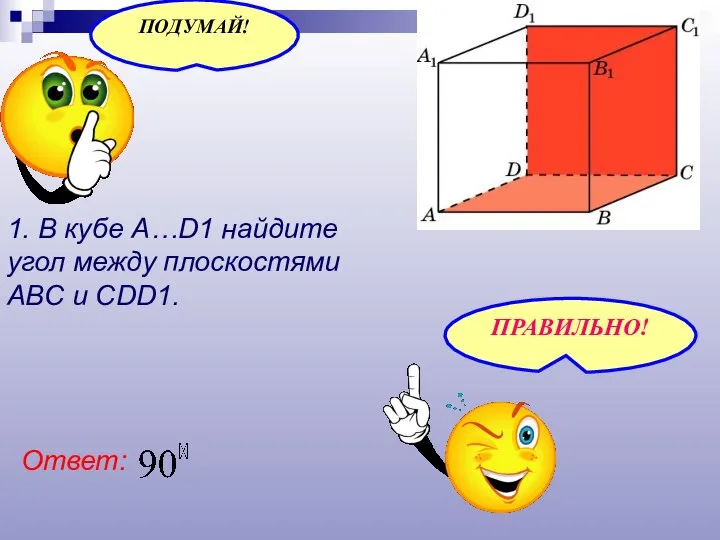
- 21. 1. В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ:
- 22. 2.В кубе A…D1 найдите угол между плоскостями ABC и CDA1. Ответ:
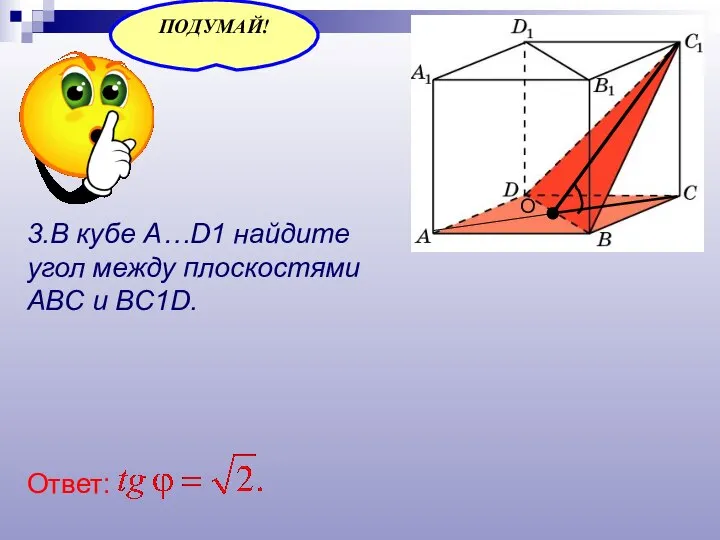
- 23. 3.В кубе A…D1 найдите угол между плоскостями ABC и BC1D. Ответ: О
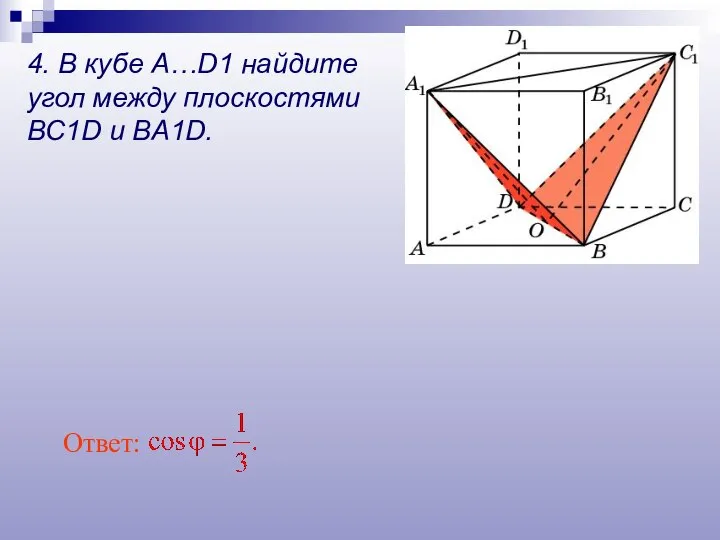
- 24. Ответ: 4. В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.
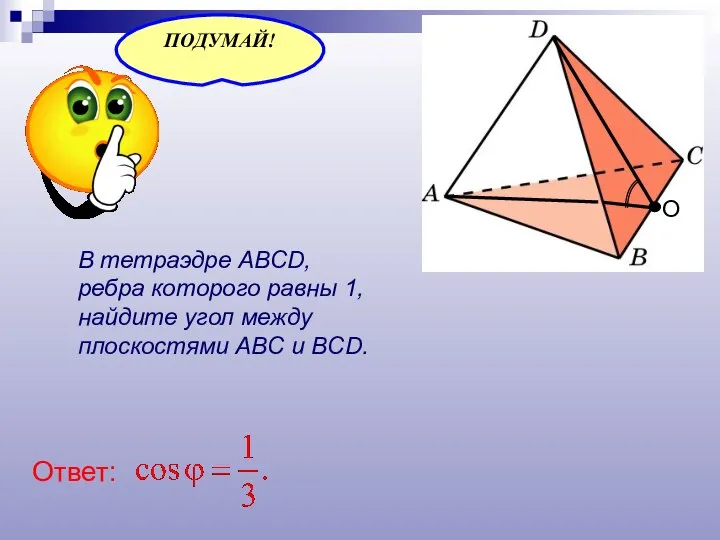
- 25. В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD. О Ответ:
- 27. Скачать презентацию




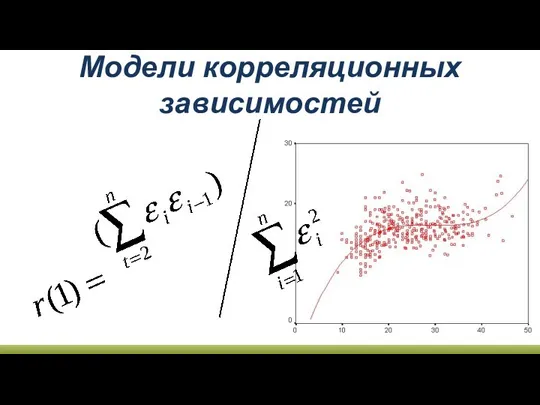 Модели корелляционных зависимостей
Модели корелляционных зависимостей Entrant
Entrant Статистика. Занятие 4
Статистика. Занятие 4 Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Презентация на тему Графики тригонометрических функций
Презентация на тему Графики тригонометрических функций  Сложение до 20. Тренажер по математике. 2 класс
Сложение до 20. Тренажер по математике. 2 класс Задачи на готовых чертежах для подготовки к ЕГЭ
Задачи на готовых чертежах для подготовки к ЕГЭ Трикутники. Елементи трикутника
Трикутники. Елементи трикутника Аналитическое (письменное) счисление координат
Аналитическое (письменное) счисление координат Презентация на тему Деятельностный подход в обучении на уроках математики
Презентация на тему Деятельностный подход в обучении на уроках математики  Подготовка к ПА. Математика
Подготовка к ПА. Математика Задача про чашки
Задача про чашки Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  lecture5
lecture5 Разгадайте загадки
Разгадайте загадки Сложение и вычитание смешанных чисел. 5 класс, урок 96
Сложение и вычитание смешанных чисел. 5 класс, урок 96 Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов Итерактивная мозаика
Итерактивная мозаика Подобие треугольников. Признаки
Подобие треугольников. Признаки Суммирование рядов Фурье методом средних арифметических. Теорема Фейера
Суммирование рядов Фурье методом средних арифметических. Теорема Фейера Математические ребусы
Математические ребусы Презентация на тему Викторина "Ох уж эта математика" 5 класс
Презентация на тему Викторина "Ох уж эта математика" 5 класс  Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Маршрутный лист группы
Маршрутный лист группы Математический диктант по теме Сложение и вычитание. Числа от 11 до 20
Математический диктант по теме Сложение и вычитание. Числа от 11 до 20 Задача о нахождении стороны квадрата
Задача о нахождении стороны квадрата Дискретная математика
Дискретная математика Координаты середины отрезка. Задачи
Координаты середины отрезка. Задачи