Содержание
- 2. Вспоминаем понятия комбинаторики и вероятности. Эти понятия знакомы вам из школьного курса математики. Вспомним методы и
- 3. КОМБИНАТОРИКА – область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или
- 4. КОМБИНАТОРНАЯ ЗАДАЧА – задача, требующая осуществления перебора всех возможных вариантов или подсчета их числа. Понятия
- 5. Задача 1 У кассы кинотеатра стоят четверо ребят. У двух из них сторублевые купюры, у других
- 6. Задача 1 Вариант 1: Вариант 2:
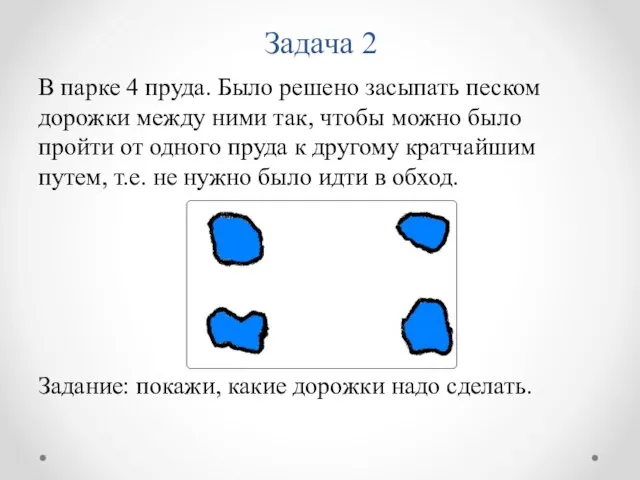
- 7. Задача 2 В парке 4 пруда. Было решено засыпать песком дорожки между ними так, чтобы можно
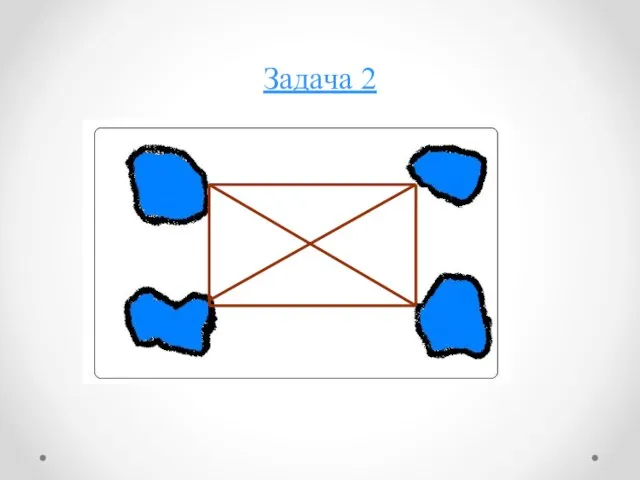
- 8. Задача 2
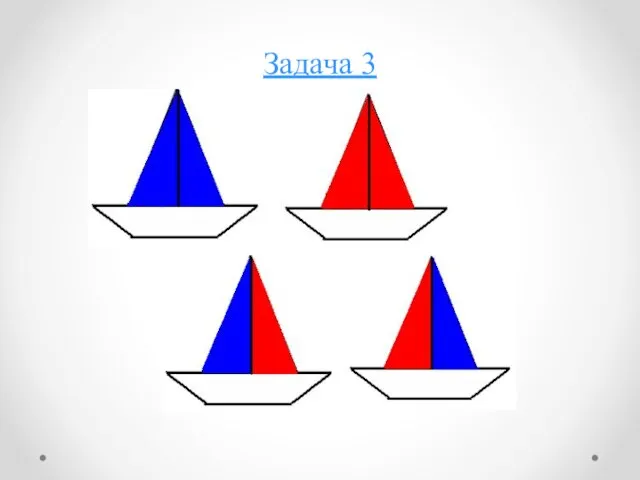
- 9. Задача 3 4 парусника готовились к соревнованиям. У каждого был свой корабль. Судьи решили, что надо
- 10. Задача 3
- 11. Задача 4 На каждом флажке должны быть полоски разного цвета: синяя, красная, черная. Раскрась флажки так,
- 12. Задача 4 6 флажков, т.е. 3 полоски умножаем на 2. в каждой паре меняем местами два
- 13. У Миши 6 яблок. Из них 4 красных и 2 зеленых. Миша съел 3 яблока. Какого
- 14. Задача 5
- 15. Задача 6 Перечислите все двузначные числа, в записи которых встречаются цифры 0, 1, 2.
- 16. Задача 6
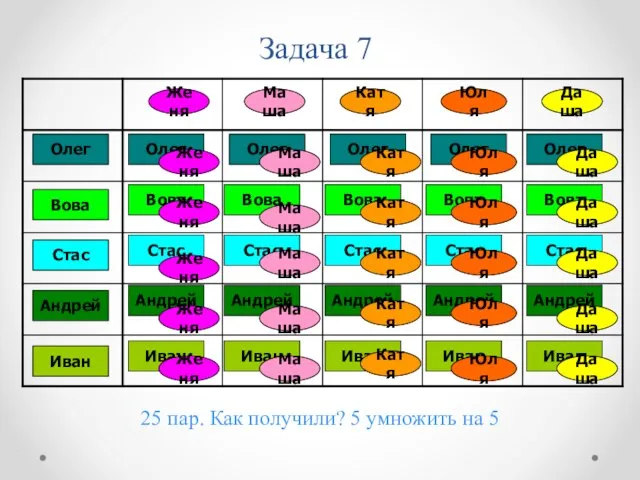
- 17. Задача 7 В танцевальном кружке занимаются пять девочек: Женя, Маша, Катя, Юля и Даша и пять
- 18. Задача 7 25 пар. Как получили? 5 умножить на 5 Женя Маша Катя Юля Даша Олег
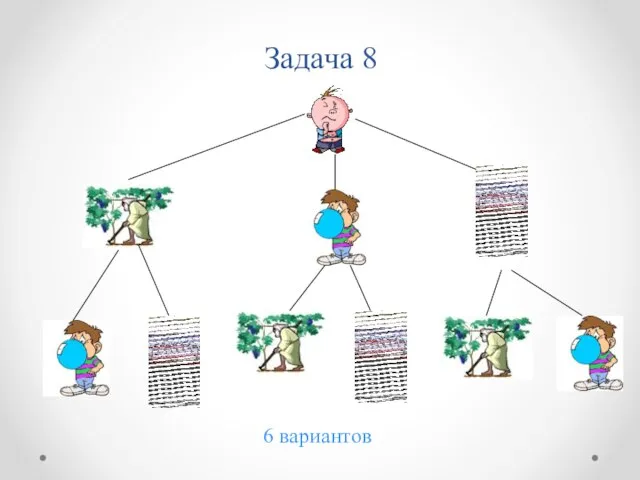
- 19. Задача 8 Миша решил в воскресенье навестить дедушку, своего друга Петю и старшего брата Володю. В
- 20. Задача 8 6 вариантов
- 21. Задача 9 Составь таблицу, соответствующую условию задачи. Сколько завтраков у тебя получилось?
- 22. Задача 9 Задание 1 6 завтраков
- 23. Это были простые задачи, переходим к различным комбинациям
- 24. Перестановки Перестановками из n элементов называют соединения, которые состоят из одних и тех же n элементов
- 25. Посмотрите видео «Комбинаторика. Перестановки» по ссылке: https://www.youtube.com/watch?v=ABMJtIZRsxk
- 26. Задача10 В соревнованиях участвовало 4 команды. Сколько вариантов распределения мест между ними возможно?
- 27. Р4 = 4! = 1· 2· 3· 4 = 24 Ответ: 24.
- 28. Задача 11 Сколькими способами можно разместить 12 человек за столом, возле которого поставлены 12 стульев?
- 29. Р12 = 12! = 479001600 Ответ: 479001600.
- 30. Размещения Размещениями из n элементов называется такие соединения, каждое из которых содержит k элементов, взятых из
- 31. Посмотрите видео урока № 62 «Комбинаторика. Размещение» по ссылке: https://www.youtube.com/watch?v=xCBW1pbRCc8
- 32. Задача 12 Сколько двузначных чисел можно составить из пяти цифр 1,2,3,4,5 при условии, что ни одна
- 33. Решение: Т.к. двузначные числа отличаются друг от друга или самими цифрами, или их порядком, то искомое
- 34. Задача 13 У нас есть 9 книг из серии «Занимательная математика». Сколькими способами можно подарить 3
- 35. Решение: 3 А9 = 9! = 504 (9-3)! Ответ: 504.
- 36. Задача 14 Сколько вариантов расписания можно составить на один день, если всего имеется 8 учебных предметов,
- 37. А³8 = 8 ·7· 6 = 336 Ответ: 336.
- 38. Сочетания Сочетаниями из n элементов по k в каждом называются соединения, каждое из которых содержит k
- 39. Посмотрите видео урок № 63 « Комбинаторика. Сочетания» по ссылке: https://www.youtube.com/watch?v=ZSe1YQXCsj4
- 40. Задача 15 В тренировках участвовали 12 баскетболистов. Сколько различных стартовых пятерок может образовать тренер?
- 41. 5 С12 = 12! = 7!·8·9·10·11·12 = 792 (12-5)!·5! 7!·1·2·3·4·5 Ответ: 792.
- 42. Задача 16 Сколькими способами читатель может выбрать 2 книжки из 6 имеющихся?
- 43. 2 С6 = 6! = 5·6 = 15 4!2! 2 Ответ:15.
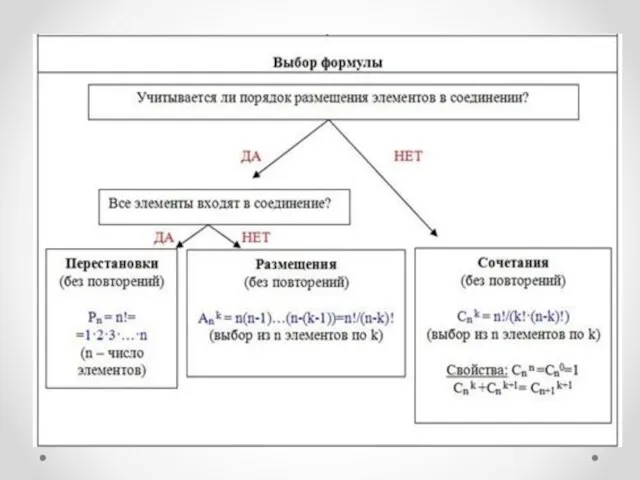
- 44. Теперь все обобщаем. В комбинаторике есть два правила и три формулы.
- 47. Что увидели? При перестановки участвует только одно число И его переставляют А вот определения размещений и
- 48. Вероятность Вероятностью события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих
- 49. Методы решения
- 50. Задача1 Папа, мама, сын и дочка бросили жребий – кому мыть посуду. Найдите вероятность того, что
- 51. Задача 2 Бросают игральную кость. Найти вероятность того, что: а) выпадет четное число очков (А); б)
- 52. Решение. а) На гранях игральной кости имеется три четные цифры (2,4,6), т.е. число искомых исходов m
- 53. Задача 3 Изготовили 100 деталей, из которых 97 стандартных и 3 бракованных. Какова вероятность выбора стандартной
- 54. Решение. Если взять 1 деталь, то событие А – деталь стандартная и событие В – деталь
- 55. И так прочитайте еще раз определения перестановки, размещения и сочетания
- 56. Правило сложения элементарное, задач на него не будет. Произведение применяется тогда, когда есть два разных объекта
- 57. Задача 1 Сколькими способами можно рассадить четверых детей на четырех стульях в столовой детского сада? 4
- 58. Задача 2 Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре
- 59. Задача 3 В группе, в которой 25 студентов, нужно выбрать старосту, его заместителя и помощника заместителя.
- 60. Задача 4 В группе из 25 студентов нужно выбрать не старосту, его заместителя и помощника его
- 61. По вероятности вы разобрали два метода решения задач 1 метод – применение классической формулы 2 метод
- 63. Скачать презентацию






















































 Доверительные интервалы
Доверительные интервалы Длиннее, короче, одинаковые по длине. Математическая сказка
Длиннее, короче, одинаковые по длине. Математическая сказка Обратные тригонометрические функции, их графики и формулы
Обратные тригонометрические функции, их графики и формулы Планиметрия: вычисление площади треугольника
Планиметрия: вычисление площади треугольника Задачи с экономическим содержанием
Задачи с экономическим содержанием Элементы математической статистики. Теория вероятностей
Элементы математической статистики. Теория вероятностей Таблица умножения и деления. Тренажёр на скорость
Таблица умножения и деления. Тренажёр на скорость Шар и сфера
Шар и сфера Письменный прием вычитания
Письменный прием вычитания Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2  Функция, ее график и свойства
Функция, ее график и свойства Таблица. Алгебра
Таблица. Алгебра Основные понятия дискретной математики
Основные понятия дискретной математики Вариационный ряд. Группировка данных при качественной и количественной вариациях
Вариационный ряд. Группировка данных при качественной и количественной вариациях Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Задачи на построение
Задачи на построение Магический квадрат. 2 класс
Магический квадрат. 2 класс Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4
Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4 Природа России в цифрах и загадках
Природа России в цифрах и загадках Действия над матрицами. Вычисление определителей второго и третьего порядков
Действия над матрицами. Вычисление определителей второго и третьего порядков Соответствия между множествами. Отображения. Функции
Соответствия между множествами. Отображения. Функции Математическая модель колонны многокомпонентной ректификации. Лекция 9
Математическая модель колонны многокомпонентной ректификации. Лекция 9 Научные открытия России. Задача тысячелетия. Теорема Пуанкаре
Научные открытия России. Задача тысячелетия. Теорема Пуанкаре Презентация на тему Свойства логарифмов (10 класс)
Презентация на тему Свойства логарифмов (10 класс)  Графики уравнений
Графики уравнений Презентация на тему СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
Презентация на тему СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ  Личные местоимения
Личные местоимения Таблица умножение на двух значное число
Таблица умножение на двух значное число