Следствия из теорем синусов и косинусов

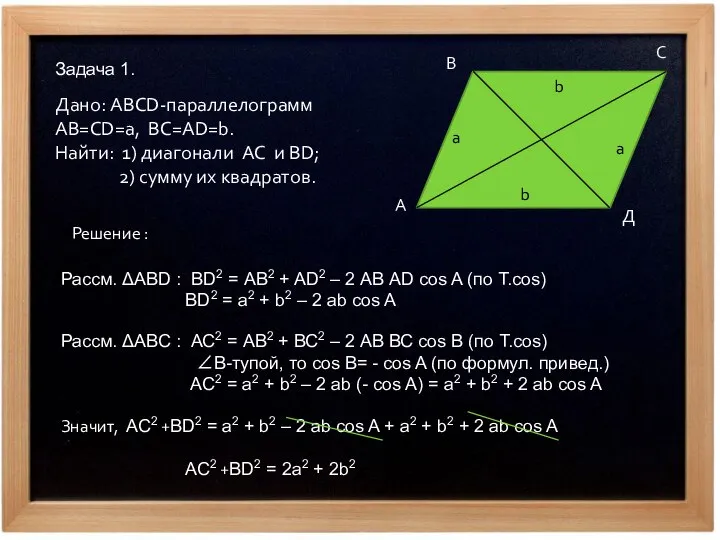
Задача 1.
Дано: ABCD-параллелограмм
AB=CD=a, BC=AD=b.
Найти: 1) диагонали AC и BD;
2) сумму их квадратов.
а
а
b
b
Решение :
Рассм. ΔАВD : BD2 = АВ2 + AD2 – 2 АВ AD cos A (по T.cos)
BD2 = a2 + b2 – 2 ab cos A
А
В
С
Д
Рассм. ΔАВС : АС2 = АВ2 + ВС2 – 2 АВ ВС cos B (по T.cos)
∠B-тупой, то cos B= - cos A (по формул. привед.)
АС2 = a2 + b2 – 2 ab (- cos A) = a2 + b2 + 2 ab cos A
Значит, АС2 +BD2 = a2 + b2 – 2 ab cos A + a2 + b2 + 2 ab cos A
АС2 +BD2 = 2a2 + 2b2

Сумма квадратов диагоналей
параллелограмма равна сумме квадратов всех его сторон.
СЛЕДСТВИЕ 1
d12 +d22 = 2a2 + 2b2

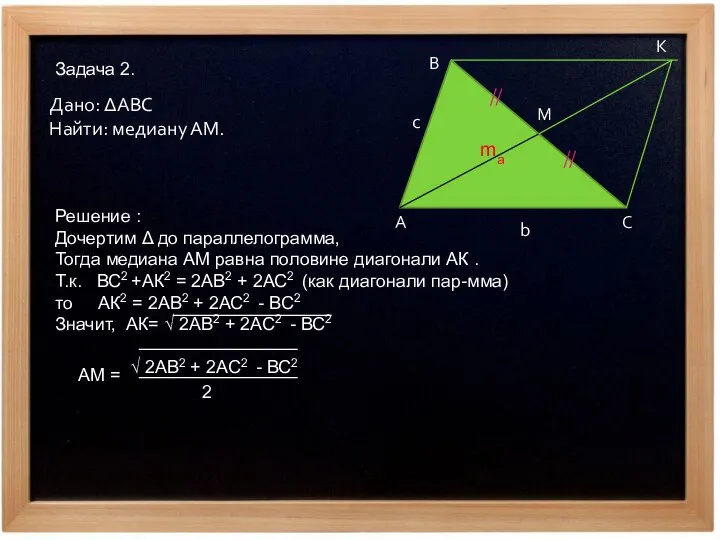
Задача 2.
Дано: ΔABC
Найти: медиану АМ.
А
В
С
M
b
c
ma
Решение :
Дочертим Δ до параллелограмма,
Тогда медиана АМ равна половине диагонали АК .
Т.к. ВС2 +АК2 = 2АВ2 + 2АС2 (как диагонали пар-мма)
то АК2 = 2АВ2 + 2АС2 - ВС2
Значит, АК= √ 2АВ2 + 2АС2 - ВС2
√ 2АВ2 + 2АС2 - ВС2
К
АМ =
2

Длина медианы, проведенной к стороне треугольника равна половине корня квадратного из удвоенной суммы квадратов двух других сторон без квадрата этой стороны.
СЛЕДСТВИЕ 2
m a=
√2(b2 + c2 ) - a2
2

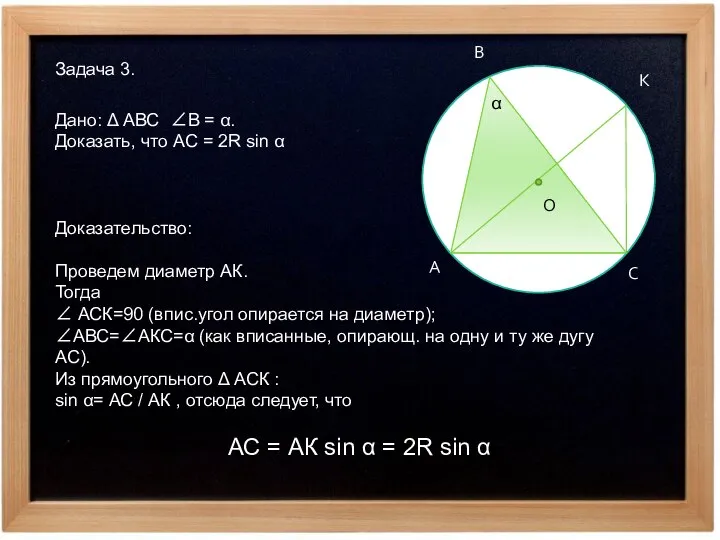
Задача 3.
А
В
С
К
О
Дано: Δ АВС ∠В = α.
Доказать, что АС = 2R sin α
α
Доказательство:
Проведем диаметр АК.
Тогда
∠ АСК=90 (впис.угол опирается на диаметр);
∠АВС=∠АКС=α (как вписанные, опирающ. на одну и ту же дугу АС).
Из прямоугольного Δ АСК :
sin α= АС / АК , отсюда следует, что
АС = АК sin α = 2R sin α