Содержание
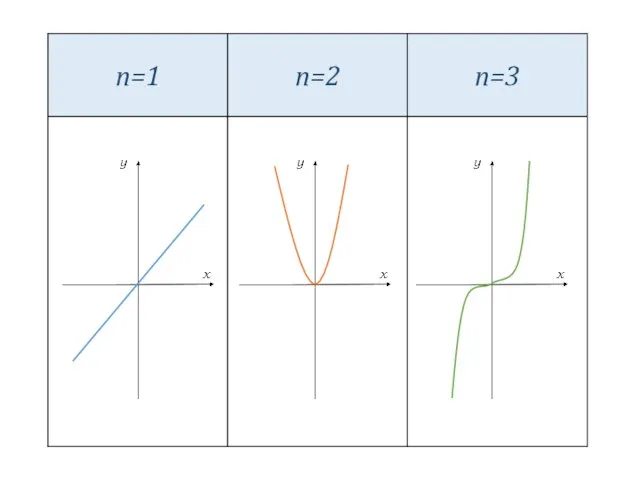
- 2. Заголовок слайда Функция вида у = хr (где r - любое действительное число (в том числе
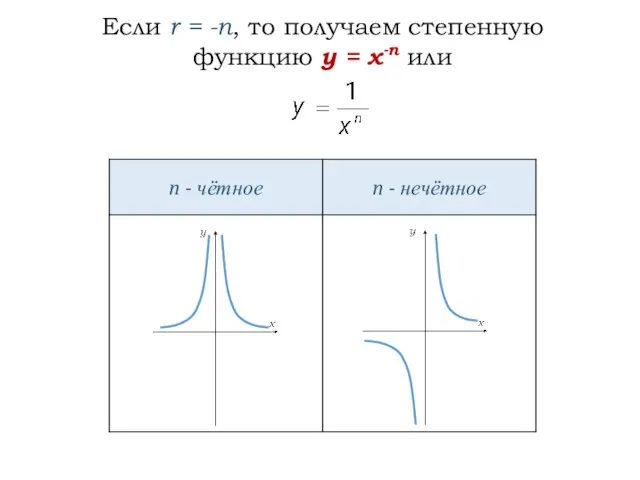
- 4. Если r = -n, то получаем степенную функцию y = x-n или
- 5. При r = 0 имеем функцию y = x0 или у = 1 (где х ≠
- 6. Рассмотрим теперь степенные функции С рациональными показателями степени. Их свойства и графики существенно зависят от показателя
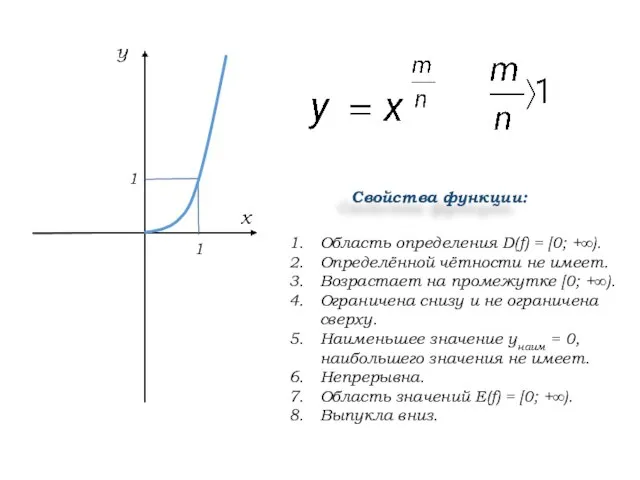
- 7. Область определения D(f) = [0; +∞). Определённой чётности не имеет. Возрастает на промежутке [0; +∞). Ограничена
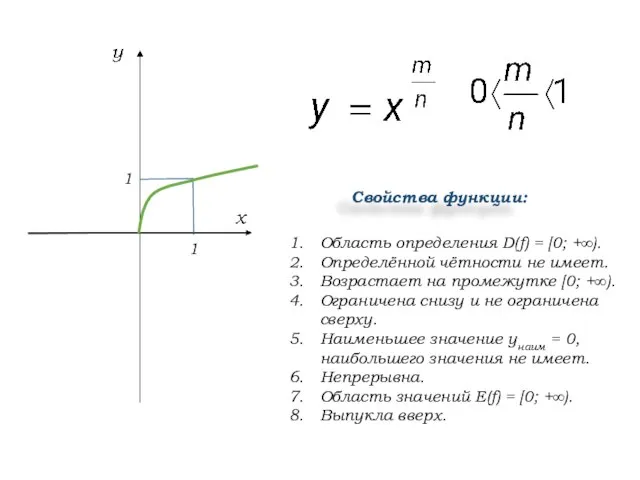
- 8. Область определения D(f) = [0; +∞). Определённой чётности не имеет. Возрастает на промежутке [0; +∞). Ограничена
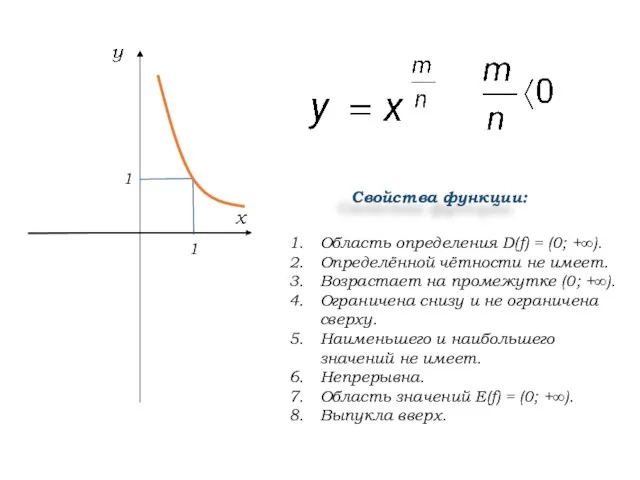
- 9. Область определения D(f) = (0; +∞). Определённой чётности не имеет. Возрастает на промежутке (0; +∞). Ограничена
- 10. Теорема. Если х>0 и r – любое рациональное число, то производная степенной функции y = xr
- 11. Пример 1. Найдём производную функции: При этом было использовано правило дифференцирования
- 12. Пример 2. Исследуем функцию На монотонность и экстремумы и построим её график. 1. Найдём производную функции:
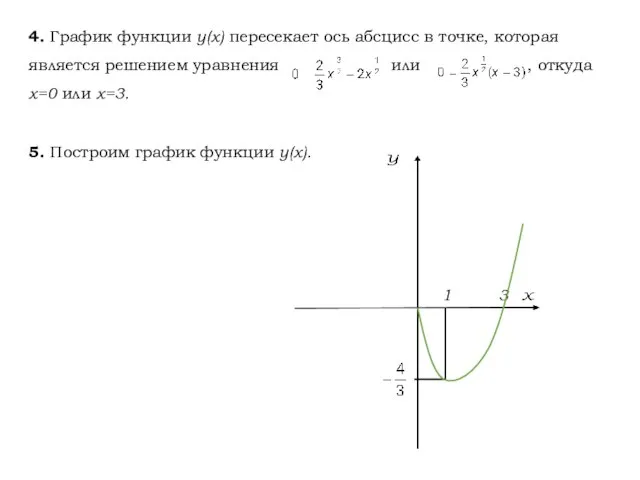
- 13. 4. График функции у(х) пересекает ось абсцисс в точке, которая является решением уравнения или , откуда
- 14. Пример 3. Напишем уравнение касательной к графику функции в точке а = 1. Напомним общий вид
- 15. Контрольные вопросы: 1. Определение степенной функции у = хr. 2. Свойства функции и её график для:
- 17. Скачать презентацию








 Умножение и деление десятичной дроби на единицу с нулями
Умножение и деление десятичной дроби на единицу с нулями Угол между двумя плоскостями
Угол между двумя плоскостями Дискретная математика
Дискретная математика Примеры +7, +8, +9
Примеры +7, +8, +9 Смежные и вертикальные углы
Смежные и вертикальные углы Дифференцирование сложной функции
Дифференцирование сложной функции Первый признак равенства треугольников
Первый признак равенства треугольников Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс
Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс  Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Сложение вида +5. Путешествие в космос
Сложение вида +5. Путешествие в космос Сложение и вычитание целых и дробных чисел
Сложение и вычитание целых и дробных чисел Задачи на проценты
Задачи на проценты Определение производной. Правила вычисления производных. Таблица производных
Определение производной. Правила вычисления производных. Таблица производных 6. СЛАУ. Методы решения (1)
6. СЛАУ. Методы решения (1) Квадратичная функция. Её свойства и график
Квадратичная функция. Её свойства и график Числовые ряды. Признаки сходимости
Числовые ряды. Признаки сходимости Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс
Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс 2.МатСтатистика-Критерии и Различия
2.МатСтатистика-Критерии и Различия Область определения функции
Область определения функции Неопределенный интеграл Ч2, свойства неопределенного интеграла
Неопределенный интеграл Ч2, свойства неопределенного интеграла Графики функций
Графики функций Стереометрия, планиметрия. Основные понятия. (Геометрия. Задания 14, 16)
Стереометрия, планиметрия. Основные понятия. (Геометрия. Задания 14, 16) Равенство треугольников и их элементов. Решение задач
Равенство треугольников и их элементов. Решение задач Презентация на тему Единицы измерения
Презентация на тему Единицы измерения  Проект по математике. Цифра 5. 1 класс
Проект по математике. Цифра 5. 1 класс Презентация на тему Наглядная геометрия для начальной школы
Презентация на тему Наглядная геометрия для начальной школы  Степенная функция
Степенная функция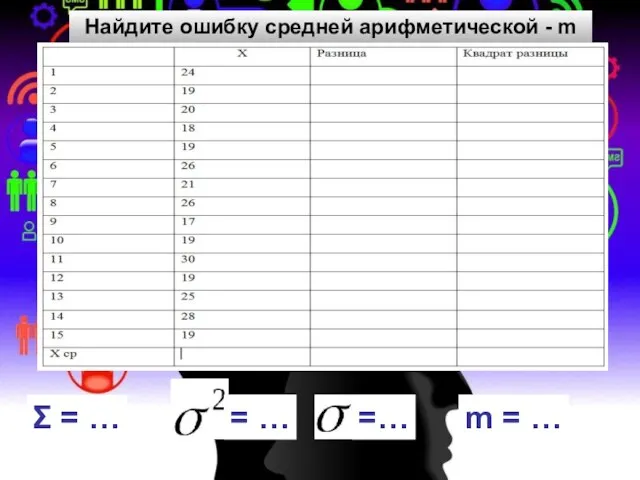 Средняя арифметическая
Средняя арифметическая