Содержание
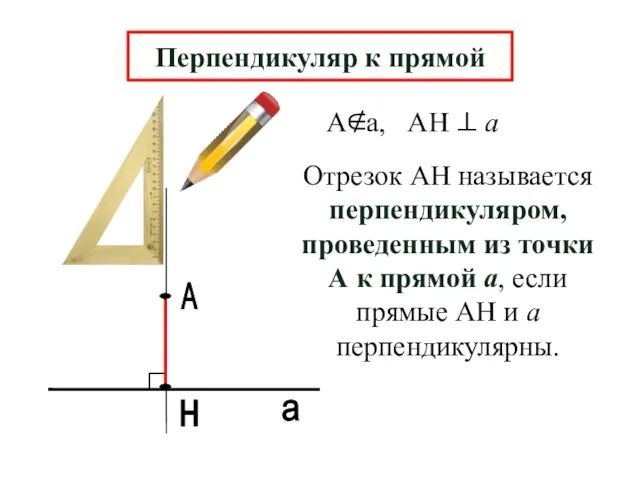
- 2. А н а Перпендикуляр к прямой Отрезок АН называется перпендикуляром, проведенным из точки А к прямой
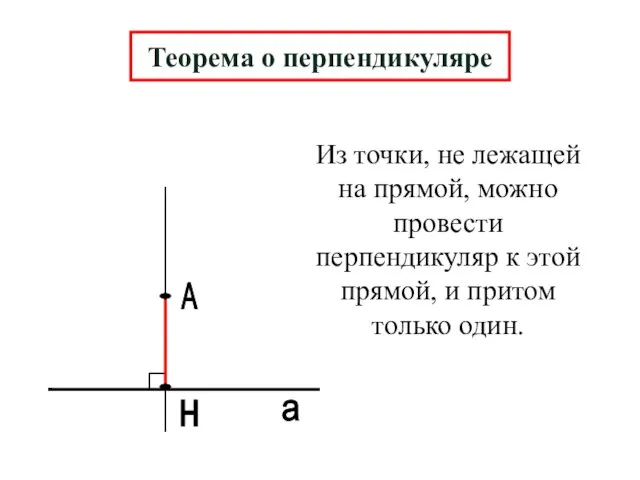
- 3. А н а Теорема о перпендикуляре Из точки, не лежащей на прямой, можно провести перпендикуляр к
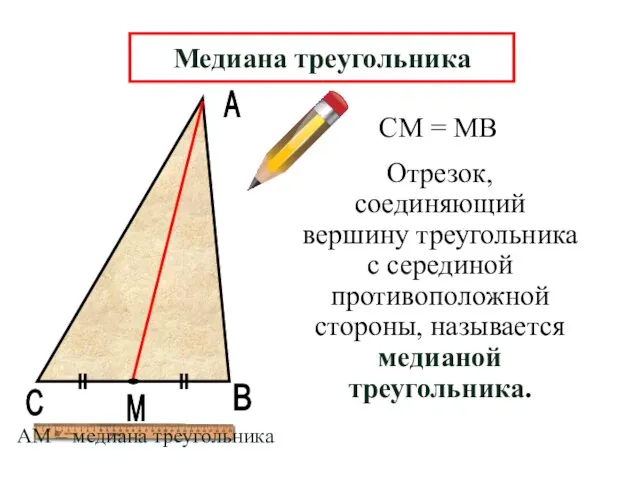
- 4. А В М Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. С СМ
- 5. Медиана-обезьяна, У которой зоркий глаз, Прыгнет точно в середину Стороны против вершины, Где находится сейчас? Медиана
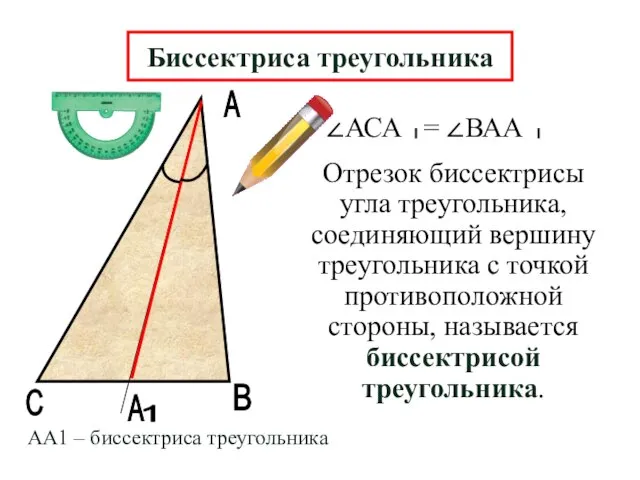
- 6. А В А Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой
- 7. Биссектриса треугольника Биссектриса – это крыса, Которая бегает по углам И делит угол пополам.
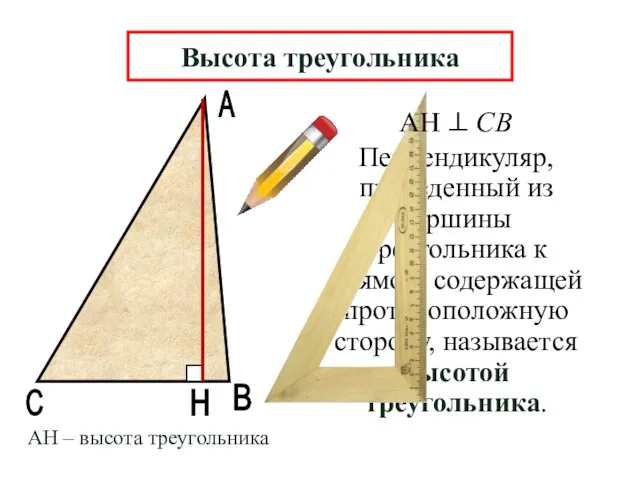
- 8. А В Н Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
- 9. Высота треугольника Высота похожа на кота, Который, выгнув спину, И под прямым углом Соединит вершину И
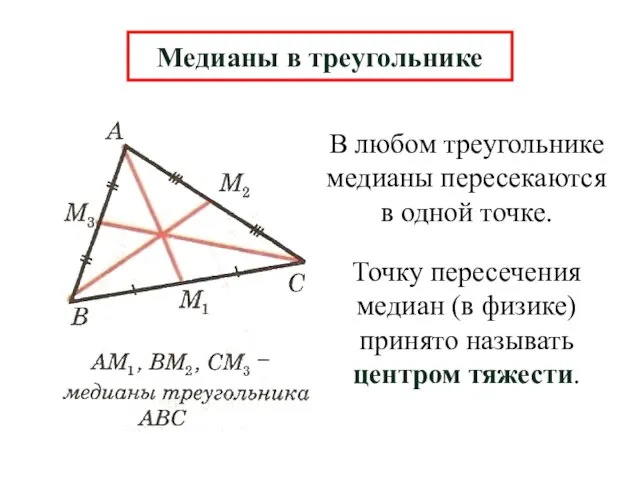
- 10. В любом треугольнике медианы пересекаются в одной точке. Медианы в треугольнике Точку пересечения медиан (в физике)
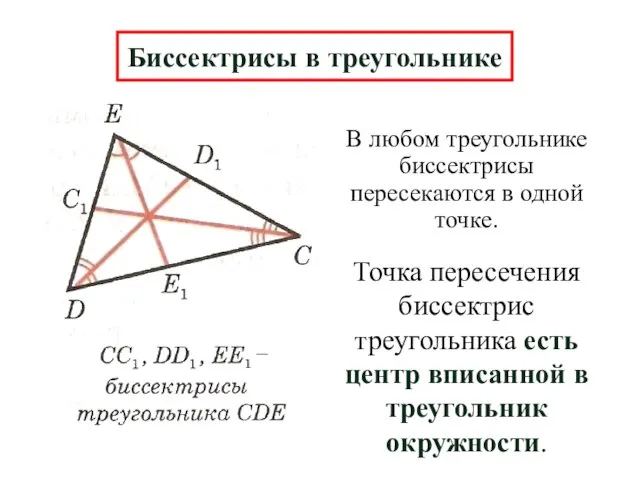
- 11. В любом треугольнике биссектрисы пересекаются в одной точке. Биссектрисы в треугольнике Точка пересечения биссектрис треугольника есть
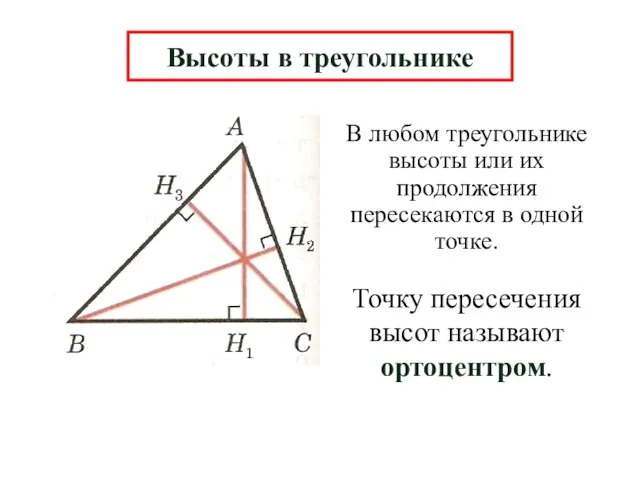
- 12. Высоты в треугольнике
- 13. В любом треугольнике высоты или их продолжения пересекаются в одной точке. Высоты в треугольнике Точку пересечения
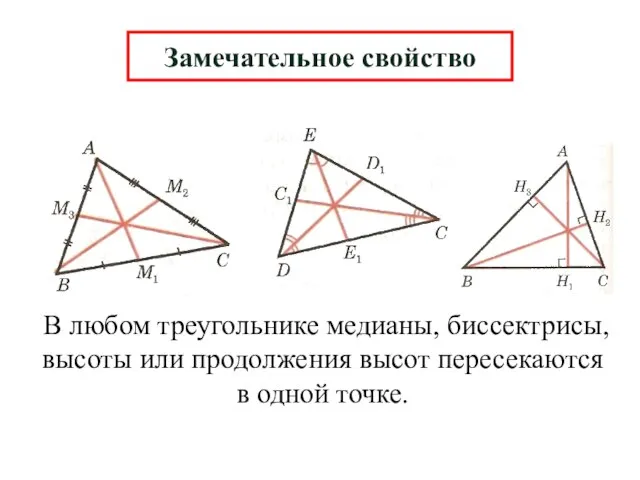
- 14. Замечательное свойство В любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются в одной точке.
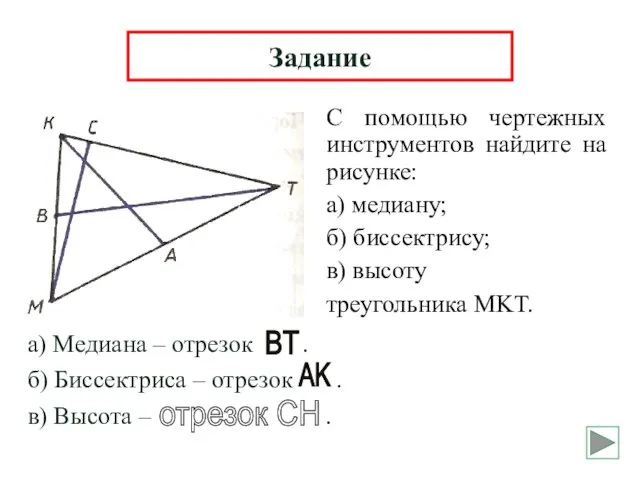
- 15. С помощью чертежных инструментов найдите на рисунке: а) медиану; б) биссектрису; в) высоту треугольника MKT. Задание
- 16. I уровень: п. 16,17, знать основные определения и формулировки утверждений и теорем. II уровень: п. 16,17,
- 18. Скачать презентацию





 Гомотетия. Гомотетичные фигуры
Гомотетия. Гомотетичные фигуры Формула Ньютона-Лейбница. Площадь криволинейной трапеции
Формула Ньютона-Лейбница. Площадь криволинейной трапеции Правила дифференцирования (f(x)+g(x))΄ и (c f(x))΄ Решение задач 11 класс
Правила дифференцирования (f(x)+g(x))΄ и (c f(x))΄ Решение задач 11 класс Презентация на тему Понятие движения
Презентация на тему Понятие движения  Решение задач на межпредметные связи
Решение задач на межпредметные связи Множество. Элемент множества
Множество. Элемент множества Площадь трапеции
Площадь трапеции Тригонометрия. Сумма и разность синуса, косинуса
Тригонометрия. Сумма и разность синуса, косинуса Презентация на тему Деление и дроби (5 класс)
Презентация на тему Деление и дроби (5 класс)  Конструирование из геометрических фигур
Конструирование из геометрических фигур Математическое моделирование. Контурно-графический анализ
Математическое моделирование. Контурно-графический анализ Кенгуру – математика для всех
Кенгуру – математика для всех Теория вероятности в жизни пчел
Теория вероятности в жизни пчел Неравенства и их системы
Неравенства и их системы Теорія ймовірностей, ймовірнісні процеси і математична статистика
Теорія ймовірностей, ймовірнісні процеси і математична статистика Сравнение натуральных чисел
Сравнение натуральных чисел Задачи на проценты
Задачи на проценты Цифры в буквах
Цифры в буквах Математические станции
Математические станции Неравенства системы и совокупности неравенств
Неравенства системы и совокупности неравенств Симметрия. Симметричные объекты. Платоновы тела
Симметрия. Симметричные объекты. Платоновы тела Lecture 6. Techniques of Integration (part 1)
Lecture 6. Techniques of Integration (part 1) Аксиомы стереометрии
Аксиомы стереометрии Тригонометрические функции
Тригонометрические функции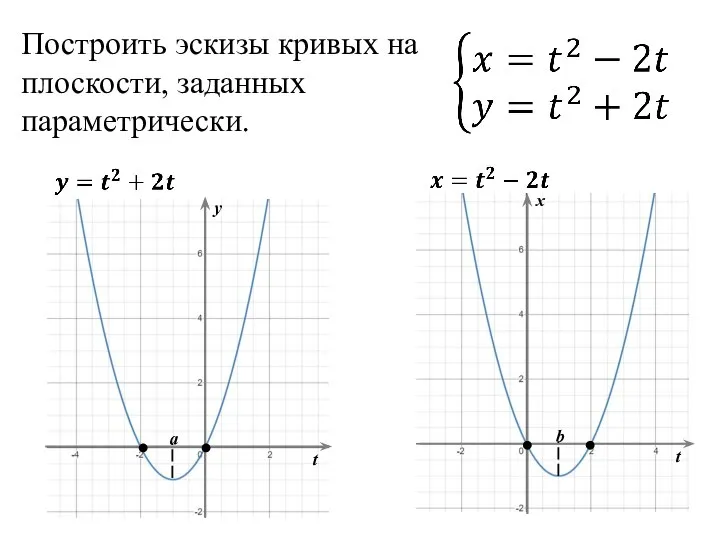 Построить эскизы кривых на плоскости, заданных параметрически
Построить эскизы кривых на плоскости, заданных параметрически Свойства логарифмов
Свойства логарифмов Информационные технологии образовании
Информационные технологии образовании Прямая. Ортогональные проекции прямой линии
Прямая. Ортогональные проекции прямой линии