Полином Жегалкина

Теорема.
Любая функция алгебры логики от n переменных может быть представлена полиномом Жегалкина и это представление единственно.

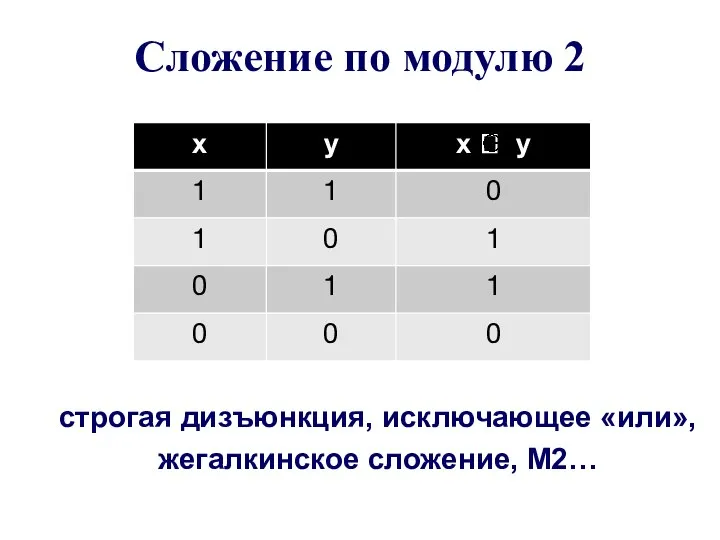
Сложение по модулю 2
строгая дизъюнкция, исключающее «или», жегалкинское сложение, M2…

Свойства операции сложение по модулю 2
Возможно разложение в СДНФ
(освобождение от М2 или строгой дизъюнкции)

Свойства операции сложение по модулю 2
Связь между дизъюнкцией
и суммой по модулю два (строгой дизъюнкцией)
Операции с константами

Полином (многочлен) Жегалкина: функция от 2 логических переменных
полиномиальные коэффициенты (принимают значение равное 0 или 1)
функция от 3 логических переменных

Полином (многочлен) Жегалкина от n логических переменных:
Всего здесь 2ⁿ слагаемых.
ꚛ - означает сложение по модулю 2,
Все полиномиальные коэффициенты являются константами (равными нулю или единице).

Алгоритм построения ПЖ
(с помощью эквивалентных преобразований)
Минимизируем булеву функцию любым известным нам способом
Заменяем дизъюнкцию суммой по модулю 2
3. Заменяем
Используем распределительный закон
(раскрываем скобки)
5. Применяем и

Метод неопределенных коэффициентов
(по таблице истинности или вектору значений функции)

Иван Иванович Жегалкин (1869-1947) – российский и советский математик и логик, профессор Московского университета. Заслуженный деятель науки РСФСР один из основоположников современной математической логики. Из его открытий наибольшую известность получил так называемый полином Жегалкина. Жегалкин награжден Орденом Трудового Красного Знамени.
Жегалкин предложил в 1927 году в качестве
удобного средства для представления функ-
ций булевой логики многочлен, названный
полиномом Жегалкина.
Известный советский математик Николай
Лузин, вспоминая студенческие годы,
говорит, что из профессоров не боялся лишь
Жегалкина.

А теперь самостоятельно потрудимся над получением полинома Жегалкина
в тетрадях.

Вариант А

Вариант Б

Вариант В

Вариант Г

Вариант Д

Дополнительное задание.
Пусть функция задана вектором значений
f = (11001011).
Найти полином Жегалкина.