замене (4.5) левая полуплоскость P-плоскости и левая часть основной полосы Q-плоскости преобразуются в круг единичного радиуса с центром в начале координат (рис. 1, в).
С учётом обозначения (4.5) формулу (4.4) перепишем в виде
(4.6)
Полученное выражение является главной частью ряда Лорана, Лорана, представляющего функцию X(z) в Z-плоскости. Функция комплексного аргумента X(z) есть одностороннее Z-преобразование или просто Z-преобразование решётчатой функции x[n].
Если оригиналы x(t) и x[n] являются вещественными функциями, то комплексным полюсам их изображений X(p) в P-плоскости, X(q) в Q-плоскости и X(z) в Z-плоскости соответствуют комплексно-сопряжённые полюсы в этих плоскостях (на рис.1 полюсы pi и p*i, qi и q*i, zi и z*i). В случае же комплексных оригиналов x(t) и x[n] это свойство не выполняется.


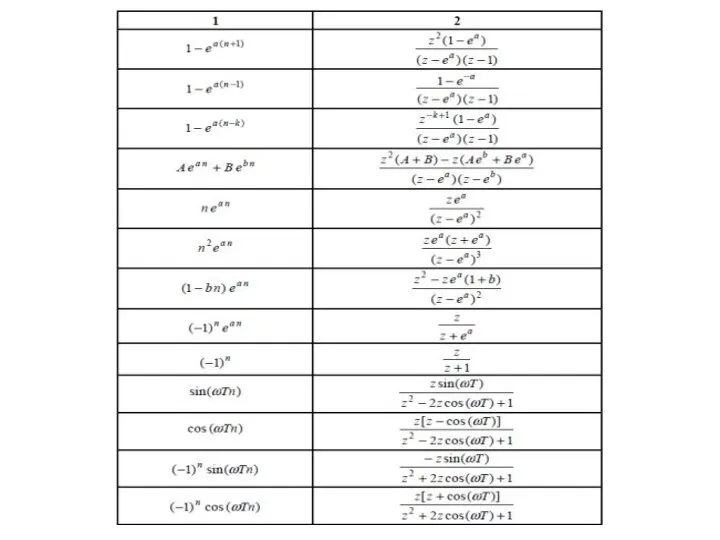




![Эта формула представляет дискретное преобразование Лапласа (ДПЛ) решётчатой функции x[n], в которой](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1150570/slide-8.jpg)
![Рис.1. Расположение комплексно-сопряжённых полюсов изображений вещественных сигналов x(t) и x[n]: a —](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1150570/slide-9.jpg)


 Интенсив ЦОКО по математике
Интенсив ЦОКО по математике Презентация на тему Почему нельзя жить без математики?
Презентация на тему Почему нельзя жить без математики?  Презентация на тему Натуральные логарифмы
Презентация на тему Натуральные логарифмы  Площадь многоугольников. Решение задач
Площадь многоугольников. Решение задач Деление на 3
Деление на 3 Решение логарифмических неравенств
Решение логарифмических неравенств Устный счёт
Устный счёт Задачи на построение угла
Задачи на построение угла Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 16
Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 16 Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Вычисление определенных интегралов
Вычисление определенных интегралов Квадратичная функция у=х2 и ее свойства
Квадратичная функция у=х2 и ее свойства Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Односторонние пределы
Односторонние пределы Математика с котом Леопольдом
Математика с котом Леопольдом Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана
Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана Презентация на тему Числовые промежутки
Презентация на тему Числовые промежутки  Алгоритм исследования функции одного аргумента
Алгоритм исследования функции одного аргумента Задачи на призму
Задачи на призму Метод Гаусса
Метод Гаусса Генеральная средняя
Генеральная средняя Анализ контрольной работы по геометрии
Анализ контрольной работы по геометрии теорема Виета
теорема Виета Криволинейные интегралы
Криволинейные интегралы Случайные события. Вероятности и частоты
Случайные события. Вероятности и частоты Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Презентация на тему Теорема о сумме углов треугольника
Презентация на тему Теорема о сумме углов треугольника  Приёмы вычитания с переходом через десяток
Приёмы вычитания с переходом через десяток