Tema1_TeoriaMnozhestv

ВЫПИСКА ИЗ УЧЕБНОГО ПЛАНА
1 академический час – 45 астрономических минут
Лк – 32 ч (16 занятий)
Практ – 64 ч (32 занятия)
I семестр – экзамен

ДОПУСК К ЭКЗАМЕНУ
1. Посещаемость занятий
2. Успеваемость (лекционные конспекты, выполнение практических заданий в указанный срок)
3. Отработка пропущенных занятий: конспекты, защита реферата (4 ч. пропуска = 1 реферат)
4. Бонусы: участие в конференциях, подготовка статей к публикации

СТУДЕНЧЕСКИЙ КРУЖОК «СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В МАТЕМАТИКЕ»

СТУДЕНЧЕСКИЙ КРУЖОК «СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В МАТЕМАТИКЕ»

HTTPS://URAIT.RU

ЗАРЕГИСТРИРОВАТЬСЯ В СИСТЕМАХ
https://lk.chuvsu.ru

https://moodle.chuvsu.ru

https://moodle.chuvsu.ru

Пароль dm

ВВЕДЕНИЕ
Дискретная математика (дискретный анализ) – совокупность математических дисциплин, изучающих свойства абстрактных дискретных (прерывных) объектов.
Для сравнения, объектом изучения в классической математике выступают непрерывные объекты

НАУЧНЫЕ НАПРАВЛЕНИЯ, СПОСОБСТВУЮЩИЕ РАЗВИТИЮ ДИСКРЕТНОЙ МАТЕМАТИКИ:
Теоретическая кибернетика,
Теория кодирования,
Теория графов,
Математическая логика
Теория автоматов и т.д.

ТЕМА 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

ПЛАН
1. Основные понятия.
2. Операции над множествами.
3. Соответствия между множествами.
4. Классификация множеств. Мощность множества
5. Кортежи. Декартовы произведения
6. Отношения

СПИСОК ЛИТЕРАТУРЫ
Пак, В. Г. Дискретная математика: теория множеств и комбинаторный анализ. Сборник задач : учебное пособие для вузов / В. Г. Пак. — Москва : Издательство Юрайт, 2020. — 235 с. — Текст : электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/453113.
Вороненко А. А. Дискретная математика: задачи и упражнения с решениями : учебно-методическое пособие / Вороненко А. А., Федорова В. С. - Москва: Инфра-М, 2014. – 104 с.

3. Палий, И. А. Дискретная математика и математическая логика : учебное пособие для вузов / И. А. Палий. — 3-е изд., испр. и доп. — Москва : Издательство Юрайт, 2020. — 370 с. — Текст : электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/447489.
4. Тишин В. В. Дискретная математика в примерах и задачах: [учебное пособие] / Тишин В. В. - СПб: БХВ-Петербург, 2017. – 335 с.

1. ОСНОВНЫЕ ПОНЯТИЯ
Множество, элементы множества - первичные базисные неопределяемые понятия теории множеств.
Совокупность элементов, объединенных некоторым признаком, свойством, составляет понятие множество.

Например, множество книг в библиотеке, множество студентов в группе, множество натуральных чисел N, множество букв русского алфавита, множество делителей числа 100 и т.д.
Приведите примеры множеств.

Иллюстрация кругами Эйлера (а ∈ М, b ∉ М)

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА
1) перечисление всех элементов, например,
A={2, 4 , 7, 8, 11}, B={0, 1};
2) указание свойств, которым обладают те и только те элементы, которые принадлежат данному множеству, например, A={x| x-10>20}.

Если множество не содержит элементов, обладающих характеристическим признаком, то оно называется пустым и обозначается ∅. Например, множество целых решений неравенства 5 < х < 6 является пустым:
A={х| х ∈ Z, 5 < х < 6} = ∅.
Множество, не являющееся пустым, называется непустым.

Множество К, все элементы которого обладают таким же признаком, что и элементы множества М, называют подмножеством множества М и обозначают К ⊂ М .
Иллюстрация кругами Эйлера (K⊂M)

Например, множество целых чисел Z является подмножеством множества рациональных чисел Q.
Для числовых множеств справедливо соотношение: N ⊂Z⊂Q⊂R⊂C, где N – множество, натуральных чисел, Q – рациональных, R – действительных, С – комплексных чисел.

Для любого непустого множества М справедливо:
M⊂M,
∅⊂M

Универсальным называют множество U, состоящее из всех возможных элементов, обладающих данным признаком.

Например, множество планет Солнечной системы:
U = {Земля, Марс, Венера, Юпитер, Сатурн, Уран, Меркурий, Нептун}.
Понятие универсального множества четко не определено, т.е. некорректно.

Равными называют два множества А и В, состоящие из одинаковых элементов. Обозначение: А = В.
А={x | 4х-8 = 0}, B={x | logх4=2}, A=B
Равны множества букв, из которых составлены слова «навес» и «весна».

Количество элементов множества А называется мощностью множества (кардинальным числом) и обозначается |А| или n(А).

Например
А – множество букв русского алфавита.
|А| = 33

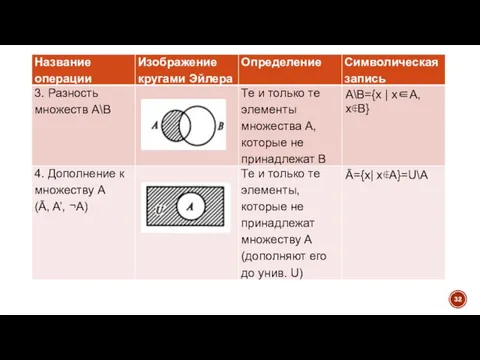
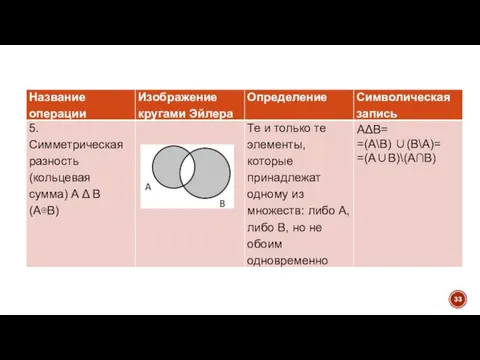
2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

СВОЙСТВА ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ
l. A∪B=B∪A; А∩В=В∩А — переместительный закон (коммутативность) для операций объединения и пересечения.
2. (A∪B)∪C = A∪(B∪C); (А∩В)∩ С = А∩(В∩ С) - сочетательный закон (ассоциативность) для операций объединения и пересечения.

СВОЙСТВА ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ
3. (A ∪ В)∩ С = (А ∩ С) ∪ (В ∩ С) — распределительный закон (дистрибутивность) пересечения относительно объединения множеств.
4. (А∩В)∪ С = (A∪ С)∩(В∪ С) — распределительный закон объединения относительно пересечения множеств.

5. A∪A = A, A∩A = А, А ⊂ (A∪B) — законы поглощения.
6. U=∅' и ∅ = U', т.е. универсальное и пустое множества являются дополнениями друг друга.

7. Если обозначить через Аi все подмножества А1, А2, А3, ..., Аn множества А, то будут справедливы равенства:

8. Для любого множества Х⊂ U справедливо (X') ' = X.
9. Для любых двух множеств X и Y справедливо: если X ⊂U, У⊂ U, то (X∩Y)' = X'UY' или (X∪Y)' = X' ∩ Y'.

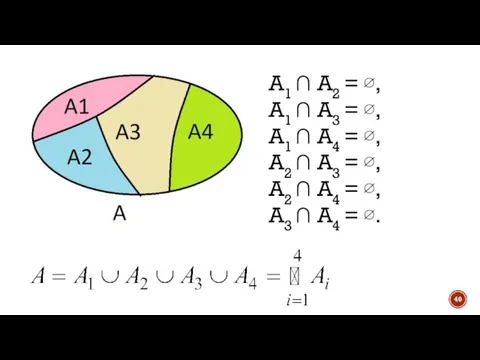
10. Множество А можно разбить на классы непересекающихся подмножеств Ai, если:
• объединение всех подмножеств совпадает с множеством А:
• пересечение любых двух различных подмножеств пусто, т.е. ∀ i ≠ j выполняется
Аi ∩ Aj= ∅.

A1 ∩ A2 = ∅,
A1 ∩ A3 = ∅,
A1 ∩ A4 = ∅,
A2 ∩ A3 = ∅,
A2 ∩ A4 = ∅,
A3 ∩ A4 = ∅.

3. СООТВЕТСТВИЯ МЕЖДУ МНОЖЕСТВАМИ
Пусть даны два множества А= {а1, a2, ...} и В={b1, b2 ...}.
Тогда пары (ai, bj) задают соответствие между множествами А и В, если указано правило R, по которому для элемента ai из множества А выбирается элемент bj из множества В.

Например, русско-английский словарь устанавливает соответствие значений и написаний слов русского и английского языков.

Пусть задано соответствие R между множествами А и В, т. е. R: (a; b),
a ∈ A, b ∈ В.
Для некоторого элемента а множества А поставлен в соответствие некоторый элемент b из множества B, который называется образом элемента а:
b = R(a).
Тогда а = R-l(b) – прообраз элемента b ∈ В,
Каждому прообразу соответствует единственный образ.

Образ множества А при соответствии R называется множеством значений этого соответствия и обозначается R(A), если R(A) состоит из образов всех элементов множества А:
R(A) = {b| ∀ a ∈A, b = R(a)}.

Прообраз множества В при некотором соответствии R называют областью определения этого соответствия и обозначают R-l(B), т.е.
R-l(B) = {a| ∀b ∈ В, ∃a∈ A: R(a) = b},
здесь R-l является обратным соответствием для R.

Для описания соответствий между множествами используют понятие отображения (функции) одного множества на другое.
Для задания отображения необходимо указать:
• область определения данного отображения D(f);
• множество значений этого отображения E(f);
• закон, или, соответствие f между этими множествами.
Обозначение f: A → В

Пусть G – график соответствия R: X→Y, т.е. множество пар вида (x,y), x∈X, y∈Y:
G={(x,y)| x∈X, y∈Y}.
Область определения соответствия R обозначим пр1G,
область значений соответствия R обозначим пр2G.
Соответствие R называется всюду определенным, если пр1G=X.
Соответствие R называется сюръективным, если пр2G=Y.

Соответствие R называется функциональным (функцией), если его график не содержит пар с одинаковыми первыми и различными вторыми координатами.
Соответствие R называется инъективным, если его график не содержит пар с одинаковыми вторыми и различными первыми координатами.

Соответствие называется взаимно-однозначным, если оно функционально и инъективно.
Соответствие называется биекцией, если оно всюду определено, сюръективно, функционально и инъективно.

Пример
Даны множества X={a, b, c, d},
Y = {1, 2, 3, 4, 5}, A = {a, b), B = {3, 4} и
график соответствия G = {(a, 2),(b, 1), (b, 5), (d, 4)}.
Определить, является ли соответствие всюду определённым, сюръективным, функциональным, инъективным.
Найти образ R(А) и прообраз R-1(В).

Решение:
Построим соответствующий граф
G = {(a, 2),(b, 1), (b, 5), (d, 4)}

Соответствие не всюду определено, так как np1G={a, b, d}≠X.
Соответствие не сюръективно, так как np2G = {1, 2, 4, 5} ≠ Y.
Соответствие не функционально, так как его график содержит две пары (b, 1)и
(b, 5) с одинаковыми первыми и различными вторыми координатами (из точки b выходят две стрелки).
Соответствие инъективно, так как его график G не содержит пар с одинаковыми вторыми и различными первыми координатами (ни в одну точку множества Y не входят две или более стрелки).

2. Найдём образ R(А) и прообраз R-1(В).
R(А) = {1, 2, 5}, так как
A = {a, b} и {(a, 2), (b, 1), (b, 5)} ⊂ G .
R-1(B) = {d}, так как В = {3, 4} и только (d, 4) ∈ G .

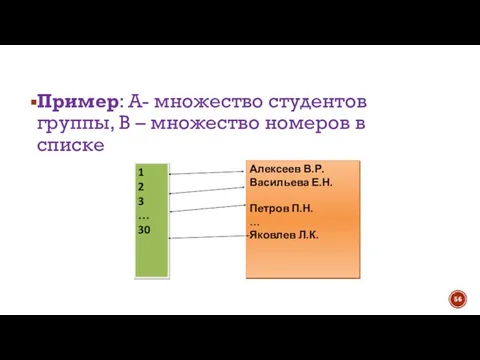
Если между элементами множеств А и В установлено взаимно-однозначное соответствие, то эти множества имеют одинаковое количество элементов.
В таком случае говорят, что множеств А и В равносильны, равномощны, или эквивалентны.

Пример: А- множество студентов группы, В – множество номеров в списке

Отображение е: А → А называется тождественным (единичным), если каждому аргументу оно ставит в соответствие себя. Отображение, обратное единичному, также является единичным.
Примеры тождественных отображений:

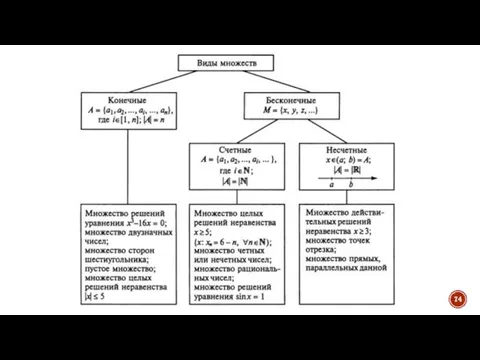
4. КЛАССИФИКАЦИЯ МНОЖЕСТВ. МОЩНОСТЬ МНОЖЕСТВА
Количество элементов, содержащихся во множестве А, называется мощностью множества А (или кардинальным числом) и обозначается |A|.
Если мощность множества может быть выражена вполне определенным числом, то множество называется конечным, в противном случае - бесконечным

Если множества конечны, то сравнивают их мощности.
Обозначим через А, В, С, D соответственно множества букв слов «крот», «корт», «кран» и «рот». Тогда |А| =|В| = |С| = 4, |D| = 3.
Следовательно, А, В и С имеют равные мощности, а мощность D меньше, чем, например, мощность A: |D| < |А|, так как 3 < 4.
Множества А, В и С равномощны.
Обозначение: A~B, A ~C
Понятие «равномощные множества» не означает, что они обязательно равны.

Булеаном множества М называется множество всех его подмножеств, которое обозначается 2М,
т.е. 2М = {А | А ⊂ М}.
Для конечного множества М мощность булеана равна |2M| = 2|M|.

В частности, множество всех подмножеств любого конечного множества, состоящего из n элементов, является конечным множеством, состоящим из 2n элементов.

Пример:
Дано множество А = {a, b, c},
Его мощность n = |A| = 3
Булеан множества А:
2A={{∅}, {a}, {b}, {c}, {a,b}, {a,c}, {b,c} {a,b,c}}
Мощность булеана равна | 2A |=2|A|=23=8.

ОСНОВНАЯ ТЕОРЕМА О КОНЕЧНЫХ МНОЖЕСТВАХ
Любое конечное множество не эквивалентно никакому его собственному подмножеству, кроме самого себя.
Следствие. Всякое непустое конечное множество эквивалентно одному и только одному отрезку натурального ряда чисел (1, ..., n).

Эталоном для сравнения бесконечных множеств служит натуральный ряд чисел N.
Бесконечное множество, эквивалентное множеству натуральных чисел N, называется счетным. Говорят, что все элементы счетного множества можно пронумеровать. В противном случае бесконечное множество будет несчетным.

Г. Кантор в 1878 году доказал, что несчетно множество точек, расположенных на отрезке [0; 1].
По определению Б. Больцано (1837) и Р. Дедекинда (1887) множество называется бесконечным, если оно равномощно одному из своих собственных подмножеств.

ИНТЕРЕСНЫЕ ВОПРОСЫ
Равна ли часть целому? Часть меньше целого?
Каких чисел больше: натуральных N или рациональных Q? рациональных Q или действительных R?
Где больше точек: на отрезке или на всей прямой?
на прямой или в квадрате?
Где больше точек, на отрезке длиной в 1 мм или на отрезке длиной в 1 м?

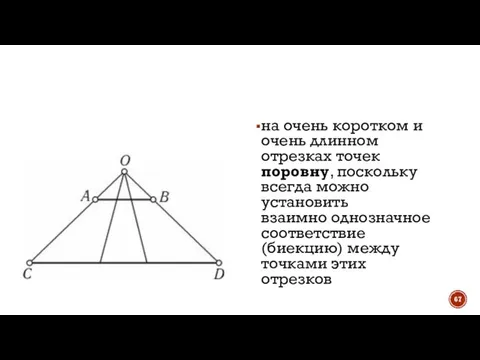
на очень коротком и очень длинном отрезках точек поровну, поскольку всегда можно установить
взаимно однозначное соответствие (биекцию) между точками этих отрезков

Поскольку для бесконечных множеств нельзя указать число, которое является его мощностью, принято их сравнивать по эквивалентным им основным множествам N и R.

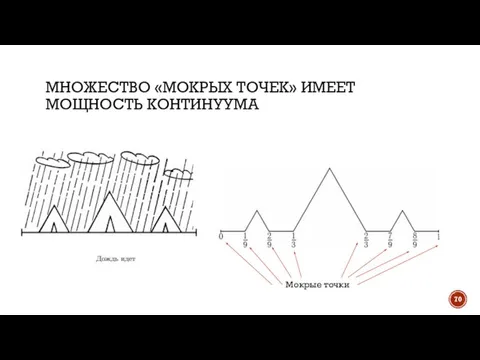
Всякое бесконечное множество, равносильное множеству действительных чисел, называется множеством мощности континуума (от лат. continuum — непрерывный). Условное обозначение: |R|.
Так, множество А точек прямой несчетно и имеет мощность континуума: |A| = |R|.

МНОЖЕСТВО «МОКРЫХ ТОЧЕК» ИМЕЕТ МОЩНОСТЬ КОНТИНУУМА
Мокрые точки

ТЕОРЕМЫ О БЕСКОНЕЧНЫХ МНОЖЕСТВАХ
1. Мощность бесконечного множества не изменяется от прибавления к нему счетного множества.
2. Мощность несчетного множества не меняется от удаления из него счетного множества.

АРИФМЕТИКА БЕСКОНЕЧНОГО: ОПЕРАЦИИ НАД МОЩНОСТЯМИ
Обозначим: - мощность счетного множества (читается: алеф нуль),
- мощность континуума, f - мощность множества всех функций, заданных на действительной оси

1) сумма конечного и счетного множеств является счетным множеством
2) сумма двух счетных множеств есть счетное множество
3) прибавление
счетного множества к множеству мощности континуума дает множество мощности континуума
4) и 5) описать самостоятельно

ТЕОРЕМЫ О МОЩНОСТИ МНОЖЕСТВ
1. Если А ⊂ B то |А| <|В|.
2. Если А ~ C ⊂ B, В ~ D ⊂ А, то |А| = |В|.
3. Если К ⊂ М и К несчетно (|K|=|R|), то М тоже несчетно (|M|=|R|).

5. КОРТЕЖИ. ДЕКАРТОВЫ ПРОИЗВЕДЕНИЯ
Пусть А — конечное множество (|A|=n),
F: А → {1, 2, ..., n} –правило, по которому нумеруются элементы множества А
Кортежем длины n называется последовательность
, упорядоченная по правилу F.
Для задания кортежа важен порядок.

Кортежи <а1, а2, ..., аk> и
называются равными, если они имеют одинаковую длину и их элементы с одинаковыми номерами совпадают.

Например, равны кортежи
<21, 22, 23, 24, 25> и <2, 4, 8, 16, 32>, так как оба кортежа имеют длину 5 и равны все соответствующие пары:
21 = 2; 22 = 4; 23 = 8; 24 = 16; 25 = 32.

Из двух данных кортежей <а1, а2, ..., аk> длины k и b2, ..., bm> длины m можно составить два новых кортежа
<а1, а2, ..., аk, b1, b2, ..., bm>
и
длины k+m.
Эта операция называется соединением кортежей.

Например, даны кортежи <2, 5, 9>
и
Варианты соединения кортежей:
<2, 5, 9, a, b> и

Пусть заданы множества А1, А2, ..., Аn.
Декартовым (прямым) произведением этих множеств называется множество
А1 × А2 × ... × Аn, состоящее из всех кортежей
<а1, а2, ..., аn> длины k, в которых ак∈Ак, где 1 ≤k ≤ n.
Поскольку для задания кортежа важен порядок, то порядок множителей важен и в декартовом произведении.
Свое название декартово произведение получило в честь выдающегося французского математика и философа Рене Декарта (1596-1650).

Пример: декартовым произведением множеств А = {0,1} и
В = {X, Y, Z} является множество пар
А×В = <(0; X), (0; Y), (0; Z), (1; X), (1; Y), (1; Z)>.
Или в виде таблицы

Если А1 = А2 =... = Аn = А, то пишут
и называют n-й декартовой степенью множества А.

Например, плоскость (в геометрии) является декартовым квадратом двух прямых и обозначается R2 , пространство (в геометрии) является декартовым квадратом трех прямых и обозначается R3

В физике пространственно-временной континуум есть декартово произведение R3 х Т,
где R3 — трехмерное пространство, а T— числовая ось времени.

Проекцией вектора (a1, a2,…,an) на ось i называется координата ai.
Графиком Р называется подмножество декартова произведения двух множеств.

Инверсией графика называется график
P-1={(a, b)|(b, a)∈P}.
Композицией графиков P и Q называется график
P°Q={(a, b) | ∃x ((a, x) ∈P и (x, b) ∈Q)}.

Пример
Даны графики P={(1;1), (1;2), (2;3), (2;2)} и Q={(1;5), (1;6), (3;6)}.
Найти: а) P-1; б) P°Q; в) пр1P; г) пр2Q.

Решение:
P={(1;1), (1;2), (2;3), (2;2)},
А) P-1={(1;1), (2;1), (3;2), (2;2)} – инверсия графика P

P={(1;1), (1;2), (2;3), (2;2)},
Q={(1;5), (1;6), (3;6)}.
Б) P°Q={(1;5), (1;6), (2;6)} – композиция графиков P и Q

P={(1;1), (1;2), (2;3), (2;2)},
Q={(1;5), (1;6), (3;6)}.
В) пр1P={1; 2} – первая проекция графика P,
Г) пр2Q={5; 6} – вторая проекция графика Q.
Ответ: а) {(1;1), (2;1), (3;2), (2;2)}; б) {(1;5), (1;6), (2;6)}; в) {1; 2}; г) {5; 6}.

СВОЙСТВА ДЕКАРТОВА ПРОИЗВЕДЕНИЯ КОНЕЧНЫХ МНОЖЕСТВ
|А × В| = |А| ⋅ |В|
А × В ≠ В × А
Если А1 = А2 =... = Аn = А, то |Аn| = |А|n

АРИФМЕТИКА БЕСКОНЕЧНОГО: СВОЙСТВА ДЕКАРТОВА ПРОИЗВЕДЕНИЯ
1) × =
2) × =
3) × =
1) декартово произведение счетных множеств счетно (или сумма счетного множества счетных множеств является счетным множеством)
2) декартово произведение счетного множества и множества мощности континуума есть множество мощности континуума
3) число точек на отрезке и в квадрате совпадает

6. ОТНОШЕНИЯ
Соответствие между равными множествами А = В называется отношением на данном множестве (А).
Отношения в некоторых числовых множествах могут выражаться терминами: «быть равным», «быть больше», «быть не меньше», «быть делителем» и т.д.

Отношения во множестве линий на плоскости могут выражаться терминами: «быть параллельными», «пересекаться», «касаться» и т.д.
Отношения являются частным случаем отображения, когда область определения и множество значений совпадают

Назовем n-местным отношением ϕ на непустом множестве A подмножество R ⊂ An.
При n=2 отношение ϕ называется бинарным.
Или:
Бинарным отношением на множестве А называется пара
Ф = (A, G), где А - область задания отношения, G - график отношения, причём G ⊂ А .

Если (х, у) ∈ G, то вводят обозначение xϕу и говорят, что х и у вступают в отношение ϕ (находятся в отношении ϕ).
Если х и у не вступают в отношение ϕ, обозначают
Диагональю множества А2 называется график
ΔA = {(х, х) | х ∈ А)

Например,
а||b (параллельные прямые),
а ≤ b (действительные числа),
а = logc b
y=sin x
x≠y
y=tgx и т.д.

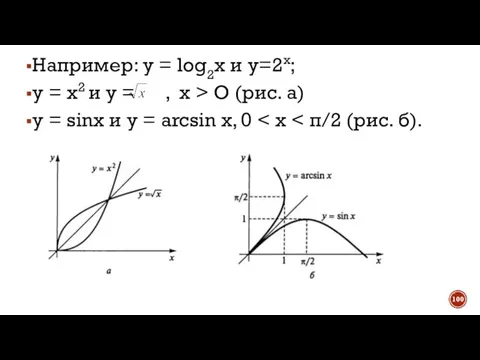
Графики прямых и обратных бинарных отношений, определенных на множестве действительных чисел, симметричны относительно биссектрисы I и III квадрантов.
Это свойство обратных бинарных отношений используют при построении графиков обратных функций. Построение однозначной обратной функции возможно лишь для монотонных функций.

Например: у = log2x и у=2х;
у = х2 и у = , х > О (рис. а)
у = sinx и у = arcsin x, 0 < х < π/2 (рис. б).

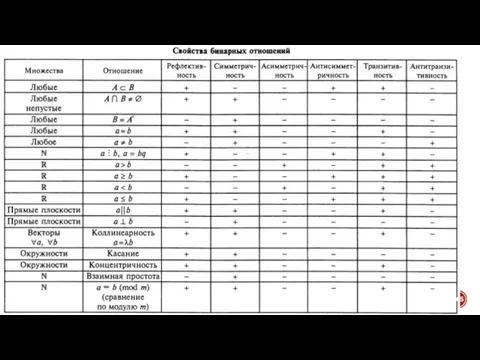
СВОЙСТВА БИНАРНЫХ ОТНОШЕНИЙ:
Рефлексивность (рефлективность): ∀ х∈A (хϕх)
С помощью графиков отношений можно записать: ΔА ⊆ G
Например, «быть не больше» на R.
2. Антирефлексивность: ∀ х∈A .
ΔА ∩ G = ∅
Имеет место, когда отношение ϕ не обладает свойством рефлективности для любых х, например «быть больше», «быть младше» и др.

3. Симметричность: ∀ х∈A, ∀ y∈A (хϕy → yϕx)
G = G -1
Или, одновременно выполняются хϕy и yϕx
Например, симметрична параллельность прямых, так как если а || b, то b || а. Симметрично отношение «быть равным» на любом множестве или «быть взаимно-простым» на N.
4. Антисимметричность. Если для несовпадающих элементов x≠y, верно отношение хϕy, то ложно yϕx (∀x, y ∈ A)
Например: отношения «быть больше», «не меньше» на R, «быть делителем» на N и др.
G ∩ G-1 ⊆ ΔА

5. Транзитивность. Если хϕy и yϕz, то xϕz, ∀x, y, z ∈ A.
G ° G ⊆ G
Например: отношения «быть больше», «быть параллельным», «быть равным» и др.
6. Антитранзитивность. Имеет место, когда отношение не обладает свойством транзитивности.
Например, «быть перпендикулярным» на множестве прямых плоскости ( а ⊥ b, b ⊥ с, но неверно a ⊥ с).

7. Асимметричность. Ни для одной пары x и y (∀x, y ∈ A) не выполняется одновременно хϕy и yϕx.
8. Связность. Для любых ∀x, y ∈ A, x≠y выполняется хϕy или yϕx.
A2 \ ΔA ⊆ G ∪ G-1
Заметим, что каждое конкретное отношение может обладать или не обладать некоторыми из указанных свойств.

Если даны два отношения: Φ = (A, G) и Ψ = (A, F ), то операции над этими отношениями сводятся к операциям над их графиками:
Φ ∪ Ψ = (A ,G ∪ F ), объединение
Φ ∩ Ψ = (A ,G ∩ F ), пересечение
Φ \ Ψ = (A ,G \ F ), разность
Φ Δ Ψ = (A ,G Δ F ), симметрическая разность
=(A, A2 \ G), дополнение

ВИДЫ БИНАРНЫХ ОТНОШЕНИЙ
Отношение ϕ называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно

∀x, y, z ∈ A
• xϕx (рефлекcивность);
• если x ϕ y, то у ϕ х (симметричность);
• если x ϕ y, y ϕ z, то x ϕ z (транзитивность).
Обозначение: a Q b или а ~ b,
Например, «быть равным на множестве чисел», быть подобным на множестве геометрических фигур.

Непересекающиеся подмножества, на которые разбивается множество А отношением эквивалентности ϕ, называются классами эквивалентности.

Множество всех различных классов эквивалентности называется фактор-множеством множества А по отношению эквивалентности ϕ (обозначается А / ϕ).
Мощность фактор-множества А / ϕ называется индексом разбиения,
порождённого отношением ϕ.

Например, множество всех рациональных чисел Q можно разбить на классы эквивалентности, для которых а/b — рациональная дробь,
где a ∈ Z; b ∈ N.
Любая дробь с/b будет отнесена к тому же классу тогда и только тогда, когда ad = bc, т.е. а/b и c/d эквивалентны, если ad = bc
(например, -2/4 ~ -3/6).

ПРОВЕРИМ ВЫПОЛНИМОСТЬ СВОЙСТВ ДЛЯ ТАКОГО ОТНОШЕНИЯ:
рефлексивность
Для любой дроби а/b выполняется равенство
ab = bа, значит
а/b Q а/b, или а/b ~ а/b
симметричность
если а/b ~ c/d, то ad = be, но be = ad, значит c/d ~ а/b

транзитивность
Пусть что а/b ~ c/d, c/d ~ m/n.
Докажем, что а/b ~ m/n, т.е. an = bm.
Действительно, так как а/b ~ c/d, то ad = bc (*),
аналогично, c/d ~ m/n, то сn = md (**).
Умножим равенство (*) на n, а (**) на b,
тогда имеем adn = bcn и bcn = mdb.
По свойству транзитивности adn = mdb или an = mb. Чтд.
Такие дроби классифицируются по элементу, порождающему класс эквивалентности, которым в этом примере является несократимая дробь (например, для 2/4 ~ 3/6 ~ 4/8 таковой будет 1/2).

2. Отношение ϕ на множестве А называется отношением толерантности, если оно рефлексивно и симметрично.

Предыдущее отношение эквивалентности есть частный случай толерантности, когда к двум перечисленным свойствам добавляется транзитивность.

Например, отношение «быть другом» рефлексивно, симметрично, но не транзитивно.
Толерантность является более слабой мерой сходства, чем эквивалентность, но тем не менее помогает выявлять различия в схожих вещах. Дает интуитивное представление о сходстве объектов.

3. Отношение ϕ называется отношением порядка на множестве А, если оно антисимметрично и транзитивно.
Обозначение: (x предшествует y).
Множество A, которое обладает отношением порядка, называется упорядоченным.

Отношение называется отношением частичного порядка, если оно рефлексивно, антисимметрично и транзитивно.
Отношение называется отношением линейного порядка, если оно является отношением частичного порядка и связно.

Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.
Отношение называется отношением строгого линейного порядка, если оно - связное отношение строгого порядка.

Рефлективное отношение порядка называют отношением нестрогого порядка и обозначают знаком ≤.
Антирефлективное отношение порядка называют отношением строгого порядка и обозначают знаком <.

На множестве A задано отношение полного порядка, если сравнимы все элементы этого множества. Такое множество называется вполне упорядоченным.
На множестве A задано отношение частичного порядка, если сравнимы не все элементы этого множества. Такое множество называется частично упорядоченным.

Отношение порядка дает возможность сравнивать между собой различные элементы множества А.
Пусть А — упорядоченное множество с отношением строгого порядка <. Об упорядоченной паре х < у говорят, что элемент х предшествует элементу у.

Пусть А — вполне упорядоченное множество. Тогда, если для элемента х не нашлось предшествующего, то он называется минимальным.
Т.е. не существует элементов у, «меньших», чем х.
Символическая запись:

На множестве N натуральных чисел выполняются лишь свойства антисимметричности и транзитивности.
Поэтому на нем установлено отношение полного порядка: для любой пары натуральных чисел единица является предшествующим числом, т.е. минимальным.

Можно доказать, что конечное вполне упорядоченное множество содержит единственный минимальный элемент.
Например, на множествах чисел Z, Q, R отношения ≤ и ≥ есть отношения нестрогого полного порядка, а отношения < и > есть отношения строгого полного порядка.
Отношение ⊂ есть отношение нестрогого частичного порядка на множестве 2A (булеан).