Свойства функции

Алгоритм исследования функции
1. Область определения
2. Множество значений
3. Чётность , нечётность
4. Периодичность
5. Непрерывность
6. Промежутки возрастания и убывания
7. Ограниченность функции
8. Нули функции
9. Точки экстремума (наибольшее и наименьшее значение функции)
10. Выпуклость графика
Выпуклость

1. Область определения
Область определения функции у = f(x) - это множество всех действительных значений переменной х , при которых функция имеет смысл. Обозначение: Д(х).
Область определения функции у =
Д(х)= (- , т. к. подкоренное выражение всегда больше или равно нулю.

2. Множество значений
Множество значений функции у = f(x) - это множество всех действительных значений переменной у , которые функция может принимать при данном х. Обозначение: Е(у).
Множество значений функции у =
Е(у)= , т. к. значение подкоренного выражения всегда больше или равно нулю.

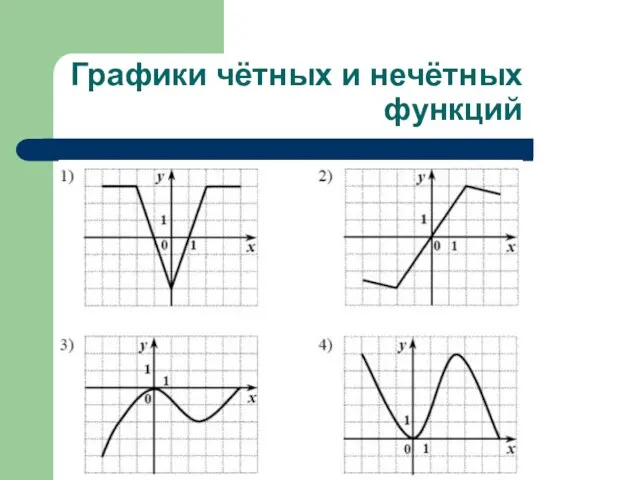
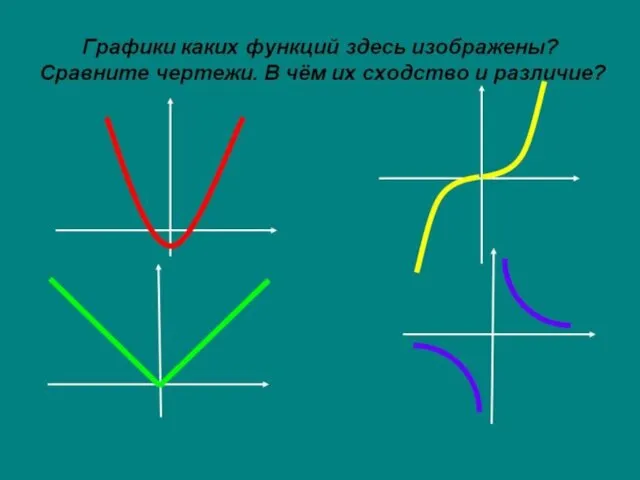
3.Чётность и нечётность функции
Функцию у = f(x) называют чётной, если для любого значения х из множества Д(х) выполняется равенство
Функцию у = f(x) называют нечётной, если для любого значения х из множества Д(х) выполняется равенство
Функция у = f(x) не является ни чётной, ни нечётной, если хотя бы в одной точке из множества Д(х) выполняются неравенства

Особенности графиков функций
Если график функции симметричен относительно оси ординат Оу, то функция чётная.
Если график функции симметричен относительно начала координат, то функция нечётная.
Если график функции не симметричен, то функция не является ни чётной, ни нечётной.

Графики чётных и нечётных функций

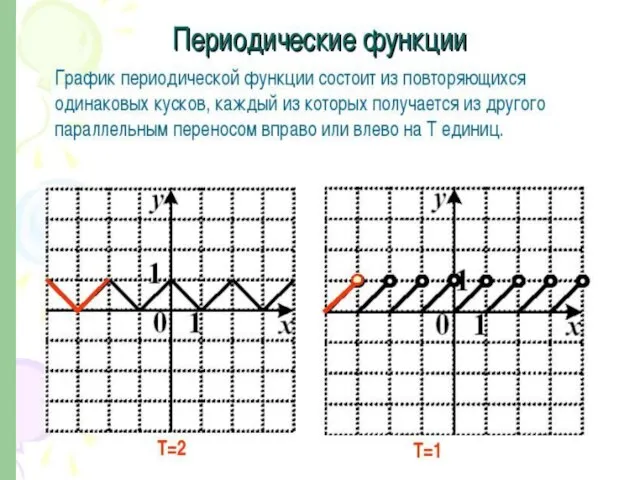
4. Периодичность функции
Периодическая функция ― функция, повторяющая свои значения через некоторый регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу х некоторого фиксированного ненулевого числа (периода функции) на всей области определения.
Функция называется периодической, если существует такое число T≠0 (период), что на всей области определения функции Д(х) выполняется равенство .

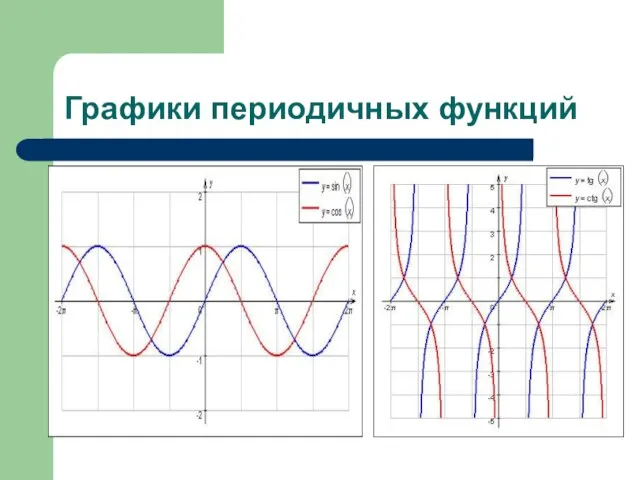
Графики периодичных функций

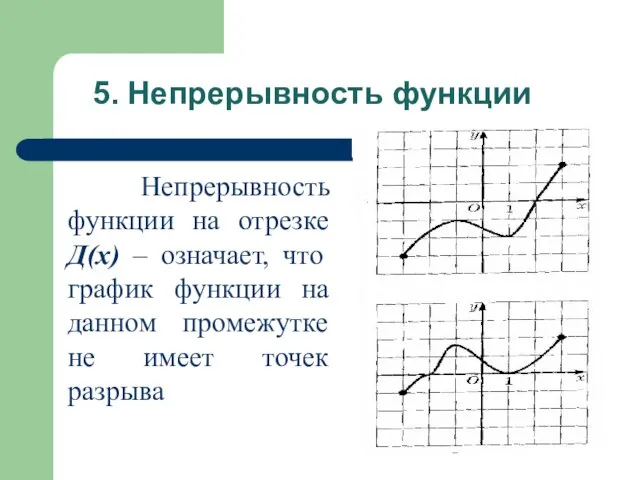
5. Непрерывность функции
Непрерывность функции на отрезке Д(х) – означает, что график функции на данном промежутке не имеет точек разрыва

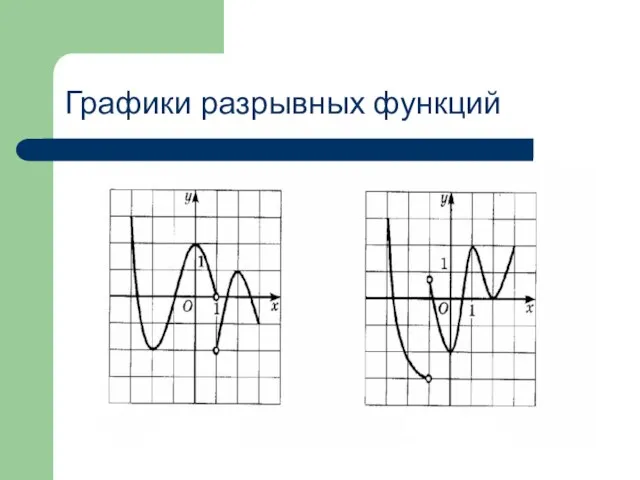
Графики разрывных функций

Термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
6. Монотонность функции

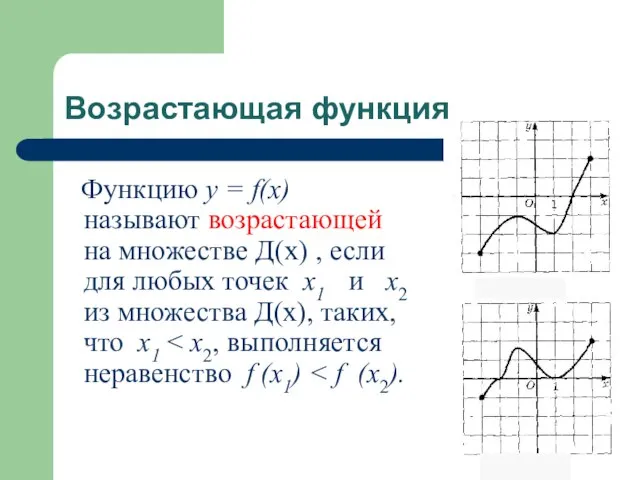
Возрастающая функция
Функцию у = f(x) называют возрастающей на множестве Д(х) , если для любых точек x1 и x2 из множества Д(х), таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).

Условие возрастания
Функция возрастает, если большему значению аргумента соответствует большее значение функции.

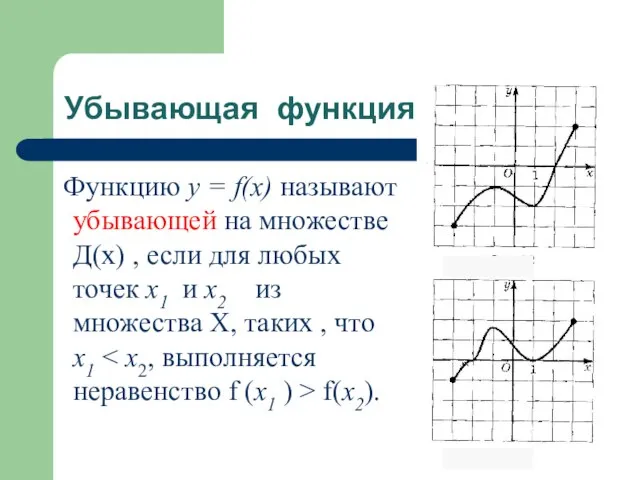
Убывающая функция
Функцию у = f(x) называют убывающей на множестве Д(х) , если для любых точек x1 и x2 из множества Х, таких , что x1 < x2, выполняется неравенство f (x1 ) > f(x2).

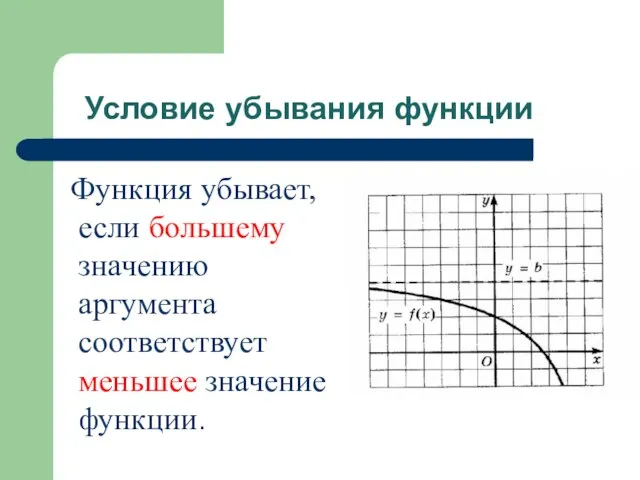
Условие убывания функции
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

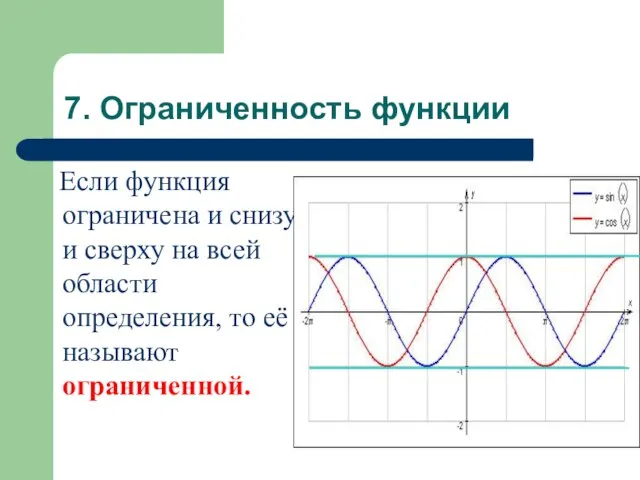
7. Ограниченность функции
Если функция ограничена и снизу и сверху на всей области определения, то её называют ограниченной.

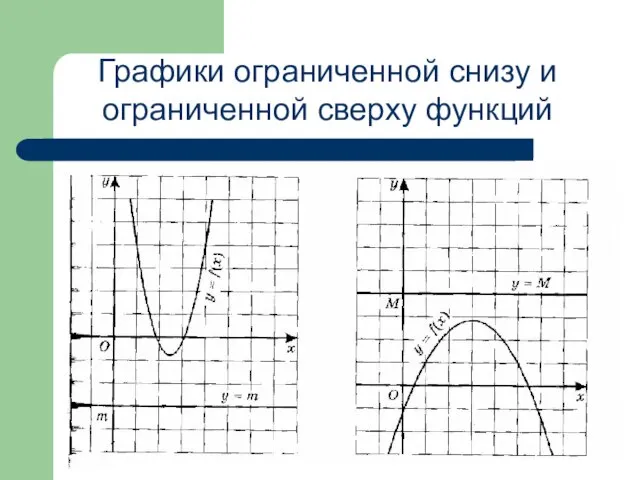
Ограниченность снизу
Функцию у= f(x) называют ограниченной снизу на множестве Д(х), если все значения этой функции больше некоторого числа m, т.е. существует такое число m, что для любого значения х выполняется неравенство f(x) > m

Ограниченность сверху
Функцию у=f(x) называют ограниченной сверху на множестве Д(х) , если все значения этой функции на множестве Д(х) меньше некоторого числа М , т.е. существует такое число М , что для всех значений х выполняется неравенство f(x) < М

Графики ограниченной снизу и ограниченной сверху функций

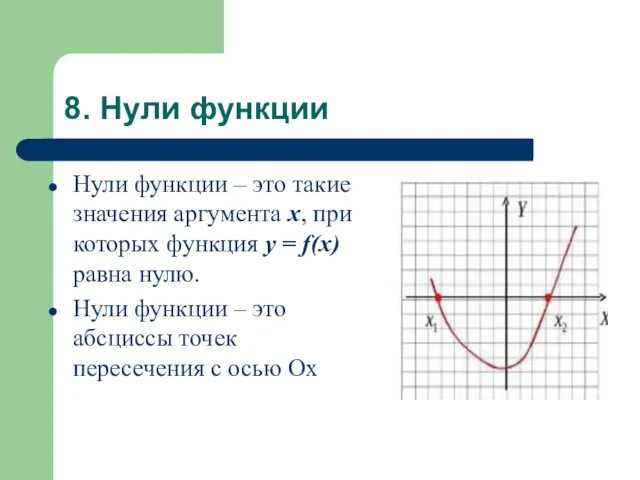
8. Нули функции
Нули функции – это такие значения аргумента х, при которых функция у = f(x) равна нулю.
Нули функции – это абсциссы точек пересечения с осью Ох

9. Наименьшее значение
функции
Число m называют наименьшим значением функции у = f(x) на множестве Д(х) , если:
1)во множестве Х существует такая точка x0 , что f(x0) = m
2) для любого значения х из множества Х выполняется неравенство

Наибольшее значение функции
Число m называют наибольшим значением функции у = f(x) на множестве Д(х), если:
1)во множестве Д(х) существует такая точка, что f(x0) = т
2) для любого значения х из множества Д(х) выполняется неравенство

Условия существования экстремума
Если у функции существует yнаиб,
то она ограничена сверху.
Если у функции существует yнаим, то она ограничена снизу.

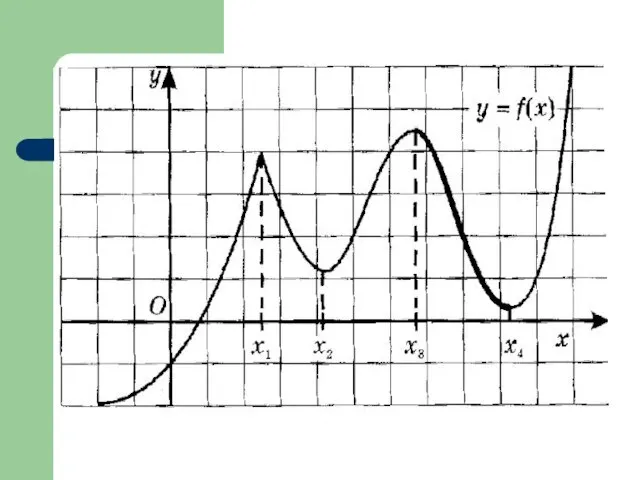
Максимум функции
Точку x0 называют точкой максимума функции у = f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство

Минимум функции
Точку x0 называют точкой минимума функции у = f(x), если у этой точки существует окрестность, для всех точек которой ( кроме самой точки x0) выполняется неравенство
Точки максимума и минимума объединяют общим названием – точки экстремума

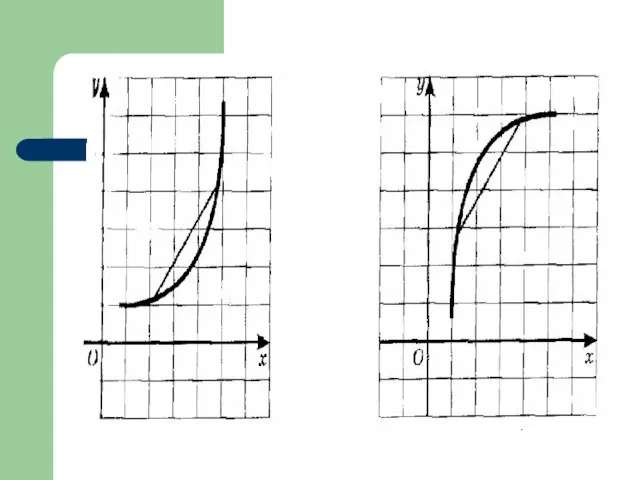
10. Выпуклость функции
Функция выпукла вниз на промежутке Д(х), если, соединив любые две точки её графика отрезком, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх на промежутке Д(х), если, соединив любые две точки её графика отрезком, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.