- Главная
- Математика
- Парадокс раздела ставки

Содержание
- 2. ИСТОРИЯ ПАРАДОКСА Этот парадокс был впервые опубликован в Венеции в 1494 г. в обзоре средневековой математики.
- 3. Как бы ни стара была проблема, фактом остается, что для ее правильного решения потребовалось очень много
- 4. СУТЬ ПАРАДОКСА Два игрока играют в честную игру (т.е. у обоих шансы победить одинаковы), и они
- 5. Согласно одному ответу, приз следовало разделить пропорционально выигранным партиям, т. е. 5:3. Тарталья предложил делить в
- 6. ОБЪЯСНЕНИЕ ПАРАДОКСА И Паскаль, и Ферма рассматривали эту проблему как задачу о вероятностях. Так что справедливым
- 8. Скачать презентацию
Слайд 2ИСТОРИЯ ПАРАДОКСА
Этот парадокс был впервые опубликован в Венеции в 1494 г. в
ИСТОРИЯ ПАРАДОКСА
Этот парадокс был впервые опубликован в Венеции в 1494 г. в

обзоре средневековой математики. Автор Лука Пачоли (1445–1509 гг.) назвал свою книгу «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности». Также Эйштейн Оре обнаружил итальянскую рукопись, датированную 1380 г., в которой также упоминается парадокс раздела ставки. Многое указывает на арабское происхождение задачи или по крайней мере на то, что в Италию задача попала вместе с арабским учением.
Слайд 3Как бы ни стара была проблема, фактом остается, что для ее правильного
Как бы ни стара была проблема, фактом остается, что для ее правильного

решения потребовалось очень много времени. Сам Пачоли даже не видел связи этой задачи с теорией вероятностей; он рассматривал ее как задачу о пропорциях.
После нескольких неудачных попыток Паскаль и Ферма в конце концов в 1654 г. независимо друг от друга нашли правильный ответ. Это открытие было настолько важным, что многие считают этот год временем рождения теории вероятностей, а все предшествующие результаты относят к ее предыстории.
После нескольких неудачных попыток Паскаль и Ферма в конце концов в 1654 г. независимо друг от друга нашли правильный ответ. Это открытие было настолько важным, что многие считают этот год временем рождения теории вероятностей, а все предшествующие результаты относят к ее предыстории.
Слайд 4СУТЬ ПАРАДОКСА
Два игрока играют в честную игру (т.е. у обоих шансы победить
СУТЬ ПАРАДОКСА
Два игрока играют в честную игру (т.е. у обоих шансы победить

одинаковы), и они договорились, что тот, кто первым выиграет 6 партий, получит весь приз. Предположим, что на самом деле игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл 5 партий, а второй – 3). Как справедливо следует разделить приз? Хотя в действительности эта проблема не является парадоксом, безуспешные попытки некоторых величайших ученых решить ее, а также неверные противоречивые ответы создали легенду о парадоксе.
Слайд 5Согласно одному ответу, приз следовало разделить пропорционально выигранным партиям, т. е. 5:3.
Согласно одному ответу, приз следовало разделить пропорционально выигранным партиям, т. е. 5:3.

Тарталья предложил делить в отношении 2:1. (Наиболее вероятно, что он рассуждал следующим образом: так как первый игрок выиграл на две партии больше, что составляет третью часть от необходимых для победы 6 партий, то первый игрок должен получить одну треть от приза, а оставшуюся часть следует разделить пополам.) На самом деле справедливым является раздел в отношении 7:1, что сильно отличается от предыдущих результатов.
Слайд 6ОБЪЯСНЕНИЕ ПАРАДОКСА
И Паскаль, и Ферма рассматривали эту проблему как задачу о вероятностях.
ОБЪЯСНЕНИЕ ПАРАДОКСА
И Паскаль, и Ферма рассматривали эту проблему как задачу о вероятностях.

Так что справедливым будет раздел, пропорциональный шансам первого игрока выиграть приз. Следуя идее Ферма, продолжим игру тремя фиктивными партиями, даже если некоторые из них окажутся лишними (т.е. когда один из игроков уже выиграл приз). Такое продолжение делает все 2*2*2 = 8 возможных исходов равновероятными. Поскольку только при одном исходе второй игрок получает приз (т.е. когда он выигрывает все три партии), а в остальных случаях побеждает первый игрок, справедливым является отношение 7:1.
Следующая -
История Герба РФ Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма
Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма Основы функционального анализа
Основы функционального анализа Алгебраические и геометрические модели
Алгебраические и геометрические модели Прямая и окружность
Прямая и окружность Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников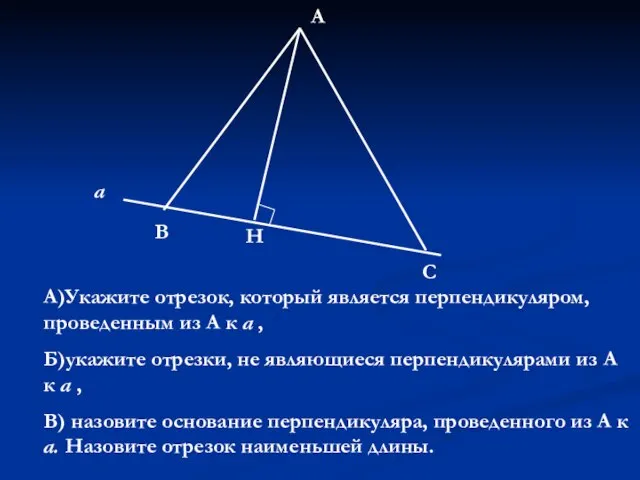 Построение треугольника
Построение треугольника Векторы. Обобщающий урок
Векторы. Обобщающий урок Решение логарифмических уравнений
Решение логарифмических уравнений Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Решение уравнений и неравенств с модулем
Решение уравнений и неравенств с модулем Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Параллелепипед. Куб
Параллелепипед. Куб Элементы комбинаторики
Элементы комбинаторики Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8
Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8 Шар и сфера
Шар и сфера Нумерация. Сложение и вычитание. Геометрические фигуры и величины
Нумерация. Сложение и вычитание. Геометрические фигуры и величины Диференціальні рівняння
Диференціальні рівняння Отрезок, луч, прямая. Графический диктант 1. 5 класс
Отрезок, луч, прямая. Графический диктант 1. 5 класс Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ
Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ  Формулы сокращенного умножения a b
Формулы сокращенного умножения a b Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок)
Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок) Дискретные случайные величины
Дискретные случайные величины Применение математики в нематематических областях
Применение математики в нематематических областях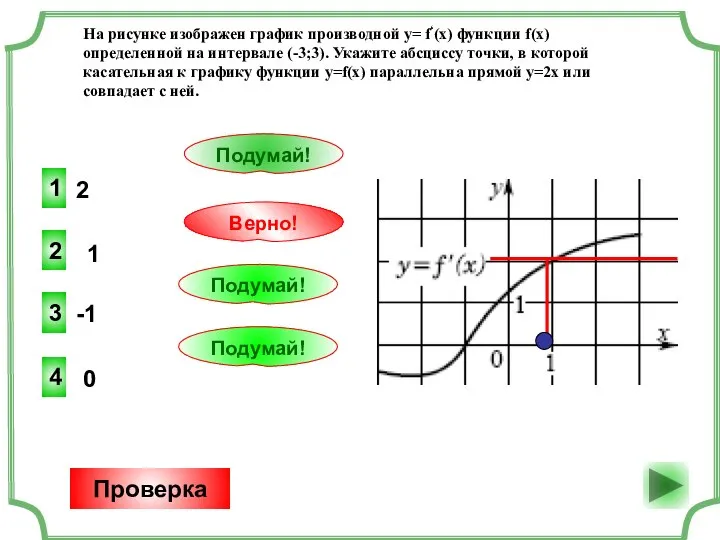 Решение задач
Решение задач Линейная функция и ее график
Линейная функция и ее график Математика (1 класс)
Математика (1 класс) Методы кластеризации
Методы кластеризации Презентация на тему Русская система мер
Презентация на тему Русская система мер