Содержание
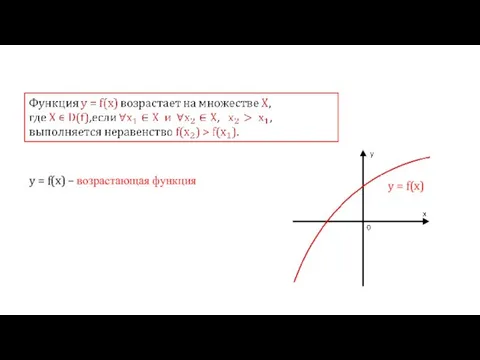
- 2. y = f(x) y = f(x) – возрастающая функция
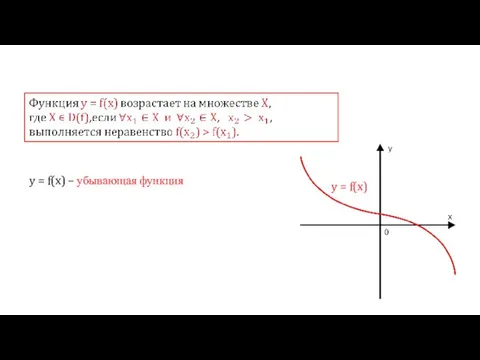
- 3. y = f(x) y = f(x) – убывающая функция
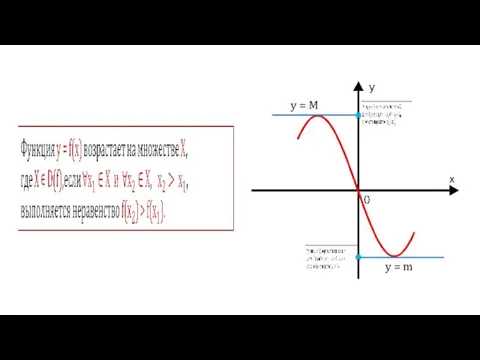
- 4. Функция у = f(х) называется монотонной на множестве Х, если она на этом промежутке или убывает
- 5. Если функция определена и непрерывна в концах интервала возрастания или убывания (а; b), то эти точки
- 6. На промежутке ( –∞;–5 ] и [ 3;+∞ ) – возрастает; на промежутке [–5;3] – убывает.
- 7. Пример. Исследовать функцию на монотонность: у = 6 – 2х. Решение. f(х) = 6 – 2х.
- 8. y = kx + b, при k > 0 y = x3 возрастающие функции, при х
- 9. Свойство 2. Ограниченность.
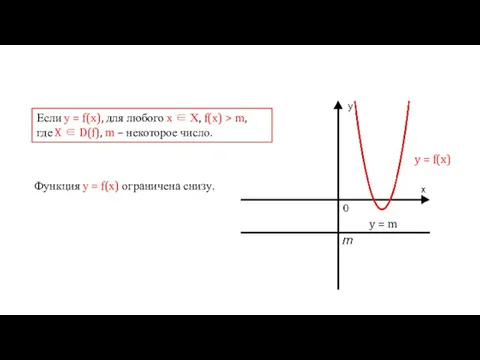
- 10. Если у = f(х), для любого х ∈ Х, f(х) > m, где X ∈ D(f),
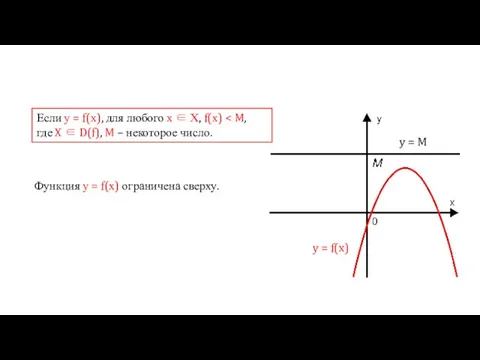
- 11. Если у = f(х), для любого х ∈ Х, f(х) где X ∈ D(f), M –
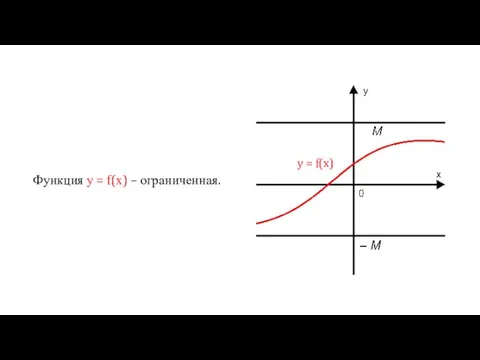
- 12. Функция у = f(х) – ограниченная. y = f(x)
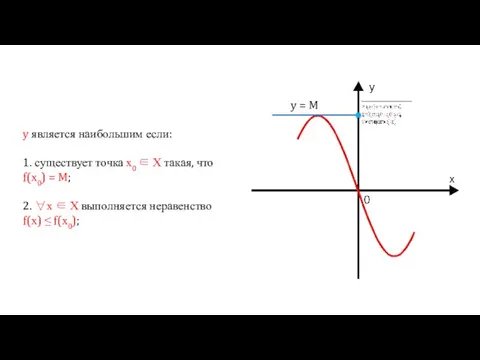
- 13. y = M y является наибольшим если: 1. существует точка х0 ∈ Х такая, что f(х0)
- 14. y = M y = m
- 15. Если у функции существует унаим. , то она ограничена снизу. Если унаиб. , то ограничена сверху.
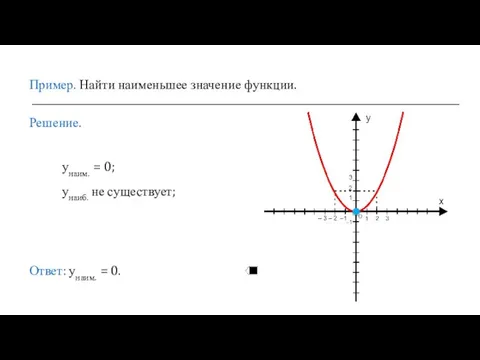
- 16. Пример. Найти наименьшее значение функции. Решение. унаим. = 0; унаиб. не существует; Ответ: унаим. = 0.
- 17. Свойство 3. Выпуклость.
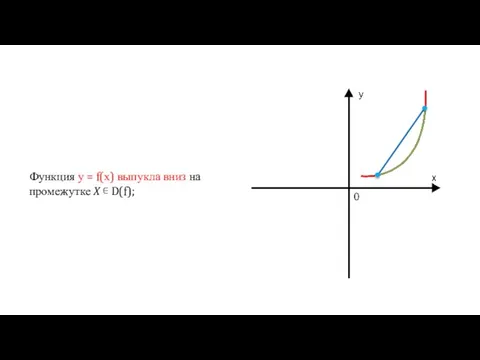
- 18. Функция у = f(х) выпукла вниз на промежутке X ∊ D(f);
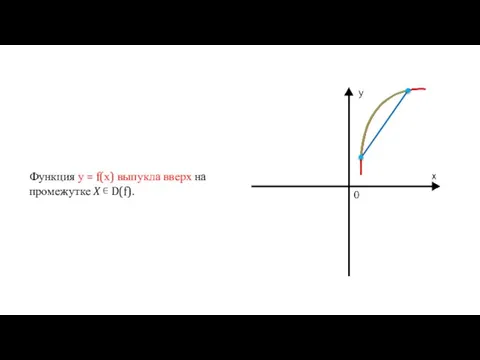
- 19. Функция у = f(х) выпукла вверх на промежутке X ∊ D(f).
- 20. Свойство 4. Непрерывность.
- 21. Функция называется непрерывной на промежутке, если она определена на этом промежутке и непрерывна в каждой точке
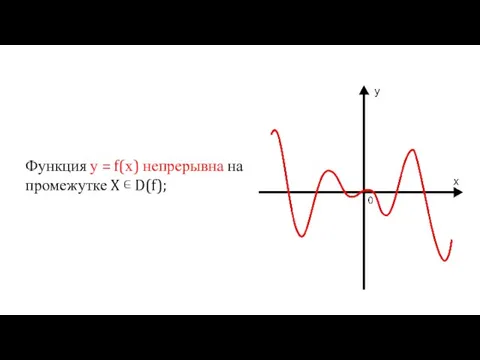
- 22. Функция у = f(х) непрерывна на промежутке X ∊ D(f);
- 23. Свойство 5. Четность, нечетность.
- 24. Если х ∊ D(f), f(–х)= f(х), то y = f(x) – четная.
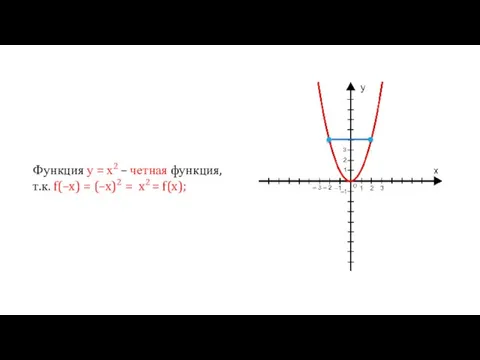
- 25. Функция у = х2 – четная функция, т.к. f(–x) = (–x)2 = x2 = f(x);
- 26. Если х ∊ D(f), f(–х)= –f(х), то у = f(x) – нечетная.
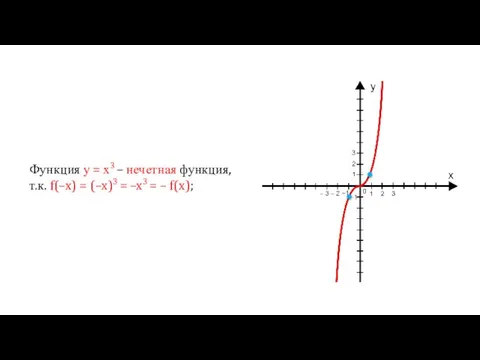
- 27. Функция у = х3 – нечетная функция, т.к. f(–x) = (–x)3 = –x3 = – f(x);
- 29. Скачать презентацию


![На промежутке ( –∞;–5 ] и [ 3;+∞ ) – возрастает; на промежутке [–5;3] – убывает.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/876487/slide-5.jpg)










 Опорная сеть памяти (ОСП) – таблица сложения
Опорная сеть памяти (ОСП) – таблица сложения Погрешности измерений
Погрешности измерений Прямоугольник. Периметр прямоугольника
Прямоугольник. Периметр прямоугольника Духовно-нравственное воспитание на уроках математики
Духовно-нравственное воспитание на уроках математики Натуральные и целые числа
Натуральные и целые числа Простейшие тригонометрические неравенства и методы их решения
Простейшие тригонометрические неравенства и методы их решения Первое знакомство с понятием вероятность. Урок 146
Первое знакомство с понятием вероятность. Урок 146 Комбинаторные задачи Тема «Введение в вероятность». Учитель Козловская Т.В. МБОУ «Хову-Аксынская СОШ»
Комбинаторные задачи Тема «Введение в вероятность». Учитель Козловская Т.В. МБОУ «Хову-Аксынская СОШ» График функции у = ах 2 + bх + qс
График функции у = ах 2 + bх + qс Презентация на тему ШАРАДЫ, МЕТАГРАММЫ, ЛОГОГРИФЫ
Презентация на тему ШАРАДЫ, МЕТАГРАММЫ, ЛОГОГРИФЫ  Matplotlib
Matplotlib Треугольники
Треугольники Скалярное произведение векторов
Скалярное произведение векторов Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия Дифференциальные уравнения в частных производных. Лекция1
Дифференциальные уравнения в частных производных. Лекция1 Дроби. Признаки делимости. Проценты. Итоговое повторение, 6 класс
Дроби. Признаки делимости. Проценты. Итоговое повторение, 6 класс Параллельность плоскостей. 10 класс
Параллельность плоскостей. 10 класс Чтение девятизначных чисел
Чтение девятизначных чисел Линейная алгебра просто! интерактивное учебное пособие
Линейная алгебра просто! интерактивное учебное пособие Способы измерения объемов геометрических тел
Способы измерения объемов геометрических тел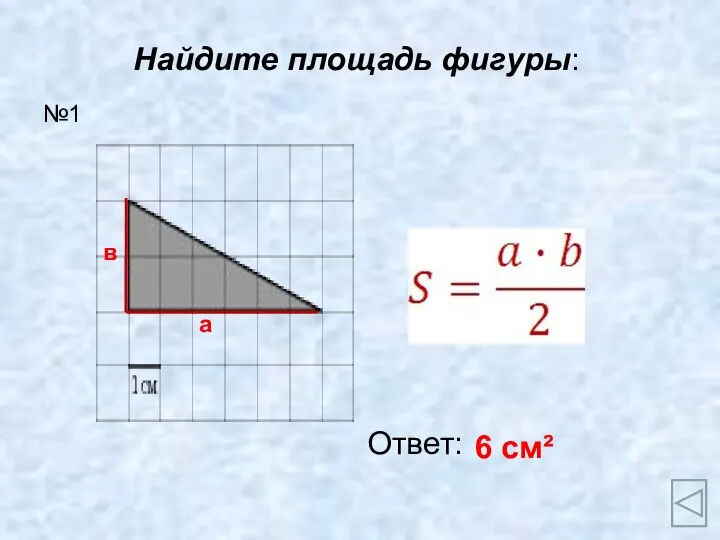 Формулы площадей
Формулы площадей Опрос общественного мнения. Повторение действий с дробями
Опрос общественного мнения. Повторение действий с дробями Занимательные задачи на смекалку
Занимательные задачи на смекалку Հետաքրքրաշարժ մաթեմատիկա 4 dasaran
Հետաքրքրաշարժ մաթեմատիկա 4 dasaran Основы моделирования
Основы моделирования Алгебра логики
Алгебра логики Задачи на проценты
Задачи на проценты