Регрессионный анализ

Регрессия (с лат. «движение назад») – функция, позволяющая по величине одного признака Х находить среднее (ожидаемое) значение другого признака У, связанного с Х корреляционно.
Регрессионный анализ — вид анализа, позволяющий выявить количественную зависимость результативного признака от одного или нескольких факторных признаков

Задача регрессионного анализа заключается в установлении формы зависимости, в определении уравнения регрессии, использование уравнения для оценки неизвестных значений зависимой переменной

Пример

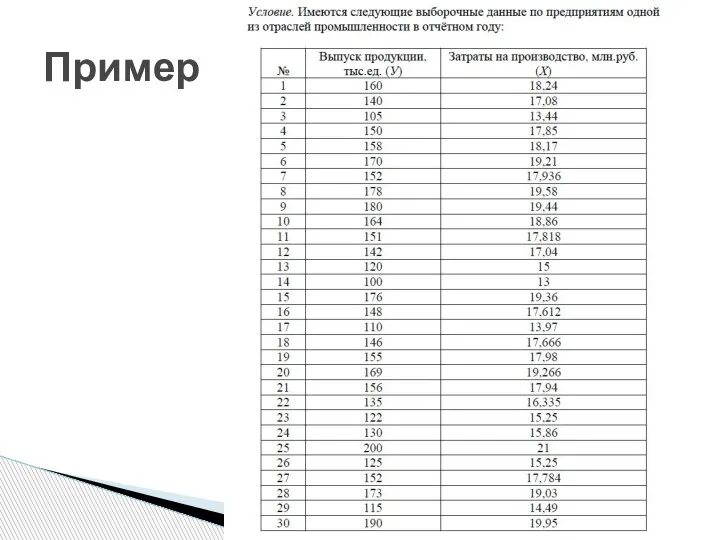
Необходимо:
найти линейное уравнение регрессии, оценив его коэффициенты методом МНК;
дать интерпретацию коэффициентов найденного уравнения;
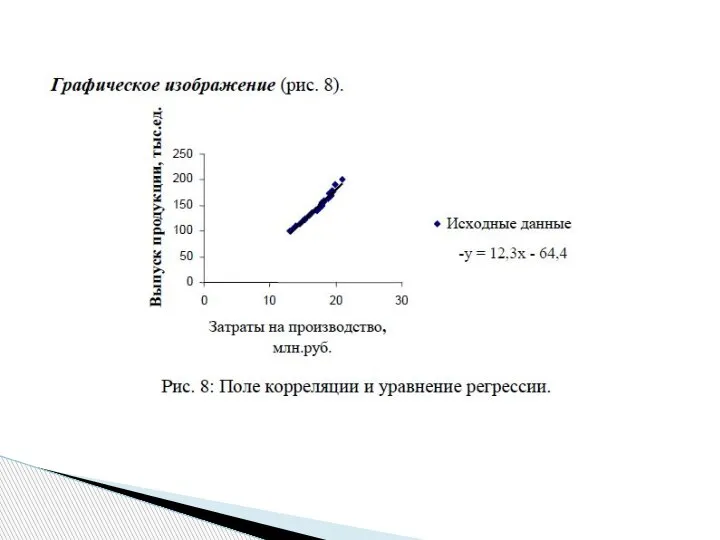
на одной координатной плоскости построить точечный график, соответствующий исходным данным, и найденную в прямую;
вычислить коэффициент эластичности;
сделать соответствующие выводы.