Дополнительные построения в трапеции при решении задач

ОСНОВНЫЕ ПОДХОДЫ К РЕШЕНИЮ ЗАДАЧ О ТРАПЕЦИЯХ:
Подобие и пропорциональность
Дополнительные построения
Трапеция и площадь
Трапеция и окружность

1. Опускание высот из концов одного основания на другое основание
2. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину
3. Проведение через середину меньшего основания прямых, параллельных боковым сторонам
4. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину
5. Продолжение боковых сторон до пересечения

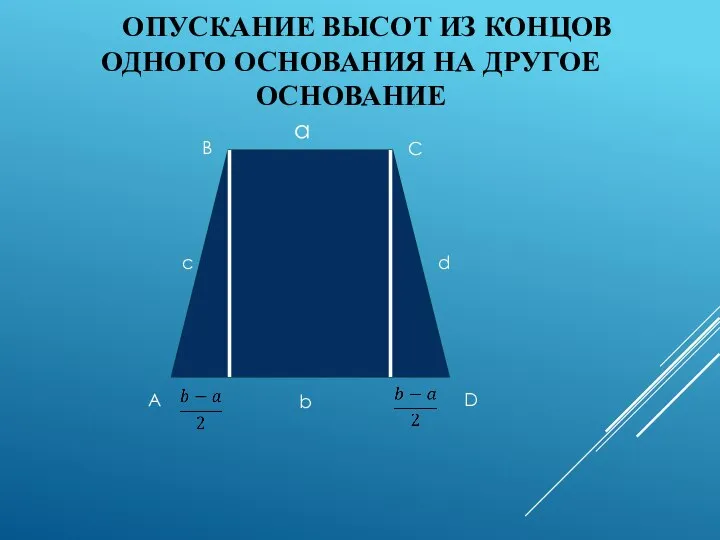
ОПУСКАНИЕ ВЫСОТ ИЗ КОНЦОВ ОДНОГО ОСНОВАНИЯ НА ДРУГОЕ ОСНОВАНИЕ
A
D
B
C
a
c
d
b

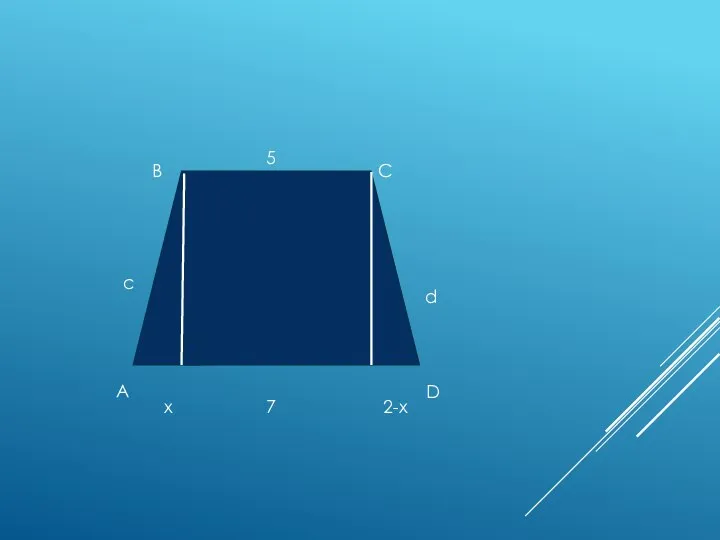
A
D
B
C
c
d
5
7
x
2-x

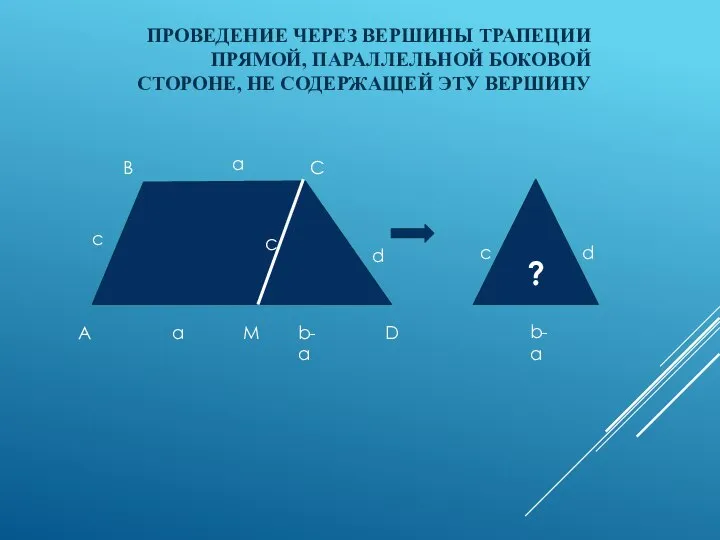
ПРОВЕДЕНИЕ ЧЕРЕЗ ВЕРШИНЫ ТРАПЕЦИИ ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ БОКОВОЙ СТОРОНЕ, НЕ СОДЕРЖАЩЕЙ ЭТУ ВЕРШИНУ
c
A
D
B
C
M
a
d
a
c
?
b-a
b-a
с
d

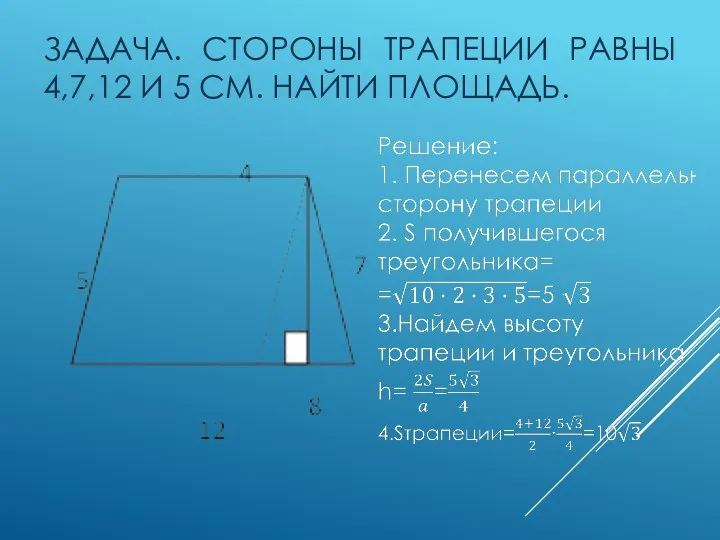
ЗАДАЧА. СТОРОНЫ ТРАПЕЦИИ РАВНЫ 4,7,12 И 5 СМ. НАЙТИ ПЛОЩАДЬ.

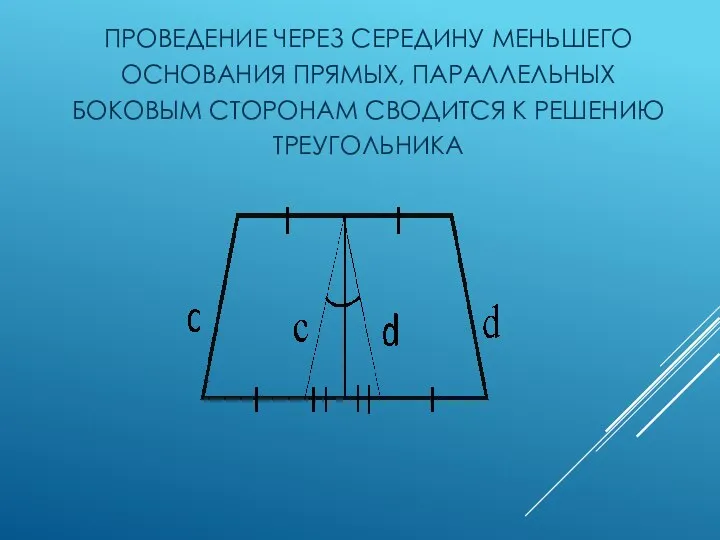
ПРОВЕДЕНИЕ ЧЕРЕЗ СЕРЕДИНУ МЕНЬШЕГО ОСНОВАНИЯ ПРЯМЫХ, ПАРАЛЛЕЛЬНЫХ БОКОВЫМ СТОРОНАМ СВОДИТСЯ К РЕШЕНИЮ ТРЕУГОЛЬНИКА

ЗАДАЧА. В ТРАПЕЦИИ СРЕДНЯЯ ЛИНИЯ РАВНА 4 СМ, УГЛЫ ПРИ ОДНОМ ИЗ ОСНОВАНИИ РАВНЫ 40º И 50º. НАЙДИТЕ ОСНОВАНИЯ ТРАПЕЦИИ, ЕСЛИ ОТРЕЗОК, СОЕДИНЯЮЩИЙ СЕРЕДИНЫ ОСНОВАНИЙ, РАВЕН 1 СМ.

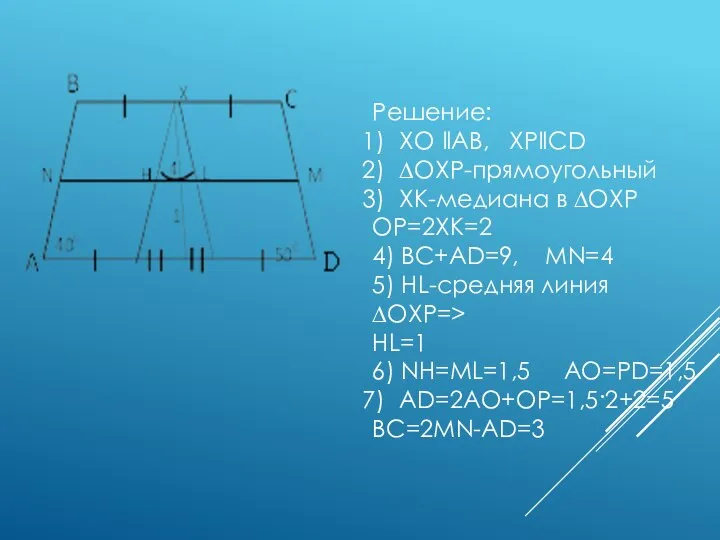
Решение:
XO ‖AB, XP‖CD
∆OXP-прямоугольный
XK-медиана в ∆OXP
OP=2XK=2
4) BC+AD=9, MN=4
5) HL-средняя линия ∆OXP=>
HL=1
6) NH=ML=1,5 AO=PD=1,5
AD=2AO+OP=1,5·2+2=5
BC=2MN-AD=3

ПРОВЕДЕНИЕ ЧЕРЕЗ СЕРЕДИНУ МЕНЬШЕГО ОСНОВАНИЯ ПРЯМЫХ, ПАРАЛЛЕЛЬНЫХ БОКОВЫМ СТОРОНАМ

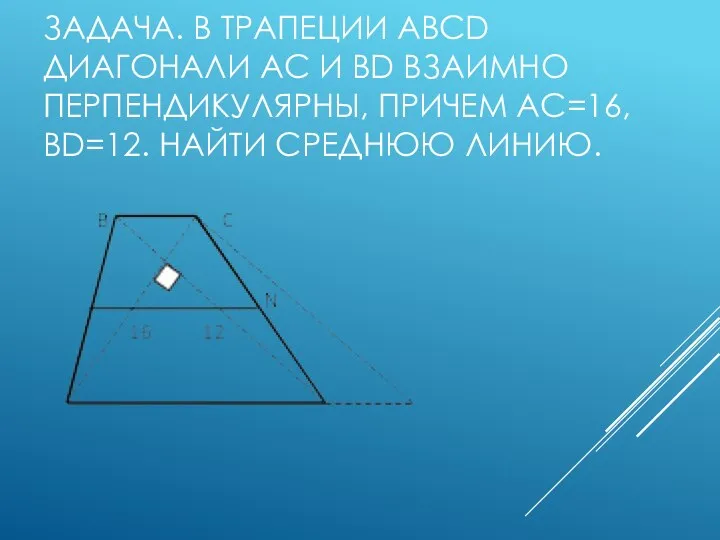
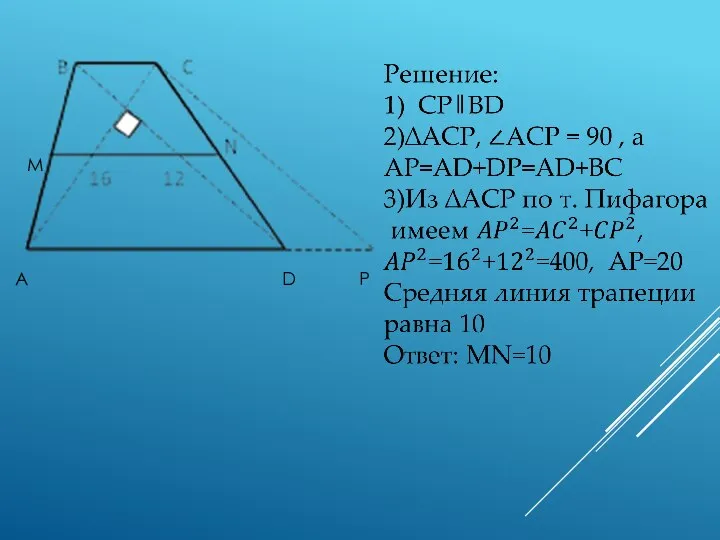
ЗАДАЧА. В ТРАПЕЦИИ ABCD ДИАГОНАЛИ AC И BD ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ, ПРИЧЕМ AC=16, BD=12. НАЙТИ СРЕДНЮЮ ЛИНИЮ.

M
A
D
P

ПРОДОЛЖЕНИЕ БОКОВЫХ СТОРОН ДО ПЕРЕСЕЧЕНИЯ

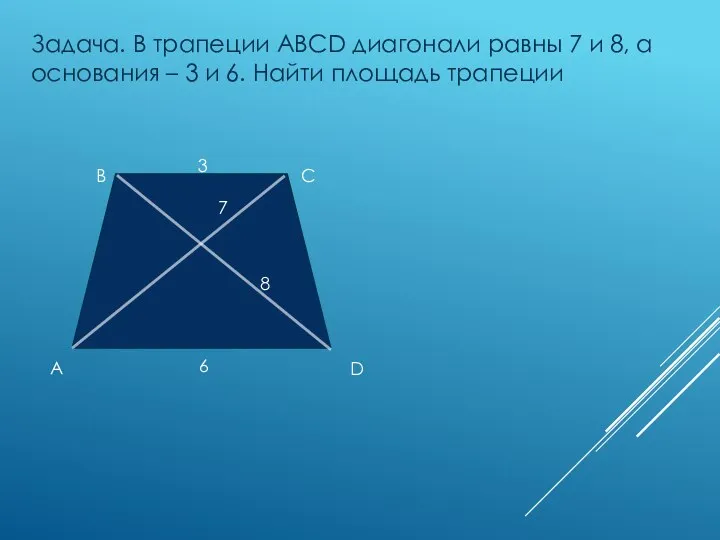
A
B
C
Задача. В трапеции ABCD диагонали равны 7 и 8, а
основания – 3 и 6. Найти площадь трапеции
D
7
8
3
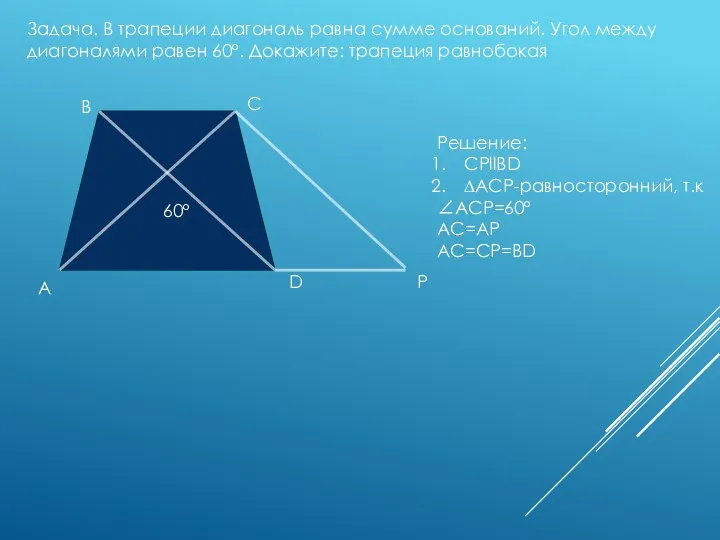
6

Задача. В трапеции диагональ равна сумме оснований. Угол между
диагоналями равен 60º. Докажите: трапеция равнобокая
60º
A
B
C
D
P
Решение:
CPllBD
∆ACP-равносторонний, т.к
∠ACP=60º
AC=AP
AC=CP=BD

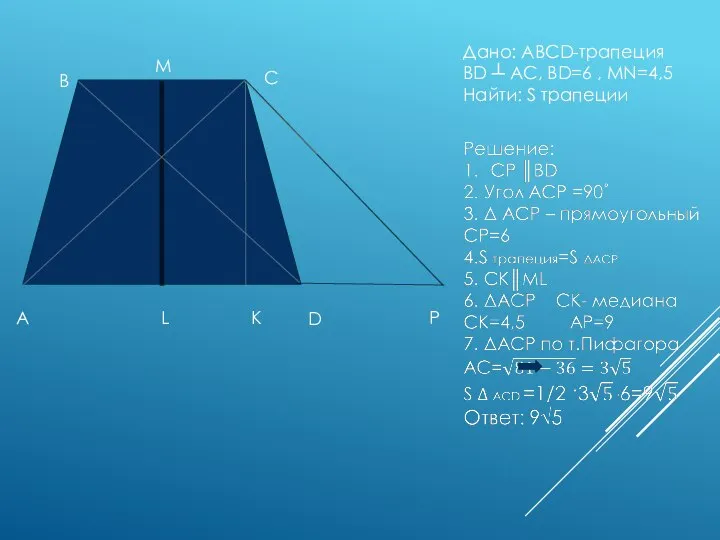
Дано: ABCD-трапеция
BD ┴ AC, BD=6 , MN=4,5
Найти: S трапеции
A
B
C
D
P
K
M
L

Вывод: Решение задач с помощью дополнительных построений не только быстрое и проще, но и намного интересней, чем решение привычными способами