Содержание
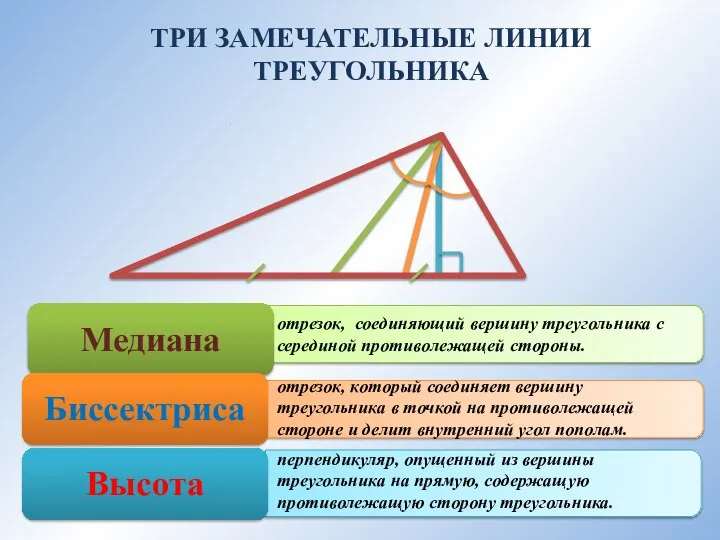
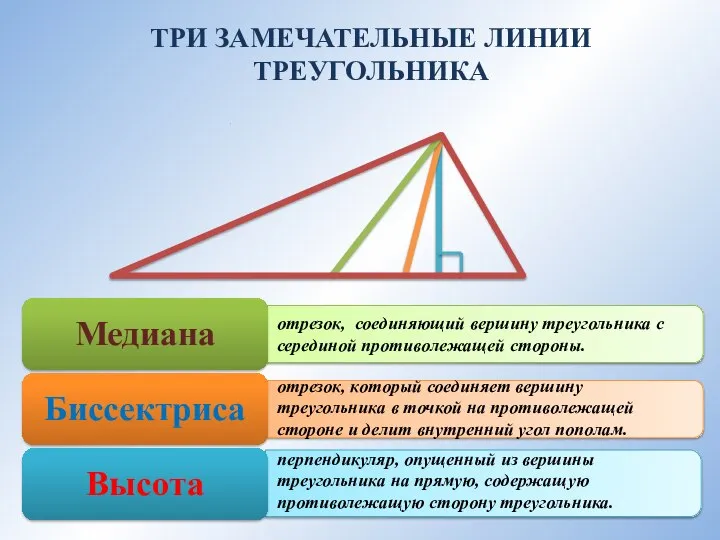
- 2. отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. отрезок, который соединяет вершину треугольника в точкой на
- 3. отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. отрезок, который соединяет вершину треугольника в точкой на
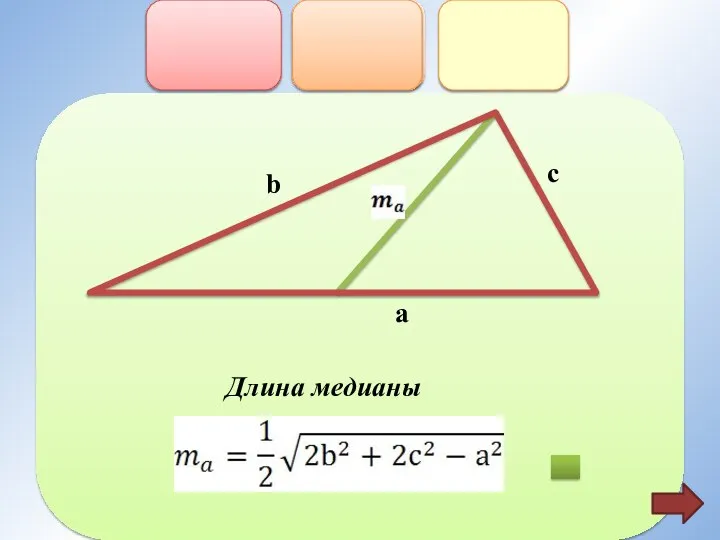
- 4. Длина медианы
- 5. b c a a1 a2 b c Три биссектрисы пересекаются в одной точке, которая всегда находится
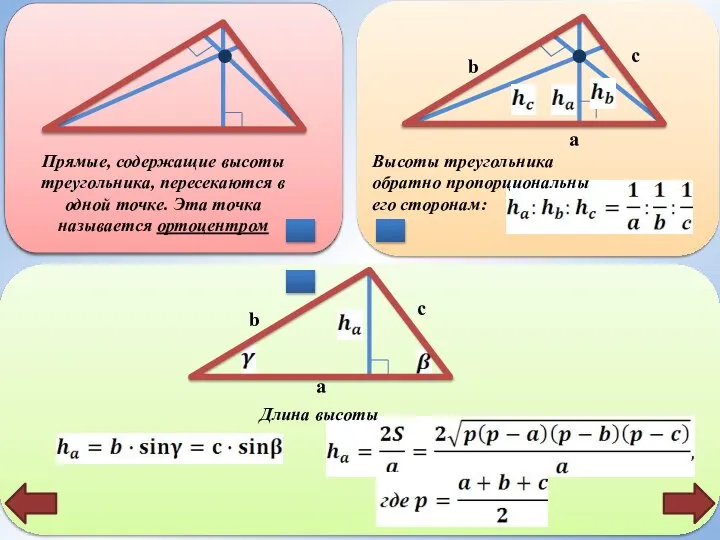
- 6. b c a b c a Прямые, содержащие высоты треугольника, пересекаются в одной точке. Эта точка
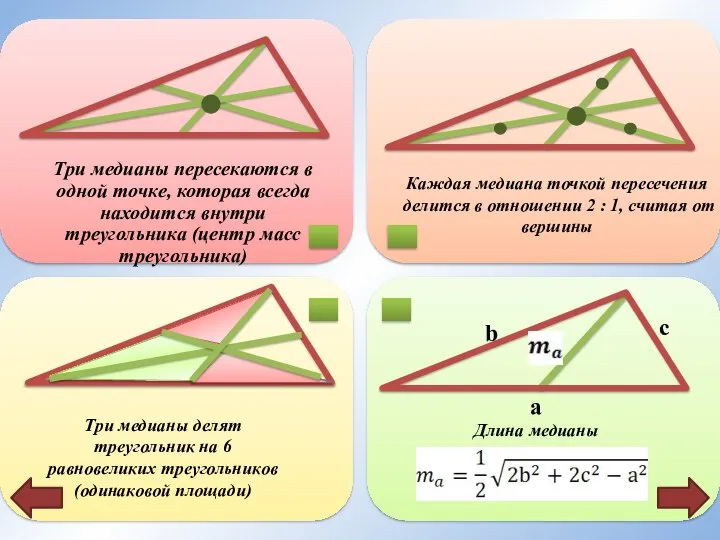
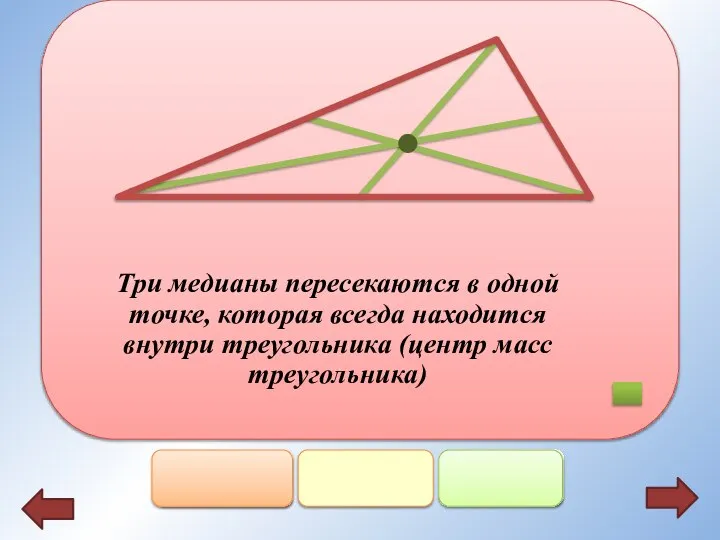
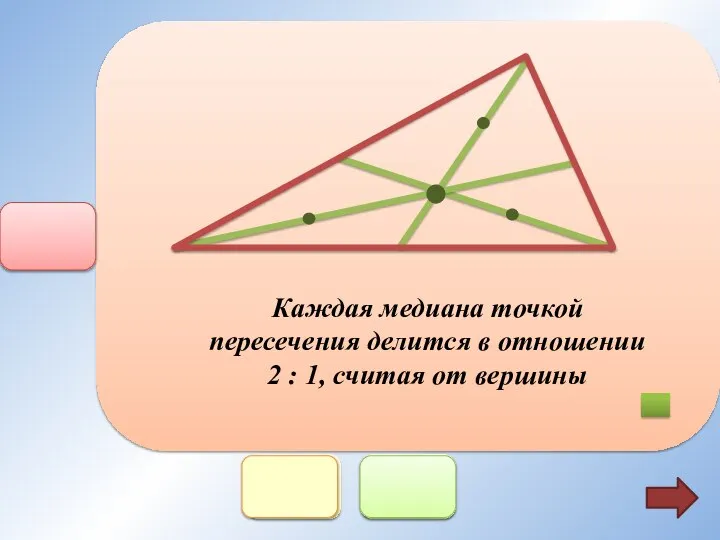
- 8. Каждая медиана точкой пересечения делится в отношении 2 : 1, считая от вершины
- 10. b c a Длина медианы
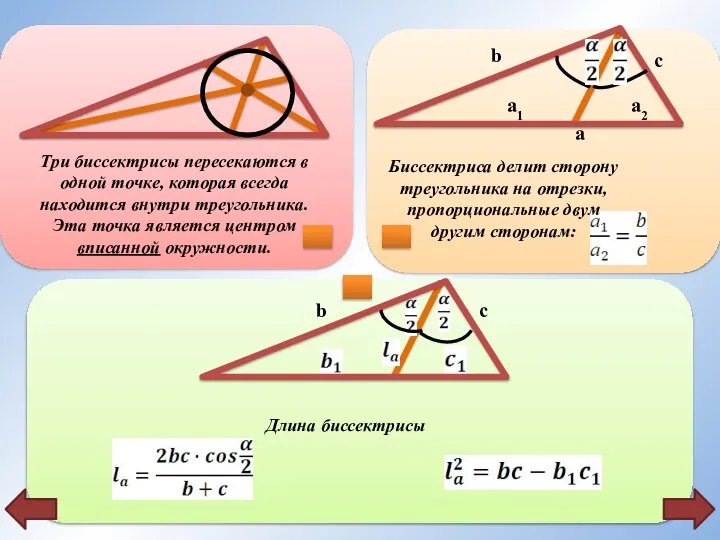
- 11. Три биссектрисы пересекаются в одной точке, которая всегда находится внутри треугольника. Эта точка является центром вписанной
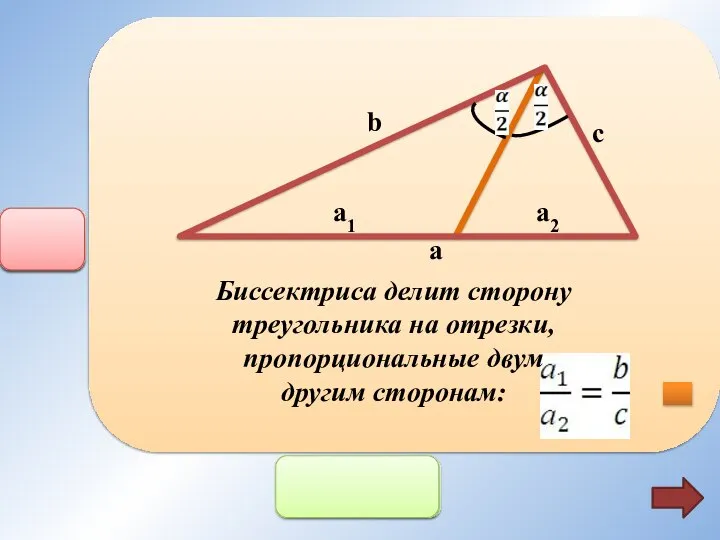
- 12. b c a a1 a2 Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим сторонам:
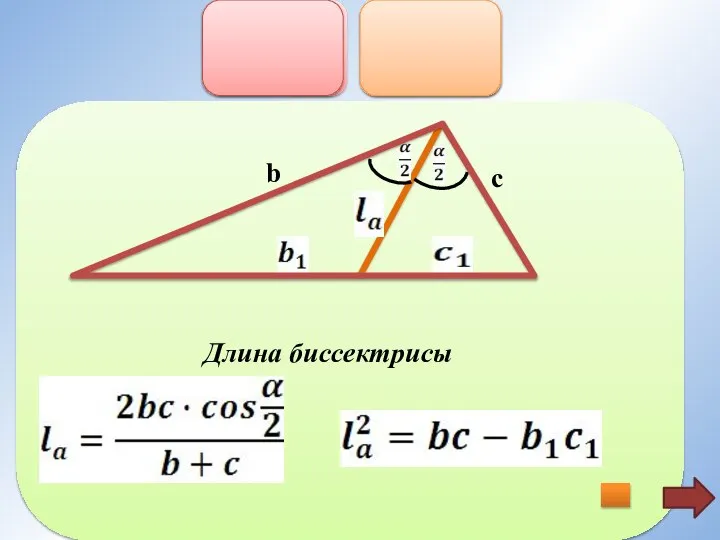
- 13. b c Длина биссектрисы
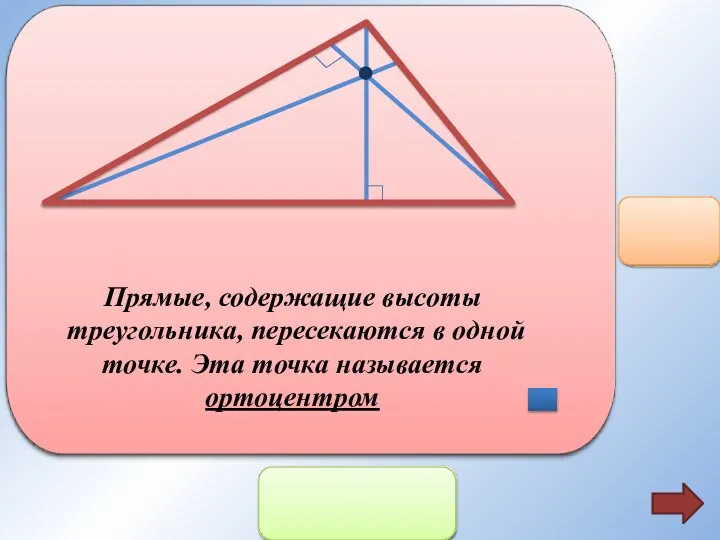
- 14. Прямые, содержащие высоты треугольника, пересекаются в одной точке. Эта точка называется ортоцентром
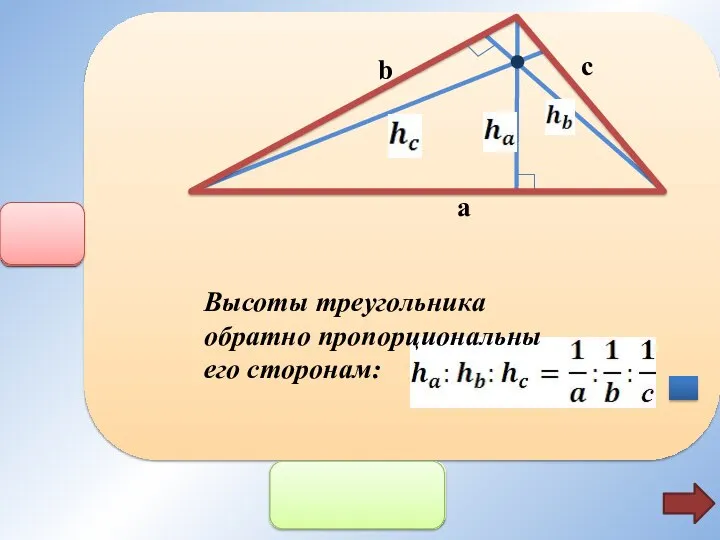
- 15. b c a Высоты треугольника обратно пропорциональны его сторонам:
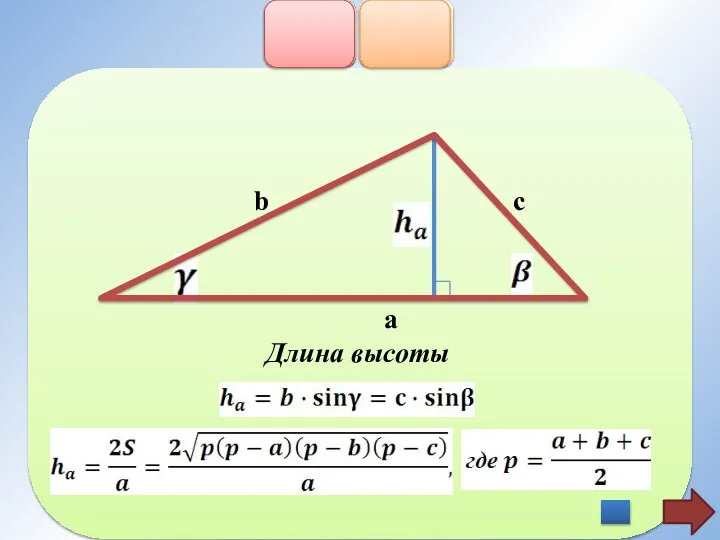
- 16. b c a Длина высоты
- 18. Скачать презентацию

 Масштаб чертежа
Масштаб чертежа Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Интегрированный урок алгебры в 8 классе
Интегрированный урок алгебры в 8 классе Презентация на тему Деление чисел
Презентация на тему Деление чисел  Matching Game
Matching Game Ringjoon, lõikaja, puutuja, kesk- ja piirdenurk. (8 klass)
Ringjoon, lõikaja, puutuja, kesk- ja piirdenurk. (8 klass) Презентация на тему Перестановка слагаемых (1 класс)
Презентация на тему Перестановка слагаемых (1 класс)  Степень числа
Степень числа Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками  Площади треугольников
Площади треугольников Декартова система координат
Декартова система координат Комплексные числа. Основные понятия
Комплексные числа. Основные понятия Подготовка к ГИА по математике. Задания 8
Подготовка к ГИА по математике. Задания 8 Математика 1 класс. Продолжение изучения связь между суммой и каждым слагаемы
Математика 1 класс. Продолжение изучения связь между суммой и каждым слагаемы Координатная плоскость
Координатная плоскость Окружность и круг
Окружность и круг Proizvodnaya_funktsii
Proizvodnaya_funktsii Математическая игра-раскраска Обезьянка
Математическая игра-раскраска Обезьянка Постройте сечения, проходящие через точки K, L, M
Постройте сечения, проходящие через точки K, L, M Математика в медицине. Области применения
Математика в медицине. Области применения Доли и дроби
Доли и дроби Математика в профессиях
Математика в профессиях Решение задач на нахождение слагаемого
Решение задач на нахождение слагаемого Среднее арифметическое в моей семье
Среднее арифметическое в моей семье Реши примеры
Реши примеры Комплексные числа
Комплексные числа Решение комбинаторных задач
Решение комбинаторных задач