- Главная
- Математика
- Теорема Пифагора

Содержание
Слайд 3Без преувеличения можно сказать, что это самая известная теорема геометрии, ибо о
Без преувеличения можно сказать, что это самая известная теорема геометрии, ибо о

ней знает подавляющее большинство населения планеты.
Теорема Пифагора
«Геометрия владеет
двумя сокровищами:
это теорема Пифагора и золотое сечение»
Иоганн Кеплер
Слайд 4Несмотря на то, что одна из основных теорем геометрии носит имя великого
Несмотря на то, что одна из основных теорем геометрии носит имя великого

Пифагора, она не была открыта самим ученым. Так, за 1500 лет до Пифагора древние Египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным и пользовались этим свойством для построения прямых углов при планировке земельных участков и сооружении зданий.
Однако именно Пифагор впервые смог доказать эту теорему и оформить ее доказательство.
Однако именно Пифагор впервые смог доказать эту теорему и оформить ее доказательство.
- Предыдущая
Повелительное наклонениеСледующая -
Творческий проект Топиарий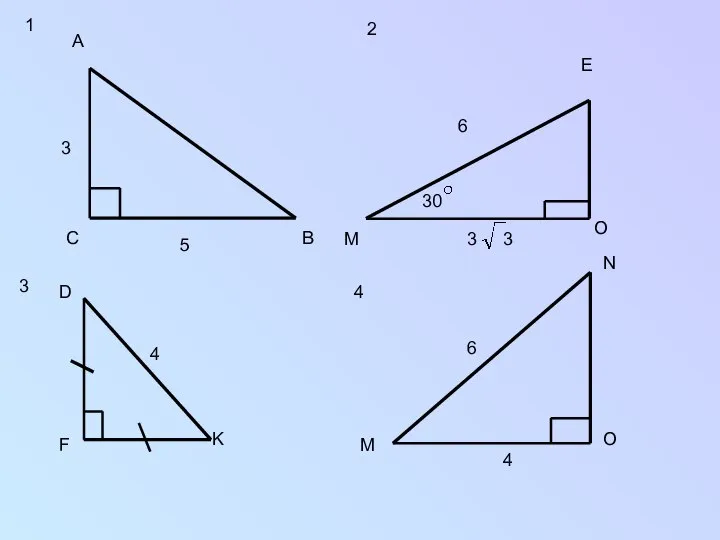
 Презентация на тему Счёт предметов (1 класс)
Презентация на тему Счёт предметов (1 класс)  Факториал
Факториал Действия со степенями. Корень n-ой степени. Степень с рациональным показателем
Действия со степенями. Корень n-ой степени. Степень с рациональным показателем Скалярное произведение векторов
Скалярное произведение векторов Таблица умножения трёх
Таблица умножения трёх Визуальный и измерительный контроль
Визуальный и измерительный контроль Погрешность средства измерений
Погрешность средства измерений Своя игра по математике
Своя игра по математике Анализ геометрических высказываний
Анализ геометрических высказываний Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Треугольник. Изображение. Обозначение
Треугольник. Изображение. Обозначение Сравниваем выражения. 2 класс
Сравниваем выражения. 2 класс Вычисление интегралов средствами MathCad
Вычисление интегралов средствами MathCad Логарифмически-нормальное (логонормальное) распределение
Логарифмически-нормальное (логонормальное) распределение Игра-тренажер Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажер Уроки с Мальвиной. Табличное умножение и деление Выполни задания в электронном дневнике
Выполни задания в электронном дневнике Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов
Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов Стереометрия. Метод координат в задачах ЕГЭ
Стереометрия. Метод координат в задачах ЕГЭ Конкурс капитанов
Конкурс капитанов Презентация на тему Округление десятичных чисел
Презентация на тему Округление десятичных чисел  Презентация на тему Показательная функция
Презентация на тему Показательная функция  Разнообразный мир линий
Разнообразный мир линий Деление дробей
Деление дробей Консультация ДУ
Консультация ДУ Выполнение плана чертежа в масштабе
Выполнение плана чертежа в масштабе ЕГЭ Профиль - Задание 6
ЕГЭ Профиль - Задание 6 тригонометрия 1 урок
тригонометрия 1 урок Основы теории вероятностей. Лекция 113
Основы теории вероятностей. Лекция 113