Содержание
- 2. Скалярное произведение векторов
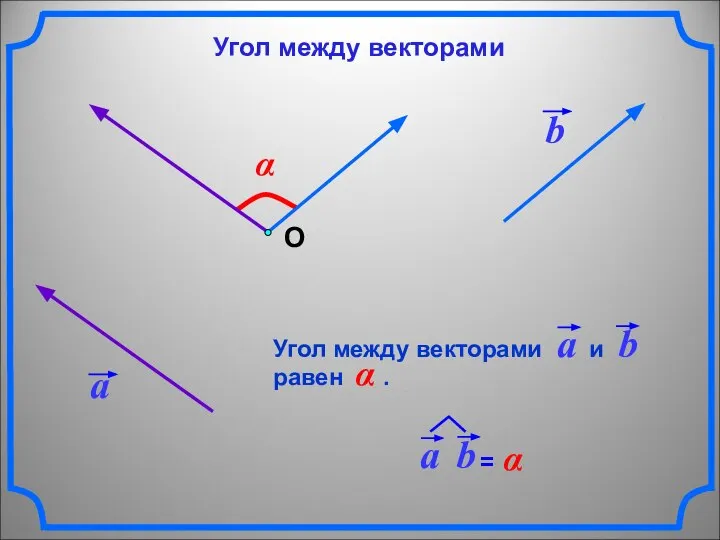
- 3. α О Угол между векторами
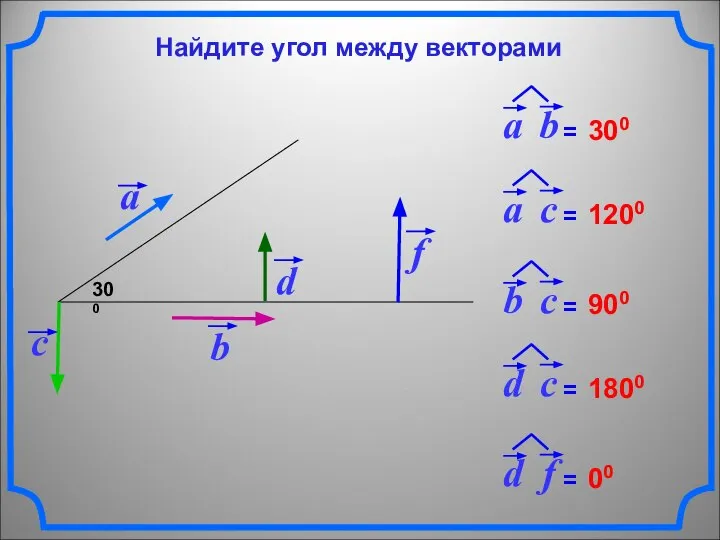
- 4. 300 300 1200 900 1800 00 Найдите угол между векторами
- 5. Скалярное произведение векторов – число (скаляр). Скалярным произведением двух векторов называется произведение их длин на косинус
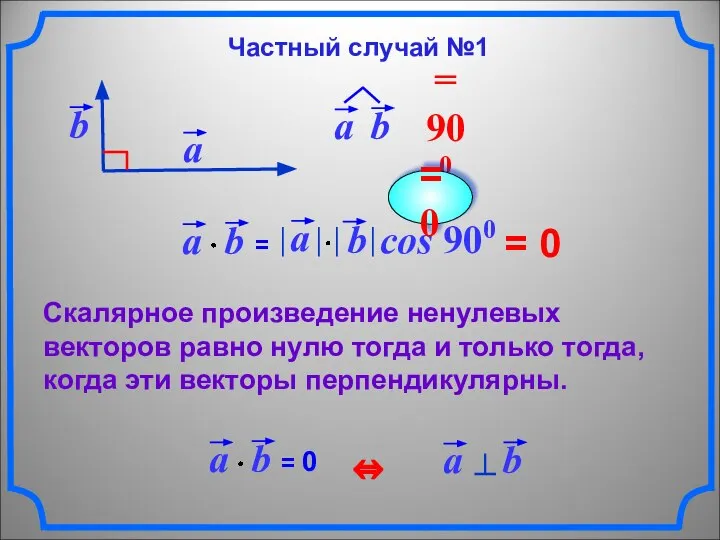
- 6. = 0 Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
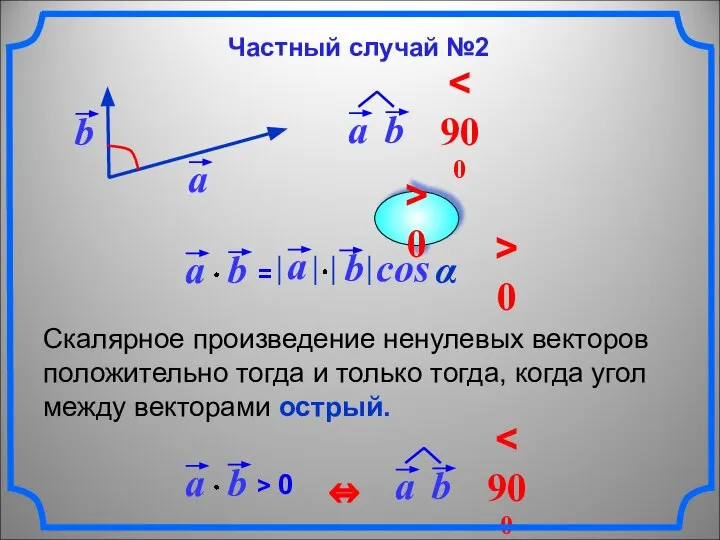
- 7. Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол между векторами острый. cos α
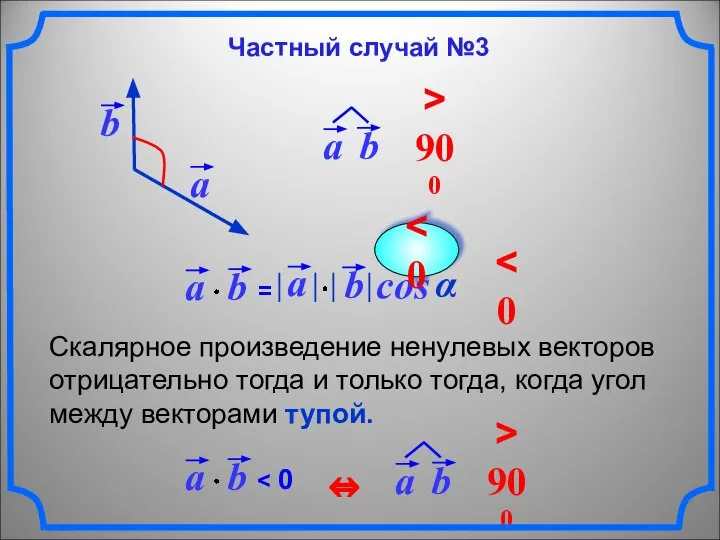
- 8. Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами тупой. cos α
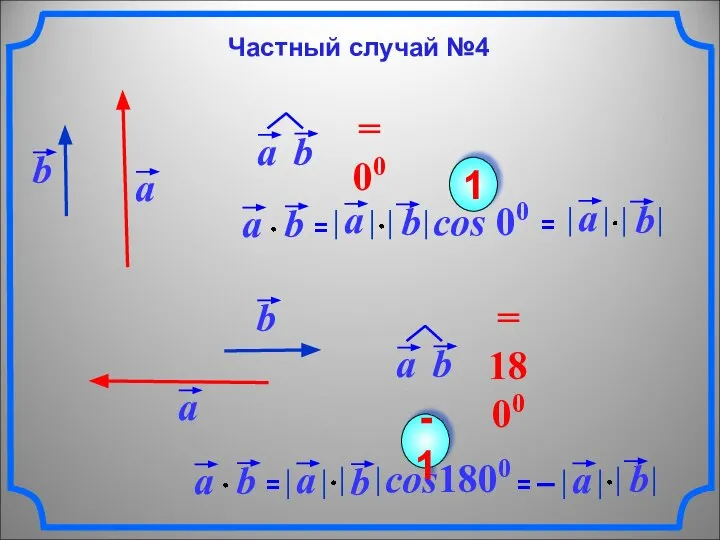
- 9. cos 00 1 cos1800 -1 Частный случай №4
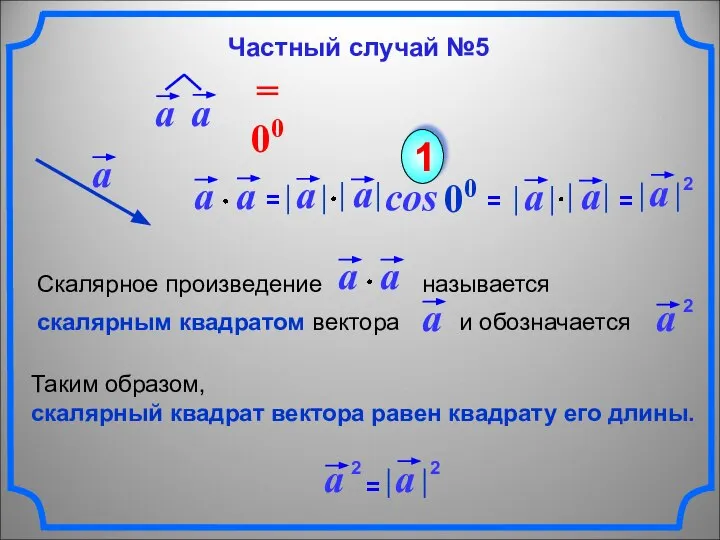
- 10. cos 00 1 Таким образом, скалярный квадрат вектора равен квадрату его длины. Частный случай №5 2
- 11. Формула для нахождения скалярного произведения через координаты векторов = x1x2 + y1y2 + z1z2
- 12. Пример №1 Найти скалярное произведение векторов: a {-6; 9; 5} b {-1; 0; 7}
- 13. Пример №2 Найти скалярное произведение векторов: a {0; 0; 4} b {22; 1; 8}
- 14. Пример №3 Найти скалярное произведение векторов: a {1; 7; 9} b {-2; 4; 0}
- 15. Скалярное произведение векторов
- 16. b {-2; 1; 3}, Найдите c {-2;-1,5; 0} = - 4 = 2,5 = 0 тупой
- 17. Косинус угла между ненулевыми векторами и выражается формулой x1 x2 + y1 y2 + z1 z2
- 18. Сочетательный закон Переместительный закон Распределительный закон 1 2 3 Свойства скалярного произведения векторов 4 причем при
- 19. Решите в тетрадях 1. Найти скалярное произведение векторов: a {1; 10; 7} b {0; 7; 0}
- 20. 2. Найти скалярное произведение векторов: a {7; 25; 0} b {11; 0; 54}
- 21. 3. Найти скалярное произведение векторов: a {-1; 2; 8} b {5; 5; 0}
- 23. Скачать презентацию













 Векторы на плоскости
Векторы на плоскости Algorytmy i struktury danych
Algorytmy i struktury danych Деление на двузначное число
Деление на двузначное число Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Решение треугольников
Решение треугольников Сложение, вычитание смешанных чисел. Задание для устного счета
Сложение, вычитание смешанных чисел. Задание для устного счета Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Методика обучения решению простых задач
Методика обучения решению простых задач Дифференцирование. Производная функции в точке
Дифференцирование. Производная функции в точке Понятие теории игр
Понятие теории игр Правила нахождения производных
Правила нахождения производных Числовые промежутки
Числовые промежутки Полимино
Полимино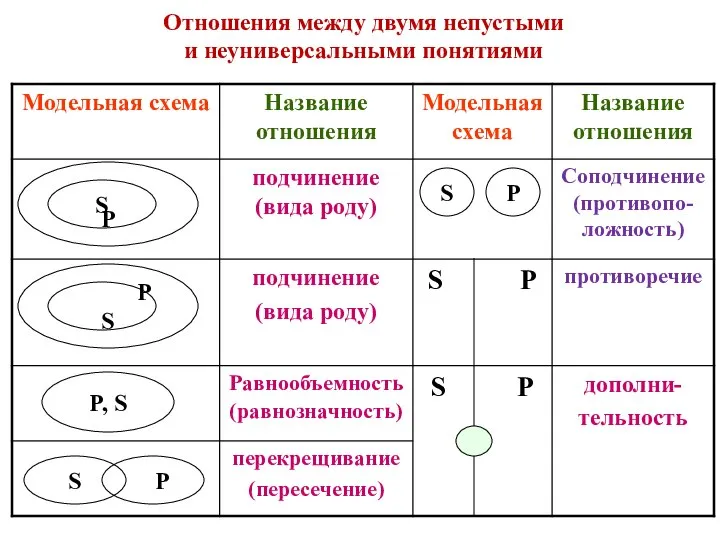 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема Математика (1 класс)
Математика (1 класс) Теорема Муавра -Лапласа
Теорема Муавра -Лапласа Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел Практико-ориентированные задачи по математике про шины
Практико-ориентированные задачи по математике про шины Проектная деятельность в школе как показатель сформированности познавательных УУД
Проектная деятельность в школе как показатель сформированности познавательных УУД SLUChAJNYE_VELIChINY
SLUChAJNYE_VELIChINY В мире магических чисел
В мире магических чисел Понятие многогранник, призма
Понятие многогранник, призма Методы решения СЛДУ
Методы решения СЛДУ Правила построения алгоритма
Правила построения алгоритма Физический смысл производной
Физический смысл производной Движение
Движение Действия над десятичными дробями
Действия над десятичными дробями Углы, связанные с окружностью
Углы, связанные с окружностью