Содержание
- 2. Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника. Тригонометрические вычисления применяются практически во
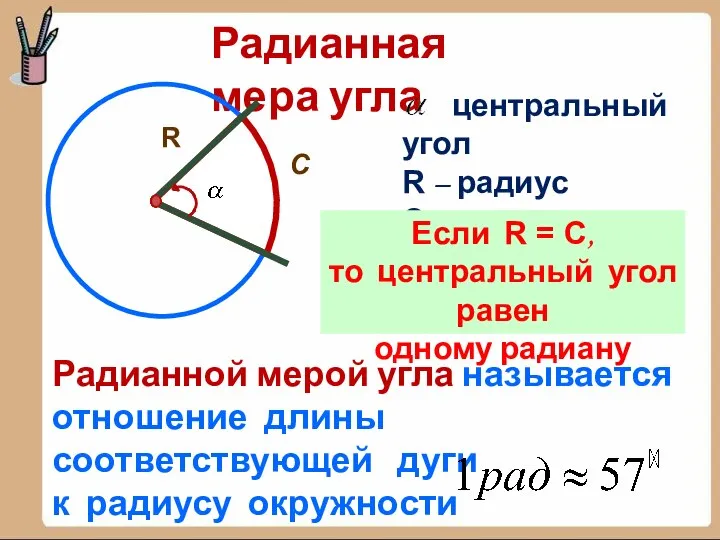
- 3. Радианная мера угла R С центральный угол R – радиус С – длина дуги Если R
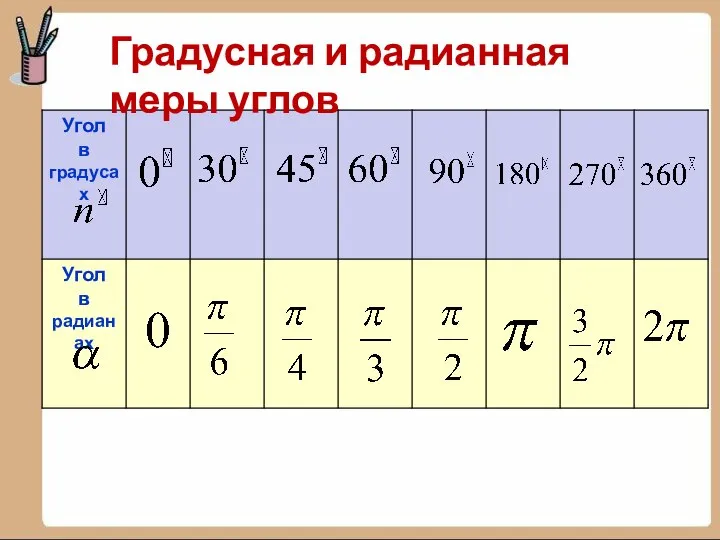
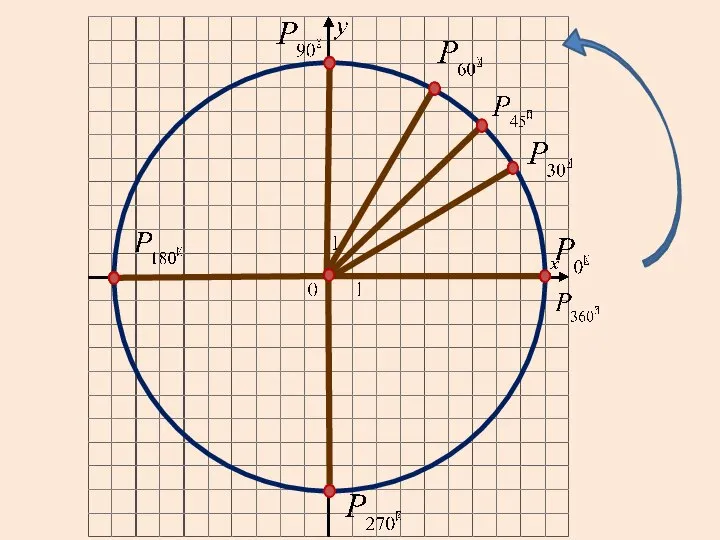
- 6. Градусная и радианная меры углов
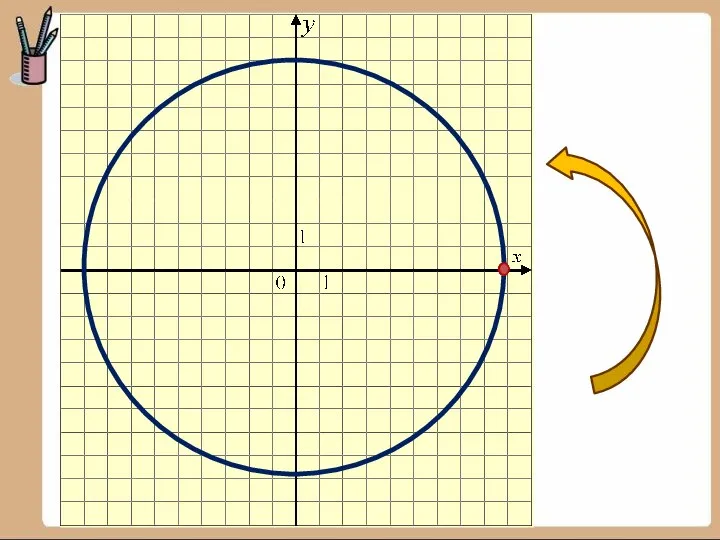
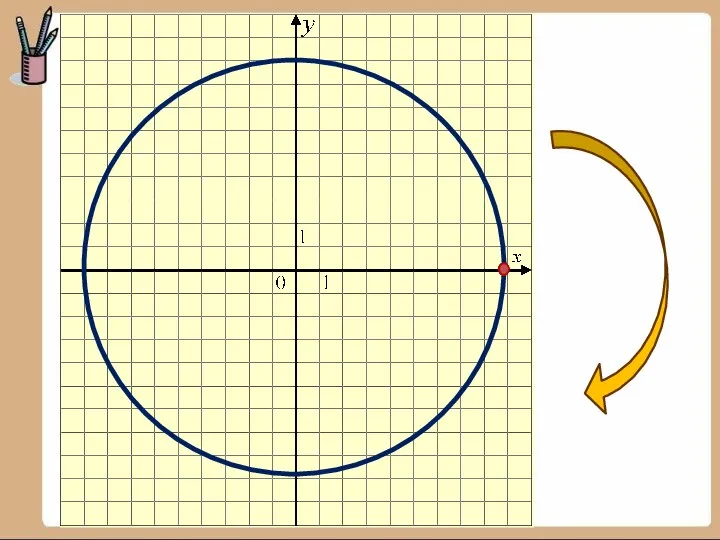
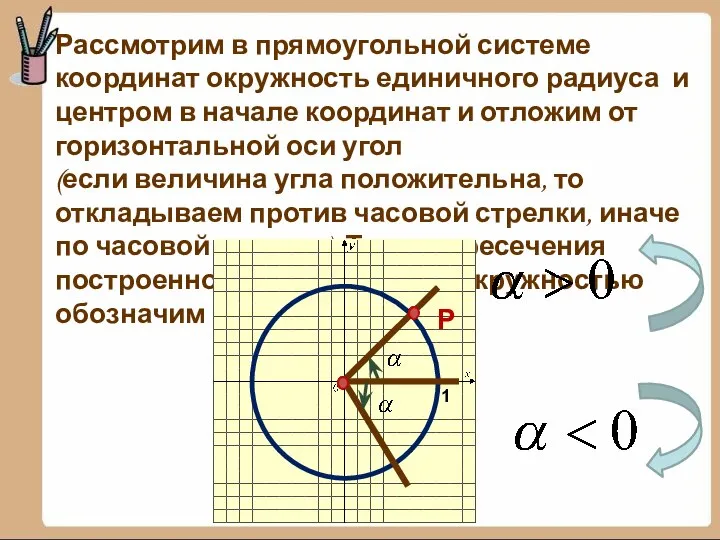
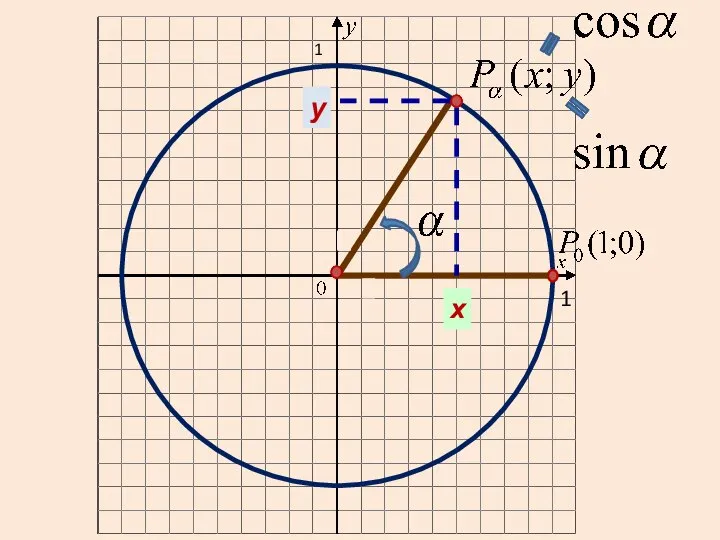
- 9. Рассмотрим в прямоугольной системе координат окружность единичного радиуса и центром в начале координат и отложим от
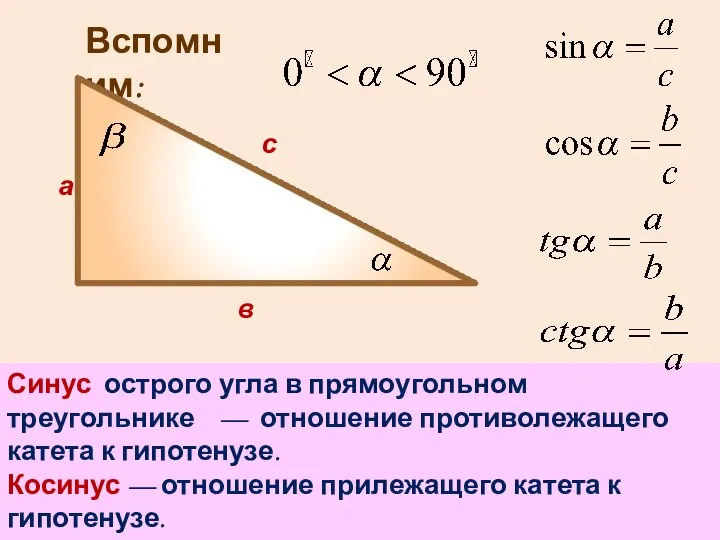
- 11. Вспомним: а в с Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе.
- 12. х у 1 1
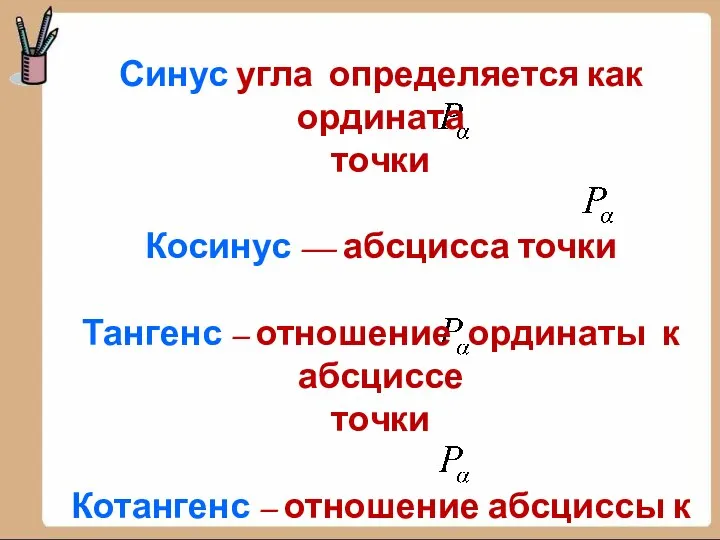
- 13. Синус угла определяется как ордината точки Косинус — абсцисса точки Тангенс – отношение ординаты к абсциссе
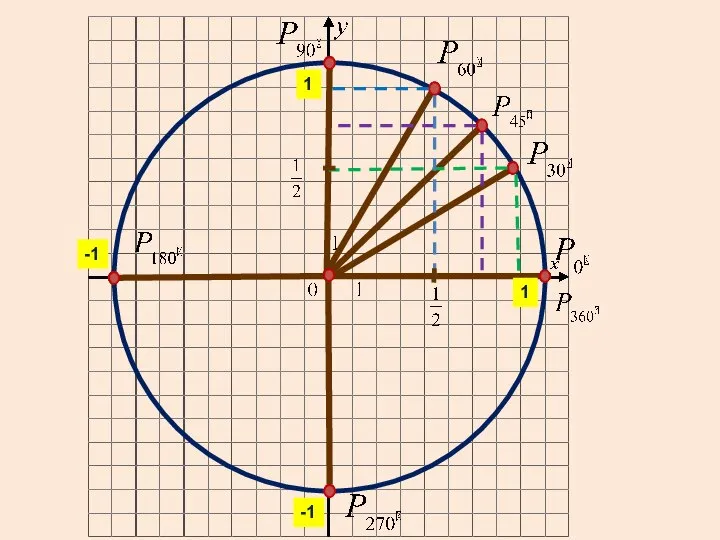
- 15. 1 1 -1 -1
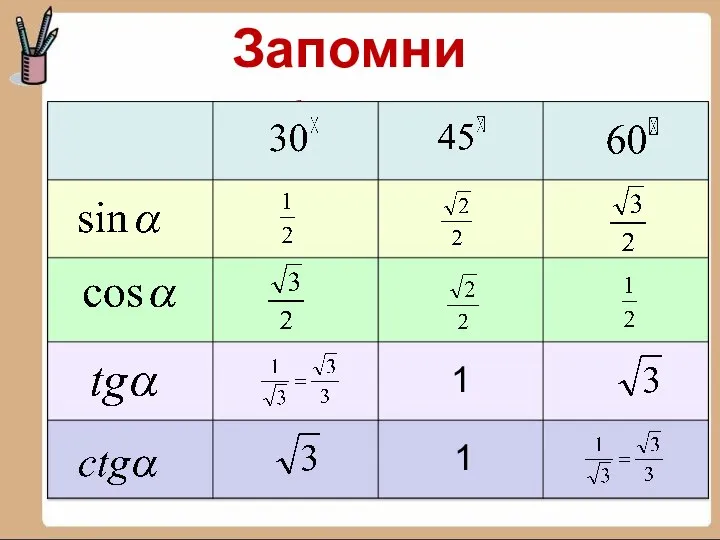
- 16. Запомним ! 1 1
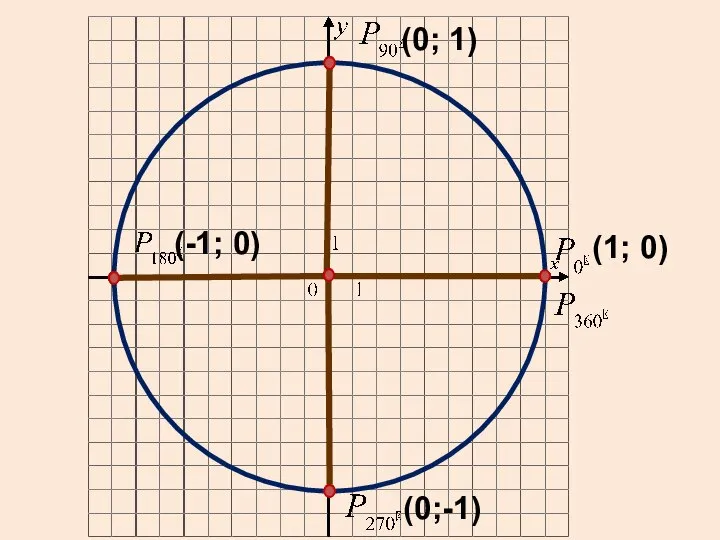
- 17. (1; 0) (0; 1) (-1; 0) (0;-1)
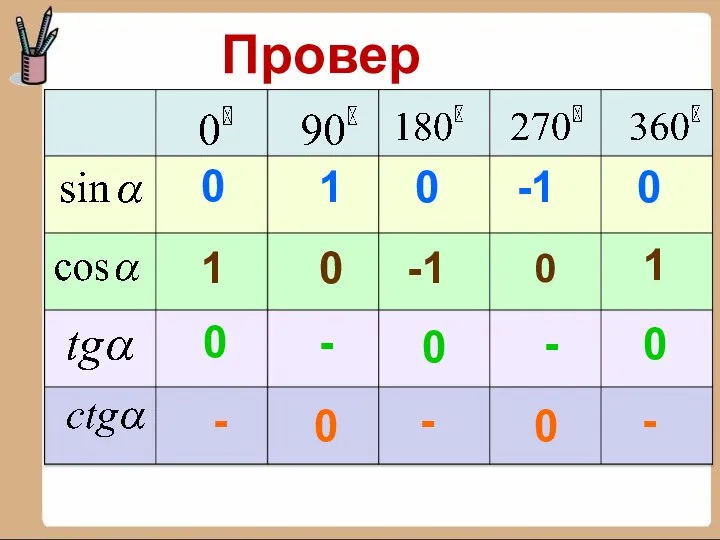
- 18. Проверим: - 0 1 0 -1 0 1 0 -1 0 1 0 0 0 0
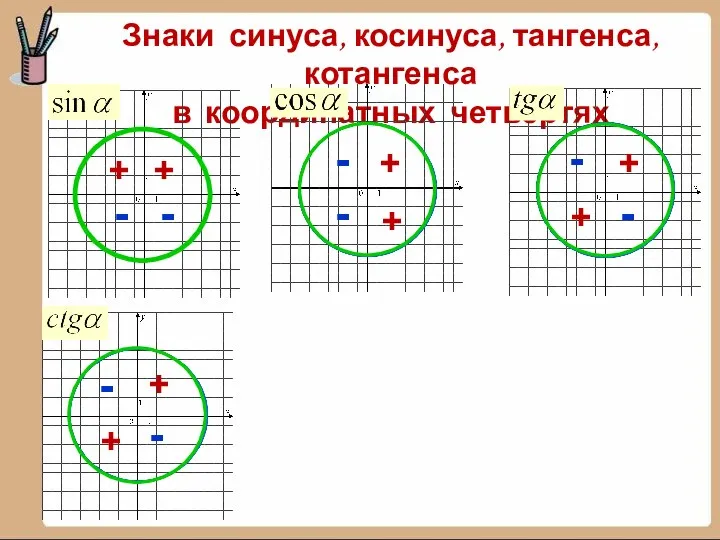
- 19. Знаки синуса, косинуса, тангенса, котангенса в координатных четвертях + + + + + + + +
- 20. Четность, нечетность синуса, косинуса, тангенса, котангенса Нечетные функции Четная функция
- 22. Скачать презентацию


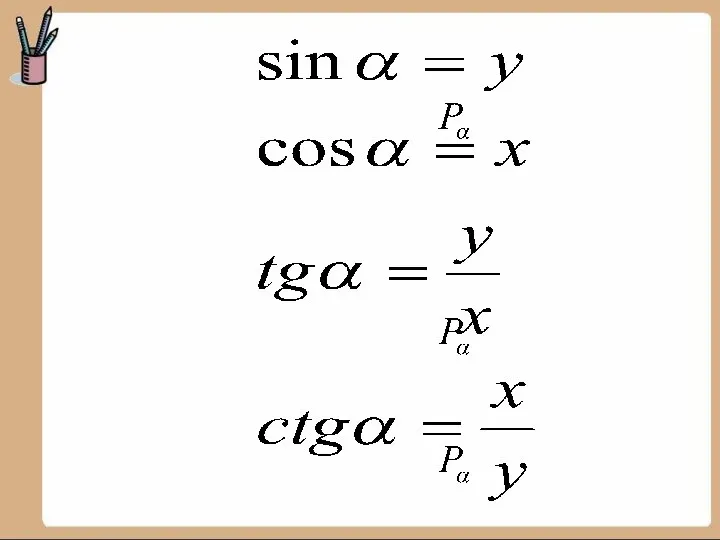

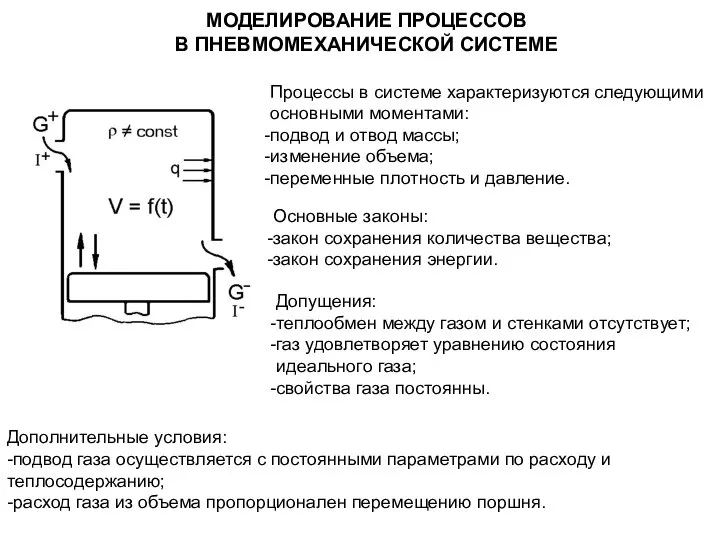 Моделирование процессов в пневмомеханической системе
Моделирование процессов в пневмомеханической системе Решение логарифмических неравенств
Решение логарифмических неравенств Теорема об интегрировании рядов Фурье
Теорема об интегрировании рядов Фурье Статистика. Необходимость возникновения статистики-науки
Статистика. Необходимость возникновения статистики-науки Состав числа в пределах 10. Тренажер
Состав числа в пределах 10. Тренажер Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Задачи на построение сечений. 10 класс
Задачи на построение сечений. 10 класс Канонические поверхности 2-го порядка
Канонические поверхности 2-го порядка Прямая и обратная пропорциональность
Прямая и обратная пропорциональность Множества и операции над ними
Множества и операции над ними Решение задач на доказательство равенства треугольников на готовых чертежах
Решение задач на доказательство равенства треугольников на готовых чертежах Угол. Виды углов. Опрос
Угол. Виды углов. Опрос Упражнения для подготовки к ОГЭ по математике, задание №8
Упражнения для подготовки к ОГЭ по математике, задание №8 Натуральный ряд
Натуральный ряд Параллельные прямые
Параллельные прямые Обеспечивающие подсистемы АИС. Математическое обеспечение
Обеспечивающие подсистемы АИС. Математическое обеспечение Теорема Пифагора (часть 2)
Теорема Пифагора (часть 2) Разные задачи (6 класс)
Разные задачи (6 класс) Развитие понятия о числе
Развитие понятия о числе Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Задачи на движение в одном направлении из одной точки
Задачи на движение в одном направлении из одной точки Пушкин и математика Выполнила ученица 10 «а» класса МОУ «Гимназия №58» г. Саратов Гаврилюк Виктория Владимировна, Регион – Сарато
Пушкин и математика Выполнила ученица 10 «а» класса МОУ «Гимназия №58» г. Саратов Гаврилюк Виктория Владимировна, Регион – Сарато Функція реакції
Функція реакції Множители и произведение
Множители и произведение Основи векторної графіки
Основи векторної графіки Геометрические фигуры
Геометрические фигуры Умножение и деление алгебраических дробей (8 класс)
Умножение и деление алгебраических дробей (8 класс) Численные методы механики сплошных сред. Индивидуальные задания
Численные методы механики сплошных сред. Индивидуальные задания