Содержание
- 2. Случайная величина X называется логарифмически-нормально распределенной, если ее логарифм подчинен нормальному закону распределения. F(x) – Функция
- 3. f(x) – Плотность распределения F(x) – Функция распределения , при μ=0
- 4. η1 = η0 + ξ1 * η0 ; η2 = η1 + ξ2 * η1 ;
- 5. (3) (4)
- 10. Основные числовые характеристики
- 12. Скачать презентацию



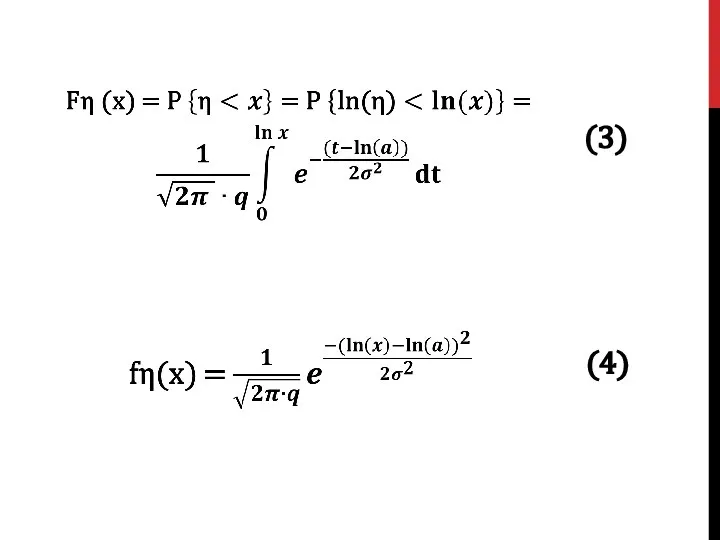





 Методы оптимизации
Методы оптимизации Решение текстовых задач
Решение текстовых задач Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)
Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)  Прямопропорциональные величины
Прямопропорциональные величины Исследование функции с помощью производной
Исследование функции с помощью производной Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Функции многих переменных
Функции многих переменных Степенная функция и ее график
Степенная функция и ее график Перевод величин
Перевод величин Площадь параллелограмма
Площадь параллелограмма Сложение в столбик
Сложение в столбик Частота и вероятность случайного события
Частота и вероятность случайного события Нахождение дроби от числа
Нахождение дроби от числа Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности
Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности Графики элементарных функций. Повторение
Графики элементарных функций. Повторение Задачи на построение
Задачи на построение Арксинус. Решение уравнения sin t = a
Арксинус. Решение уравнения sin t = a Своя игра (2)
Своя игра (2) Подобие треугольников
Подобие треугольников Задача с экологическим содержанием
Задача с экологическим содержанием Математика в карточных фокусах
Математика в карточных фокусах Сложение чисел
Сложение чисел Домашняя самостоятельная работа. 1 вариант S=16. 2 вариант S=64
Домашняя самостоятельная работа. 1 вариант S=16. 2 вариант S=64 Блиц-турнир по математике
Блиц-турнир по математике Геометрические преобразования
Геометрические преобразования Прямоугольный параллелепипед
Прямоугольный параллелепипед Հետաքրքրաշարժ մաթեմատիկա 4 dasaran
Հետաքրքրաշարժ մաթեմատիկա 4 dasaran Построение перпендикуляра и параллельных прямых
Построение перпендикуляра и параллельных прямых