Содержание
- 2. Определения
- 3. Общий план исследования двумерного распределения вероятностей Составить закон распределения вероятностей (Х,Y). Найти законы распределения и числовые
- 4. Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность совместного выполнения двух неравенств: X
- 5. Функция распределения. Свойства функции распределения 4. Если оба аргумента стремятся к + ∞, то функция распределения
- 6. Зная матрицу распределения системы двух ДСВ легко найти законы распределения отдельных случайных величин, входящих в систему:
- 7. Двумерная случайная величина {X,Y} называется непрерывной, если каждая из случайных величин X и Y является непрерывной.
- 9. Дискретные двумерные распределения вероятностей Задача Дважды бросается игральная кость. Случайные величины: Х – число появлений шестерки,
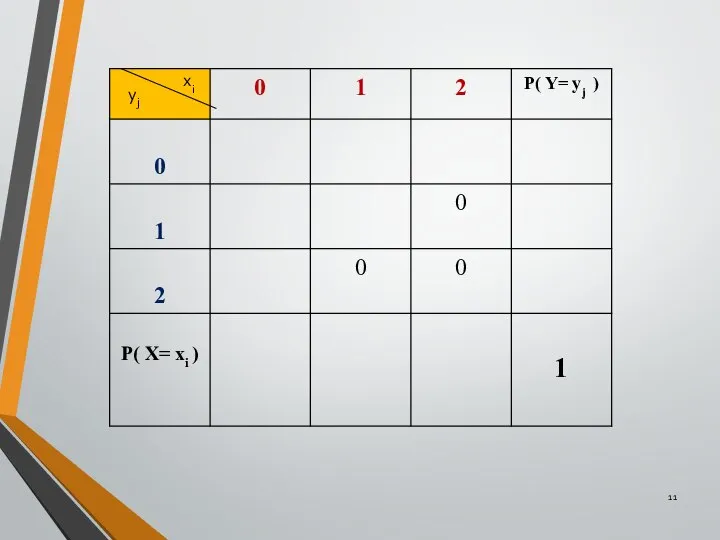
- 10. Составить закон распределения вероятностей (Х,Y): таблица распределения; функция распределения. 2. Найти законы распределения и числовые характеристики
- 11. хi yj
- 12. Установить зависимы или независимы с.в. Х и Y События A и B называются независимыми, если P(AB)
- 13. Установить зависимы или независимы с.в. Х и Y Пусть X и Y дискретные случайные величины Случайные
- 14. Ковариация и коэффициент корреляции Ковариацией (смешанный второй центральный момент, корреляционный момент) случайных величин X и Y
- 15. Свойства ковариации
- 16. Коэффициент корреляции
- 17. Коэффициент корреляции Если коэффициент корреляции равен нулю, то величины называют некоррелированными. Из независимости двух величин следует
- 18. Ковариационная и корреляционная матрицы
- 19. Регрессии величины Х на Y и величины Y на Х Условное математическое ожидание случайной величины Y
- 20. Условное распределение
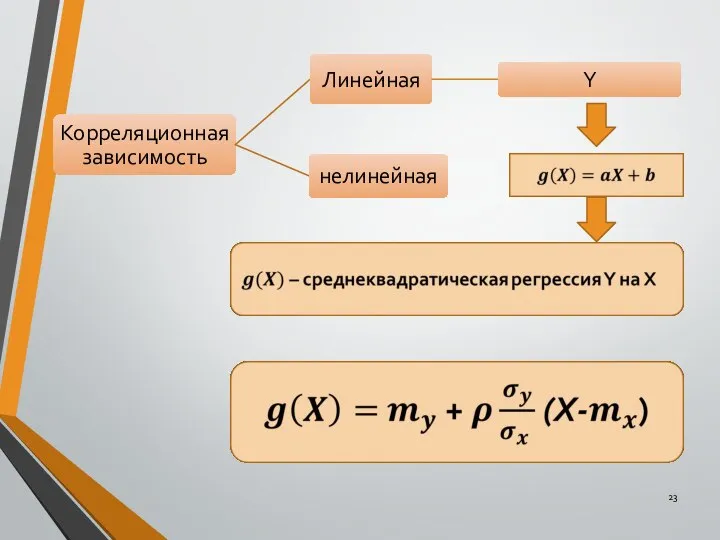
- 21. Функция регрессии
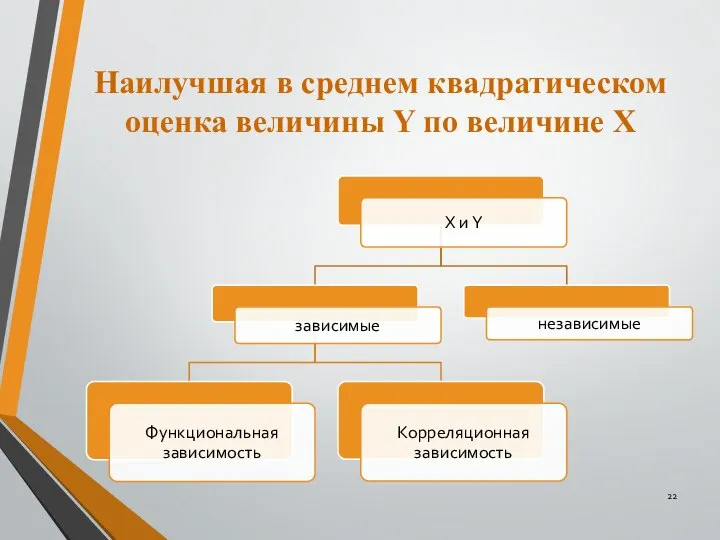
- 22. Наилучшая в среднем квадратическом оценка величины Y по величине Х
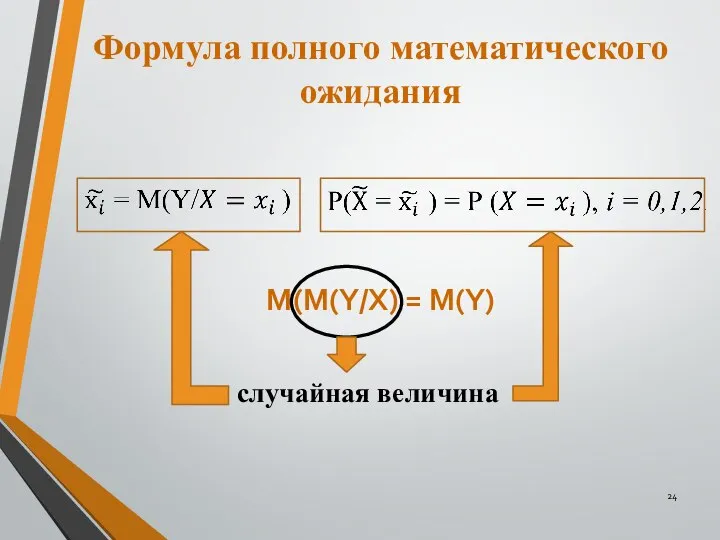
- 24. Формула полного математического ожидания М(М(Y/X) = M(Y) случайная величина
- 25. Непрерывные двумерные распределения вероятностей
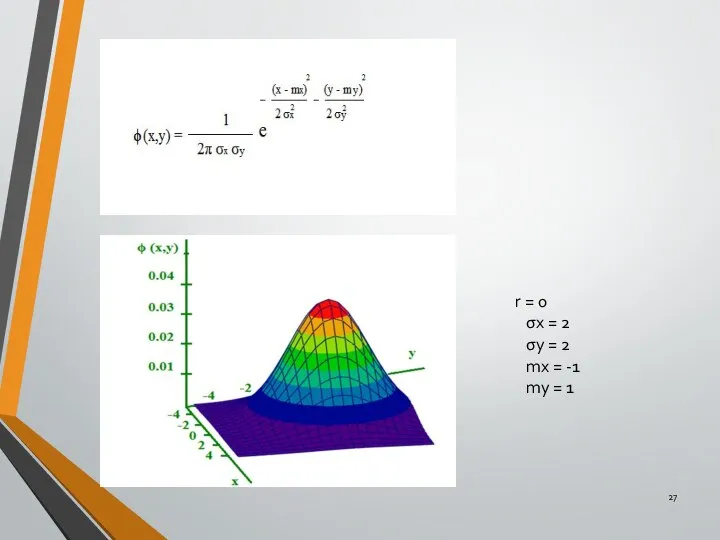
- 26. Двумерное нормальное распределение вероятностей r - коэффициент корреляции случайных величин X и Y σx - среднее
- 27. r = 0 σx = 2 σy = 2 mx = -1 my = 1
- 29. Скачать презентацию






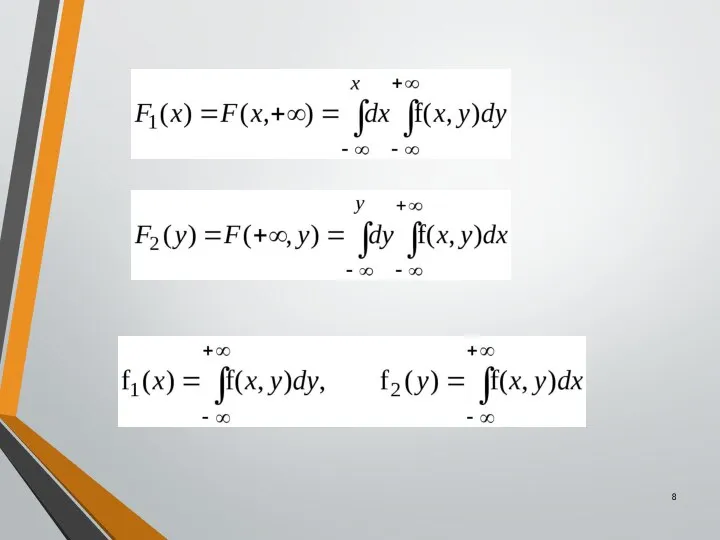














 Презентация на тему Решение систем неравенств (9 класс)
Презентация на тему Решение систем неравенств (9 класс)  Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А.
Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45 Математический диктант. Классная работа
Математический диктант. Классная работа Прямоугольник, его свойства и признаки
Прямоугольник, его свойства и признаки Производная функция
Производная функция Числа от 1 до 5. Состав числа 5
Числа от 1 до 5. Состав числа 5 Решение задач. 10 класс
Решение задач. 10 класс Производная степенной функции
Производная степенной функции Решение задач с помощью уравнений. Сказка
Решение задач с помощью уравнений. Сказка Координатные векторы
Координатные векторы Свойства матриц. Действия с матрицами
Свойства матриц. Действия с матрицами Статистические и аналитические методы оцеки рисков
Статистические и аналитические методы оцеки рисков Работа над ошибками
Работа над ошибками Счет в пределах 5
Счет в пределах 5 Статистические таблицы и графики
Статистические таблицы и графики Презентация на тему Зачем нужна математика
Презентация на тему Зачем нужна математика  Смежные и вертикальные углы
Смежные и вертикальные углы Домашнее задание. Примеры и уравнения
Домашнее задание. Примеры и уравнения Группировка слагаемых
Группировка слагаемых Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ  Теорема Пифагора
Теорема Пифагора Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Провешивание прямой на местности
Провешивание прямой на местности Лекция №3
Лекция №3 Ряды Фурье. Лекция 3.10
Ряды Фурье. Лекция 3.10 Единицы счёта
Единицы счёта Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника
Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника