Содержание
- 2. Результат теста Верно: 14 Ошибки: 0 Отметка: 5 Время: 1 мин. 51 сек. ещё
- 3. Вариант 2 а) V=S∙ℓ∙cos? в) V=S∙ℓ∙tg? б) V=S∙ℓ∙sin? 1. Боковое ребро наклонной призмы длиной ℓ составляет
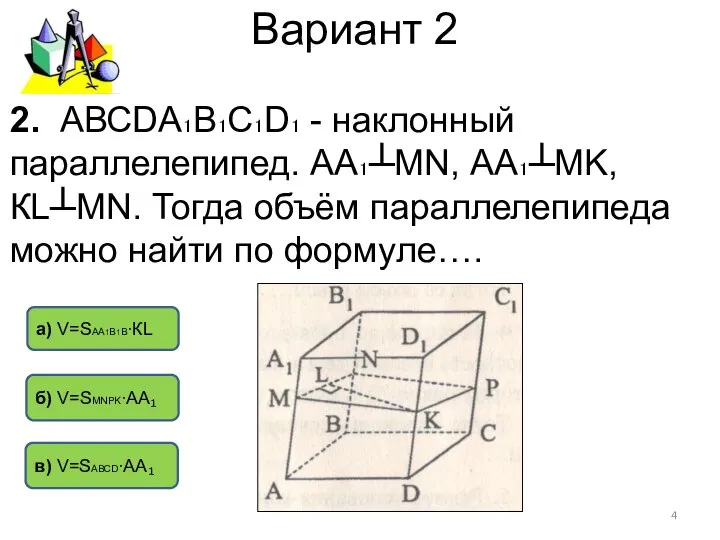
- 4. Вариант 2 б) V=SМNPK∙АА₁ а) V=SАА1В1В∙КL в) V=SАВСD∙АА₁ 2. АВСDА₁В₁С₁D₁ - наклонный параллелепипед. АА₁┴MN, АА₁┴MK, КL┴MN.
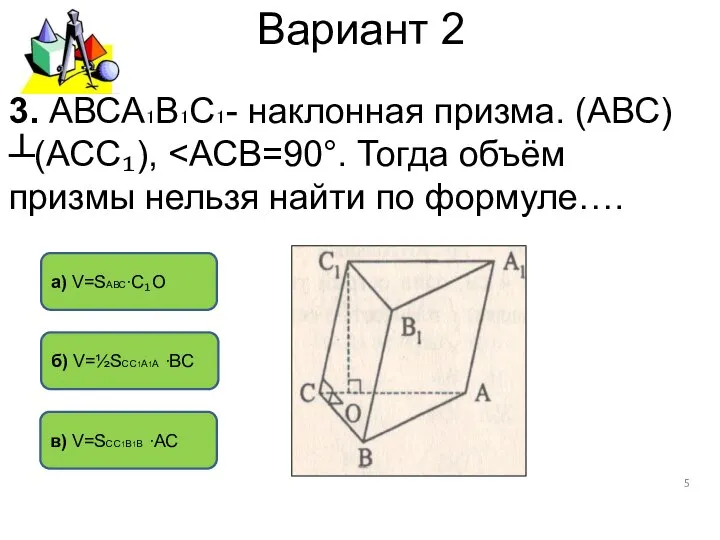
- 5. Вариант 2 в) V=SСС1В1В ∙АС а) V=SАВС∙С₁О б) V=½SСС1А1А ∙ВС 3. АВСА₁В₁С₁- наклонная призма. (АВС)┴(АСС₁),
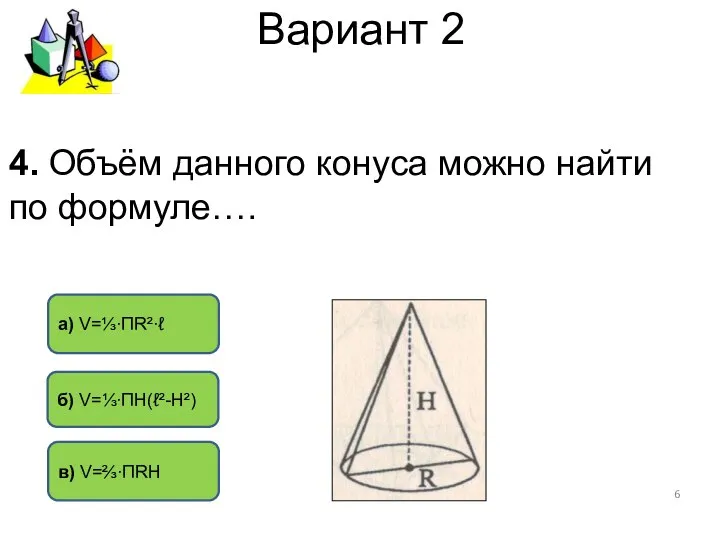
- 6. Вариант 2 б) V=⅓∙ПH(ℓ²-H²) в) V=⅔∙ПRH а) V=⅓∙ПR²∙ℓ 4. Объём данного конуса можно найти по формуле….
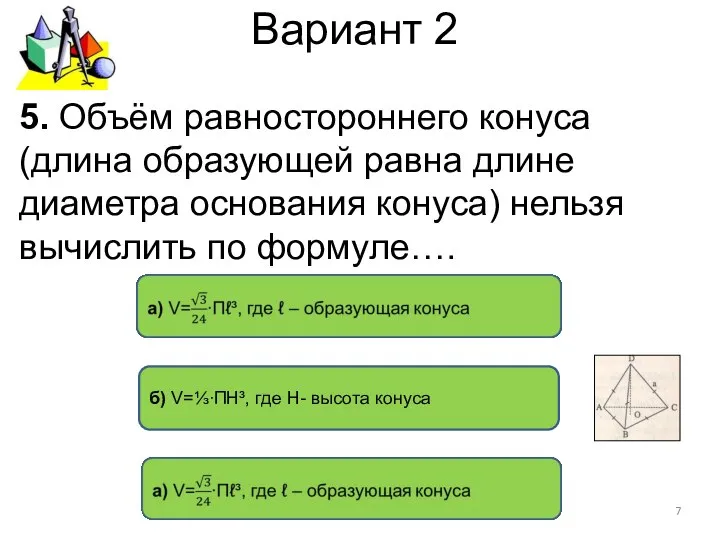
- 7. Вариант 2 б) V=⅓∙ПН³, где Н- высота конуса 5. Объём равностороннего конуса (длина образующей равна длине
- 8. Вариант 2 в) V=1/6∙Н(d₁²+d₂²+d₁d₂), где d₁ и d₂ - диаметры оснований 6. Объём усеченного конуса, высота
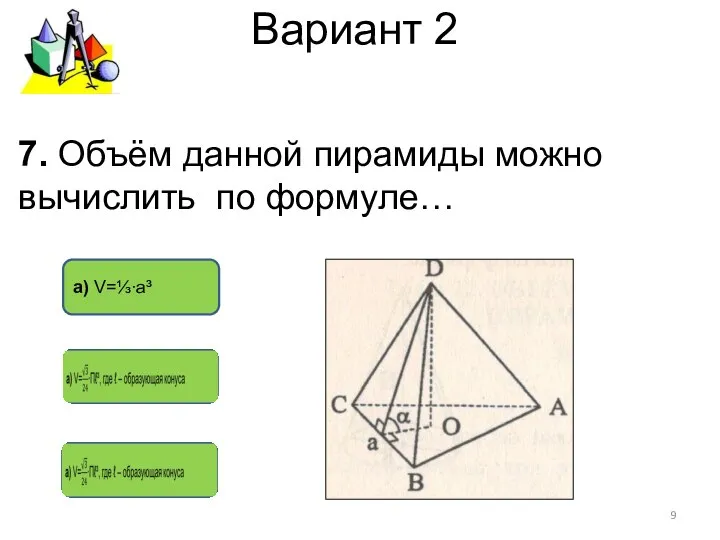
- 9. Вариант 2 а) V=⅓∙а³ 7. Объём данной пирамиды можно вычислить по формуле…
- 10. Вариант 2 8. DАВС- тетраэдр, SАВС=m, SВСD=n, ВС=а,
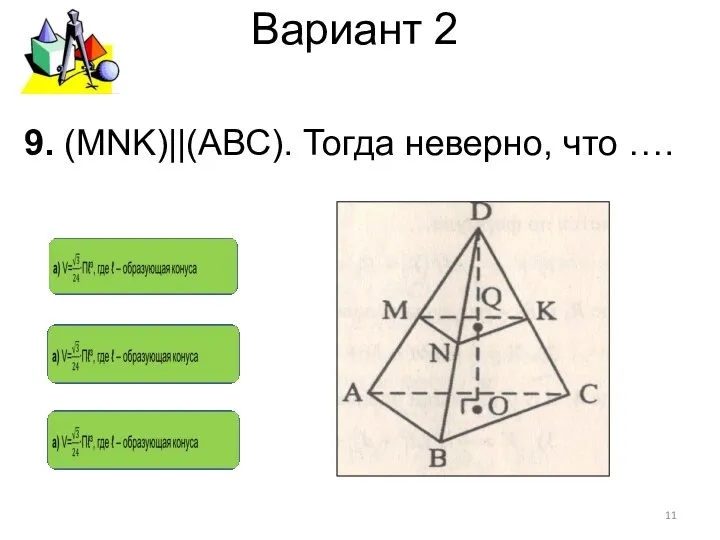
- 11. Вариант 2 9. (MNK)||(АВС). Тогда неверно, что ….
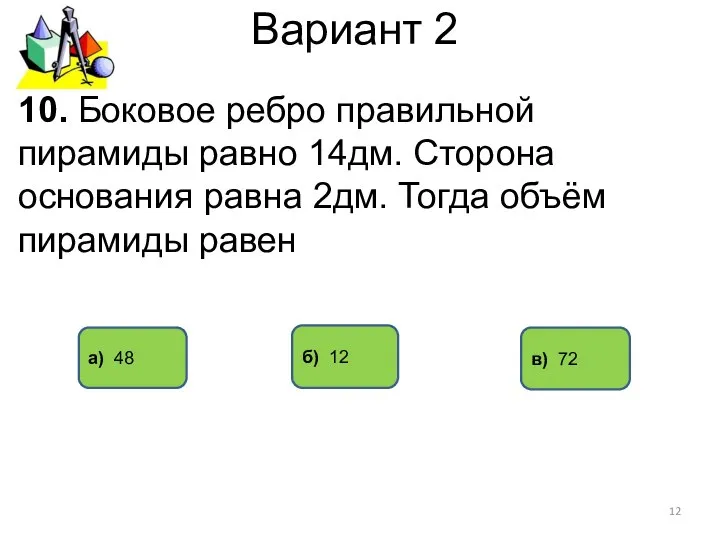
- 12. Вариант 2 а) 48 в) 72 10. Боковое ребро правильной пирамиды равно 14дм. Сторона основания равна
- 13. Вариант 2 а) 48 б) 12 11. Основанием пирамиды служит равнобедренный треугольник со сторонами 10см, 10см
- 14. Вариант 2 б) 96 а) 144 12. Основанием пирамиды является прямоугольный треугольник с катетами 6см и
- 15. Вариант 2 в) 1500П а) 730П б) 1500 13. Высота конуса равна 20см, расстояние от центра
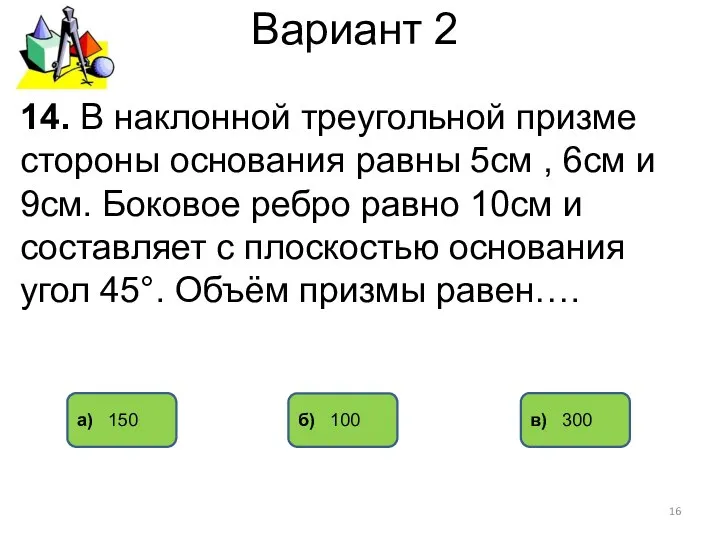
- 16. Вариант 2 а) 150 б) 100 в) 300 14. В наклонной треугольной призме стороны основания равны
- 18. Скачать презентацию





 Деление чисел (часть 1)
Деление чисел (часть 1) Математика. Закрепление изученного материала. 4 класс
Математика. Закрепление изученного материала. 4 класс Дробные числительные
Дробные числительные Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Презентация на тему Деление положительных и отрицательных чисел
Презентация на тему Деление положительных и отрицательных чисел 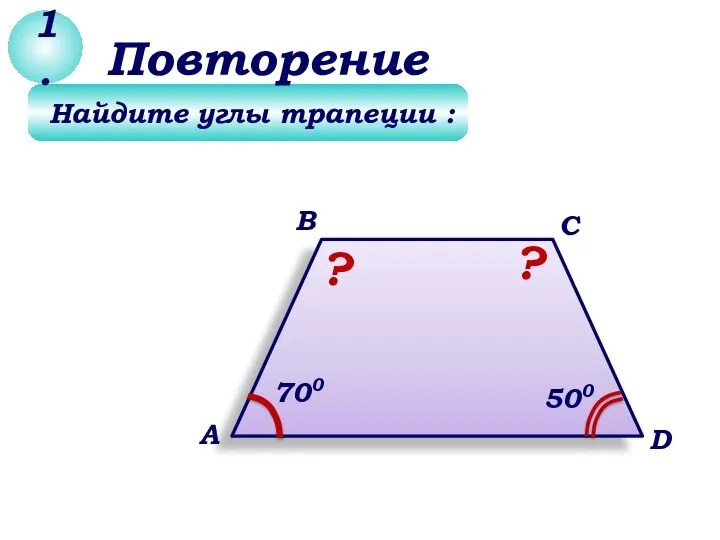 Задачи по геометрия 8 класс
Задачи по геометрия 8 класс Презентация на тему Цифра 3
Презентация на тему Цифра 3  Площадь параллелограмма
Площадь параллелограмма Производная. Тест по алгебре
Производная. Тест по алгебре lecture5
lecture5 Модель чисельності народонаселення
Модель чисельності народонаселення Повторение таблицы умножения. Игра хоккей
Повторение таблицы умножения. Игра хоккей Параллельность в пространстве
Параллельность в пространстве Баскетбол. Математическая викторина
Баскетбол. Математическая викторина Золотое сечение в природе
Золотое сечение в природе Презентация на тему Единицы измерения
Презентация на тему Единицы измерения  Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Симметрия фигур
Симметрия фигур Применение распределительного свойства умножения
Применение распределительного свойства умножения Инструменты для вычислений и измерений. 5 класс
Инструменты для вычислений и измерений. 5 класс Математика ( урок в звуковом сопровождении в полноэкранном режиме)
Математика ( урок в звуковом сопровождении в полноэкранном режиме) Схема Горнера
Схема Горнера Решение уравнений
Решение уравнений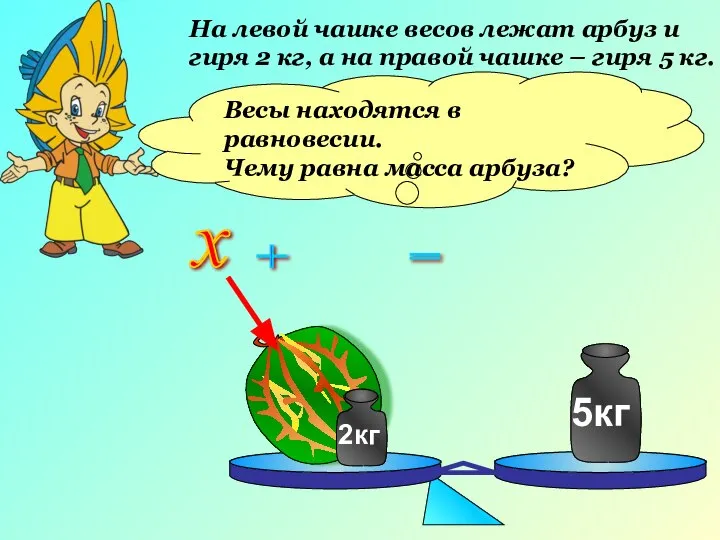 Уравнение. Корень уравнения
Уравнение. Корень уравнения Практическое применение производных
Практическое применение производных Матрицы и действия над ними
Матрицы и действия над ними Теория вероятностей
Теория вероятностей Схема Горнера. Формулы площадей
Схема Горнера. Формулы площадей